Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


8. Gọi số vé loại I và loại II lần lượt là x và y
ĐK: x,y > 0
Tổng số vé bán được là 500 vé `=> x+y=500` (1)
Tổng số tiền vé bán được là 44500000 đồng nên ta có pt:
`100000x+75000y=44500000`
`<=>4x+3y=1780` (2)
Từ (1) và (2) ta có hpt: \(\left\{{}\begin{matrix}x+y=500\\4x+3y=1780\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=280\\y=220\end{matrix}\right.\left(tm\right)\)
Vậy: ...

6. Gọi nhóm bạn trẻ có `x` (người)
ĐK: x ∈ N*
Mỗi người góp số tiền là: \(\dfrac{240}{x}\) (triệu)
Sau khi thêm thì tổng số người có trong nhóm là: \(x+2\) (người)
Sau khi thêm thì mỗi người góp: \(\dfrac{240}{x+2}\) (triệu)
Mà sau khi thêm người thì số tiền góp của mỗi người giảm đi 4 triệu nên ta có pt:
\(\dfrac{240}{x}-4=\dfrac{240}{x+2}\\ \Leftrightarrow\dfrac{240}{x}-\dfrac{240}{x+2}=4\\ \Leftrightarrow\dfrac{240\left(x+2\right)-240x}{x\left(x+2\right)}=4\\ \Leftrightarrow\dfrac{480}{x\left(x+2\right)}=4\\ \Leftrightarrow4x\left(x+2\right)=480\\ \Leftrightarrow x\left(x+2\right)=120\\ \Leftrightarrow x^2+2x-120=0\\ \Leftrightarrow\left(x-10\right)\left(x+12\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=10\left(tm\right)\\x=-12\left(ktm\right)\end{matrix}\right.\)
Vậy: ...

a) R + R' = 5 + 6 = 11 > 18
=> (O) và (O') không giao nhau
b) R + R' = 9 + 3 = 12 > 2
=> (O) và (O') cắt nhau
c) R + R' = 8 + 5 = 13 = OO'
=> (O) và (O') tiếp xúc nhau
d) R + R' = 15 + 4 = 19 > 17
=> (O) và (O') cắt nhau

Bài 2:
\(a.\dfrac{5x-3}{x+2}-4=\dfrac{6}{x+2}\left(x\ne-2\right)\\ \Leftrightarrow\dfrac{5x-3}{x+2}-\dfrac{6}{x+2}=4\\ \Leftrightarrow\dfrac{5x-3-6}{x+2}=4\\ \Leftrightarrow\dfrac{5x-9}{x+2}=4\\ \Leftrightarrow5x-9=4\left(x+2\right)\\ \Leftrightarrow5x-9=4x+8\\ \Leftrightarrow5x-4x=8+9\\ \Leftrightarrow x=17\left(tm\right)\)
\(b.\dfrac{1}{x}-\dfrac{x+2}{x-2}=\dfrac{-2}{x\left(x-2\right)}\left(x\notin\left\{0;2\right\}\right)\\ \Leftrightarrow\dfrac{x-2}{x\left(x-2\right)}-\dfrac{x\left(x+2\right)}{x\left(x-2\right)}=\dfrac{-2}{x\left(x-2\right)}\\ \Leftrightarrow x-2-x\left(x+2\right)=-2\\ \Leftrightarrow x-2-x^2-2x=-2\\ \Leftrightarrow-x^2-x=0\\ \Leftrightarrow x\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
\(c.\dfrac{7}{x-5}-2=\dfrac{3}{5-x}\left(x\ne5\right)\\ \Leftrightarrow\dfrac{7}{x-5}-2-\dfrac{3}{x-5}=0\\ \Leftrightarrow\dfrac{7}{x-5}+\dfrac{3}{x-5}=2\\ \Leftrightarrow\dfrac{10}{x-5}=2\\ \Leftrightarrow x-5=\dfrac{10}{2}=5\\\Leftrightarrow x=5+5\\ \Leftrightarrow x=10\left(tm\right)\)
Bài 3:
a: ĐKXĐ: \(x\notin\left\{-2;2\right\}\)
\(\dfrac{x}{x+2}-\dfrac{x-1}{x-2}=\dfrac{-3x+2}{x^2-4}\)
=>\(\dfrac{x\left(x-2\right)-\left(x-1\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{-3x+2}{\left(x-2\right)\left(x+2\right)}\)
=>\(x^2-2x-\left(x^2+x-2\right)=-3x+2\)
=>-3x+2=-3x+2
=>0x=0(luôn đúng)
Vậy: \(x\in R\backslash\left\{-2;2\right\}\)
b: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{x-1}{x+2}+\dfrac{x+1}{x-2}=\dfrac{2\left(x^2+2\right)}{x^2-4}\)
=>\(\dfrac{\left(x-1\right)\left(x-2\right)+\left(x+1\right)\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{2\left(x^2+2\right)}{x^2-4}\)
=>\(x^2-3x+2+x^2+3x+2-2x^2-4=0\)
=>0x=0(luôn đúng)
vậy: \(x\in R\backslash\left\{2;-2\right\}\)

\(1)-\left(\dfrac{3}{5}+\dfrac{3}{4}\right)-\left(\dfrac{-3}{4}+\dfrac{2}{5}\right)\\ =-\dfrac{3}{5}-\dfrac{3}{4}+\dfrac{3}{4}-\dfrac{2}{5}\\ =\left(\dfrac{3}{4}-\dfrac{3}{4}\right)+\left(-\dfrac{3}{5}-\dfrac{2}{5}\right)\\ =-1\\ 2)-\left(\dfrac{3}{7}+\dfrac{3}{8}\right)-\left(-\dfrac{3}{8}+\dfrac{4}{7}\right)\\ =-\dfrac{3}{7}-\dfrac{3}{8}+\dfrac{3}{8}-\dfrac{4}{7}\\ =\left(\dfrac{3}{8}-\dfrac{3}{8}\right)+\left(-\dfrac{3}{7}-\dfrac{4}{7}\right)\\ =-1\\ 3)\left(\dfrac{-25}{27}-\dfrac{31}{42}\right)-\left(\dfrac{-7}{27}-\dfrac{3}{42}\right)\\ =-\dfrac{25}{27}-\dfrac{31}{42}+\dfrac{7}{27}+\dfrac{3}{42}\\ =\left(\dfrac{-25}{27}+\dfrac{7}{27}\right)+\left(\dfrac{-31}{42}+\dfrac{3}{42}\right)\\ =\dfrac{-18}{27}+\dfrac{-28}{42}\\ =\dfrac{-2}{3}+\dfrac{-2}{3}\\ =-\dfrac{4}{3}\)
Bài 17:
4: \(\left(-\dfrac{1}{2}+\dfrac{7}{6}\right)-\left(-\dfrac{5}{2}+\dfrac{1}{6}\right)\)
\(=-\dfrac{1}{2}+\dfrac{7}{6}+\dfrac{5}{2}-\dfrac{1}{6}\)
=2-1=1
5: \(\left(\dfrac{16}{21}+\dfrac{27}{12}\right)-\left(\dfrac{14}{12}-\dfrac{5}{21}\right)\)
\(=\dfrac{16}{21}+\dfrac{27}{12}-\dfrac{14}{12}+\dfrac{5}{21}\)
\(=1-\dfrac{13}{12}=-\dfrac{1}{12}\)
6: \(\left(\dfrac{13}{23}+\dfrac{-15}{4}\right)+\left(\dfrac{10}{23}-\dfrac{1}{4}\right)\)
\(=\dfrac{13}{23}+\dfrac{10}{23}-\dfrac{15}{4}-\dfrac{1}{4}\)
\(=1-4=-3\)
Bài 18:
1: \(6\dfrac{2}{5}-\left(2\dfrac{4}{9}+4\dfrac{2}{5}\right)\)
\(=6+\dfrac{2}{5}-2-\dfrac{4}{9}-4-\dfrac{2}{5}\)
\(=-\dfrac{4}{9}\)
2: \(7\dfrac{3}{5}-\left(2\dfrac{5}{7}+5\dfrac{3}{5}\right)\)
\(=7+\dfrac{3}{5}-2-\dfrac{5}{7}-5-\dfrac{3}{5}\)
\(=-\dfrac{5}{7}\)
3: \(8\dfrac{2}{7}-\left(3\dfrac{4}{9}+4\dfrac{2}{7}\right)\)
\(=8+\dfrac{2}{7}-3-\dfrac{4}{9}-4-\dfrac{2}{7}\)
\(=1-\dfrac{4}{9}=\dfrac{5}{9}\)
4: \(8\dfrac{2}{9}-\left(4\dfrac{2}{9}-5\dfrac{1}{2}\right)\)
\(=8+\dfrac{2}{9}-4-\dfrac{2}{9}+5+\dfrac{1}{2}\)
\(=9+\dfrac{1}{2}=\dfrac{19}{2}\)
5: \(21\dfrac{4}{11}-\left(1\dfrac{3}{5}+7\dfrac{4}{11}\right)\)
\(=21+\dfrac{4}{11}-1-\dfrac{3}{5}-7-\dfrac{4}{11}\)
\(=13-\dfrac{3}{5}=\dfrac{62}{5}\)
6: \(11\dfrac{3}{13}-\left(2\dfrac{4}{7}+5\dfrac{3}{13}\right)\)
\(=11+\dfrac{3}{13}-2-\dfrac{4}{7}-5-\dfrac{3}{13}\)
\(=4-\dfrac{4}{7}=\dfrac{24}{7}\)
7: \(\left(6\dfrac{4}{9}+3\dfrac{7}{11}\right)-4\dfrac{4}{9}\)
\(=6+\dfrac{4}{9}+3+\dfrac{7}{11}-4-\dfrac{4}{9}\)
\(=5+\dfrac{7}{11}=\dfrac{62}{11}\)
8: \(\left(7\dfrac{8}{9}+2\dfrac{3}{13}\right)-4\dfrac{8}{9}\)
\(=7+\dfrac{8}{9}+2+\dfrac{3}{13}-4-\dfrac{8}{9}\)
\(=5+\dfrac{3}{13}=\dfrac{68}{13}\)
9: \(\left(6\dfrac{5}{7}+2\dfrac{7}{9}\right)-4\dfrac{5}{7}\)
\(=6+\dfrac{5}{7}+2+\dfrac{7}{9}-4-\dfrac{5}{7}\)
\(=4+\dfrac{7}{9}=\dfrac{43}{9}\)

\(\left(8+2\dfrac{1}{3}-\dfrac{3}{5}\right):\left(5-\dfrac{1}{4}-\dfrac{5}{8}\right)\\ =\left(8+2+\dfrac{1}{3}-\dfrac{3}{5}\right):\left(5-\dfrac{2}{8}-\dfrac{5}{8}\right)\\ =\left(10+\dfrac{1}{3}-\dfrac{3}{5}\right):\left(5-\dfrac{7}{8}\right)\\ =\left(\dfrac{150}{15}+\dfrac{5}{15}-\dfrac{9}{15}\right):\left(\dfrac{40}{8}-\dfrac{7}{8}\right)\\ =\dfrac{146}{15}:\dfrac{33}{8}\\ =\dfrac{146}{15}\cdot\dfrac{8}{33}\\ =\dfrac{1168}{495}\)

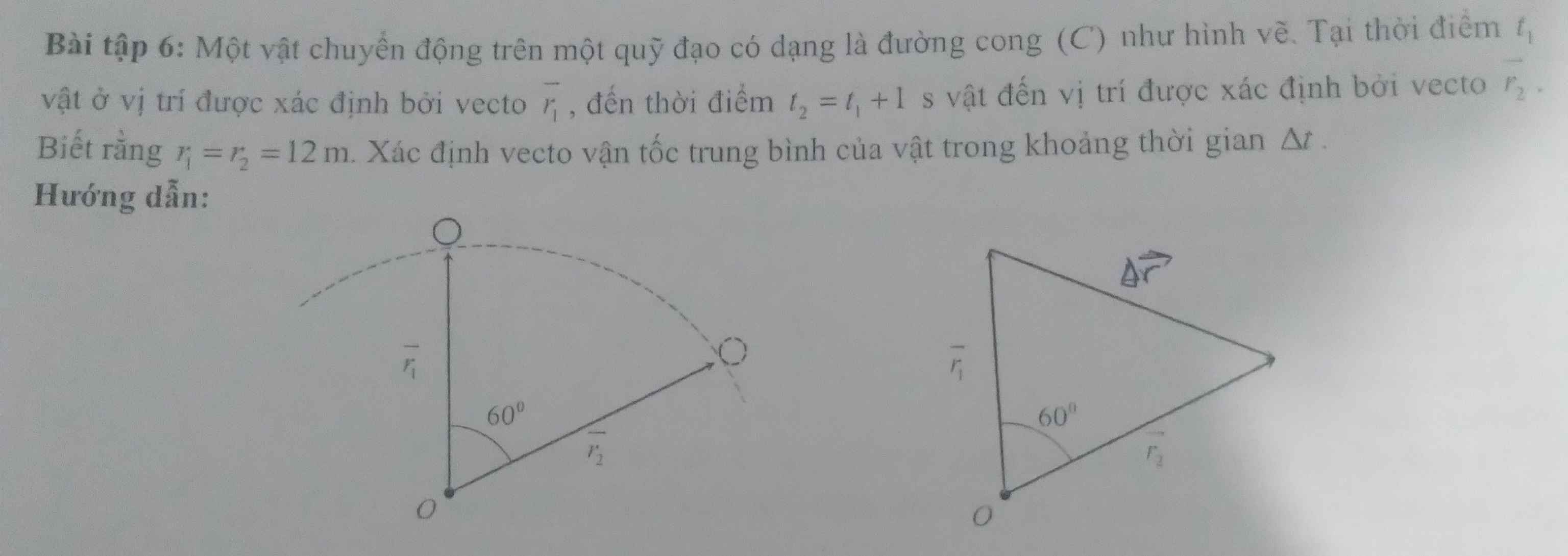
Vectơ vận tốc trung bình có phương và chiều trùng với vectơ độ dời

Độ lớn của vận tốc trung bình được tính như sau:
$|\overrightarrow{v_{tb}}|=\dfrac{|\overrightarrow{\Delta r}|}{\Delta t}=\dfrac{12}{1}=12$ (m/s)
(Do tam giác tạo bởi các vectơ $\overrightarrow{r_1},\,\overrightarrow{r_2},\,\overrightarrow{\Delta r}$ đều)

\(f\left(x\right)+g\left(x\right)=x^2h\left(x\right)\)
\(2x^3-3x^2+3x+1+g\left(x\right)=x^2\left(2x+1\right)\)
\(g\left(x\right)=2x^3+x^2-2x^3+3x^2-3x-1=4x^2-3x-1\)
chọn C
`#3107.101107`
Ta có:
`f(x) + g(x) = x^2h(x)`
`\Rightarrow g(x) = x^2h(x) - f(x)`
`g(x) = x^2 * (2x + 1) - (2x^3 - 3x^2 + 3x + 1)`
`= 2x^3 + x^2 - 2x^3 + 3x^2 - 3x - 1`
`= 4x^2 - 3x - 1`
Chọn C.

Bài 3:
1; A = 1 + 2 + 3 + ... + 2023 + 2024
Dãy số trên là dãy số cách đều với khoảng cách là: 2 - 1 = 1
Số số hạng của dãy số trên là: (2024 - 1) : 1 + 1 = 2024
Tổng của dãy số trên là: (2024 + 1) x 2024 : 2 = 2049300
Đáp số:....
BÀi 3:
2; B = 1 + 3 + 5 + ... + 2023 + 2025
Xét dãy số: 1; 3; 5;...; 2023; 2025
Dãy số trên là dãy số cách đều với khoảng cách là:
3 - 1 = 2
Số số hạng của dãy số trên là: (2025 - 1) : 2 + 1 = 1013
Tổng của dãy số trên là: (2025 + 1) x 1013 : 2 = 1026196



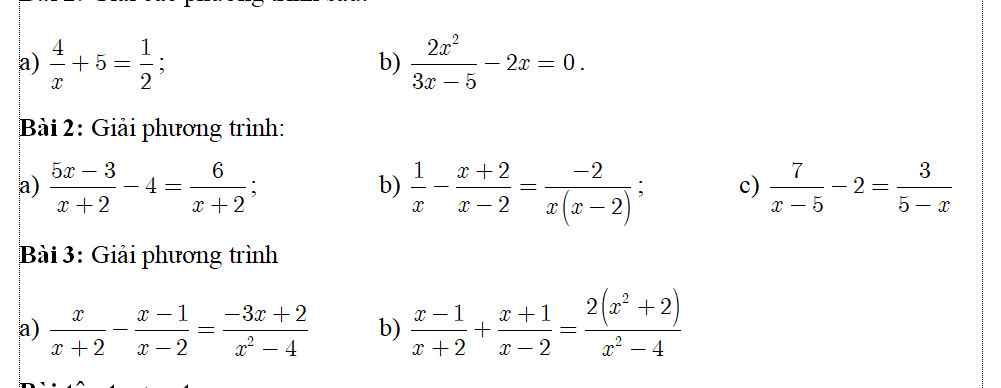
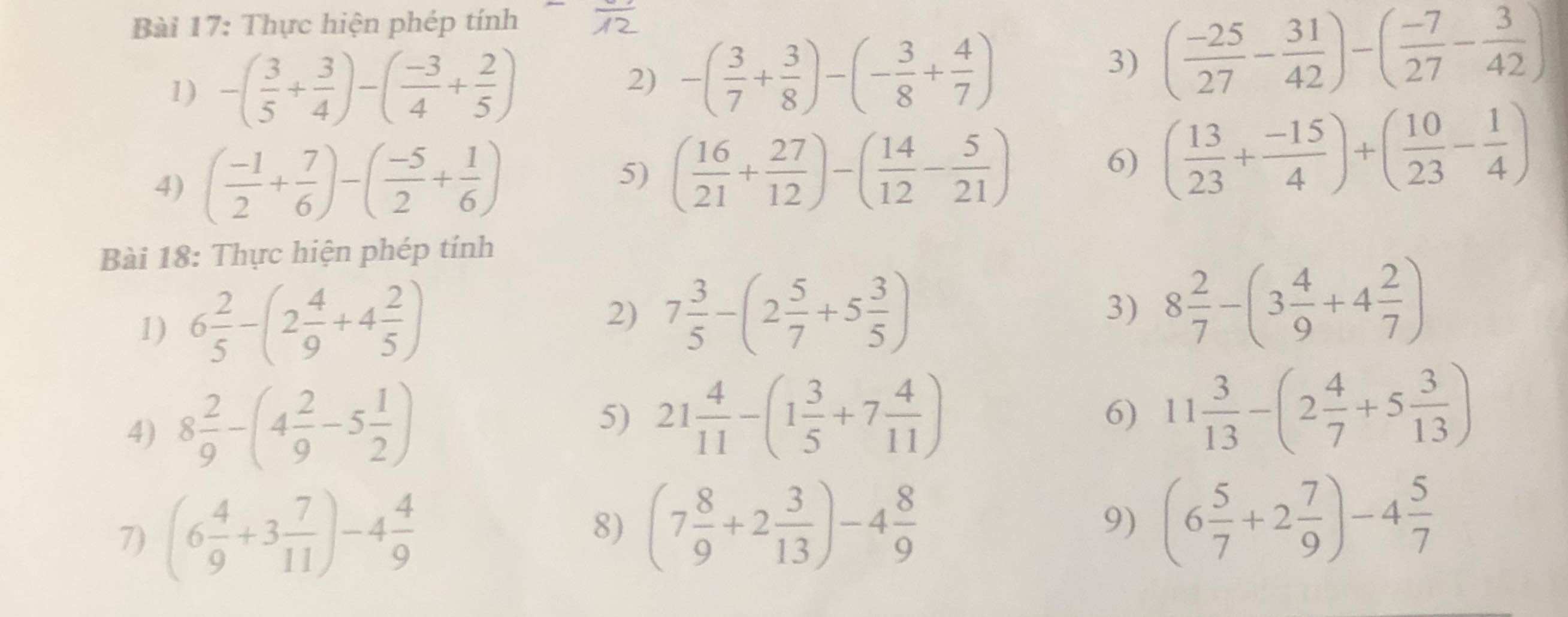
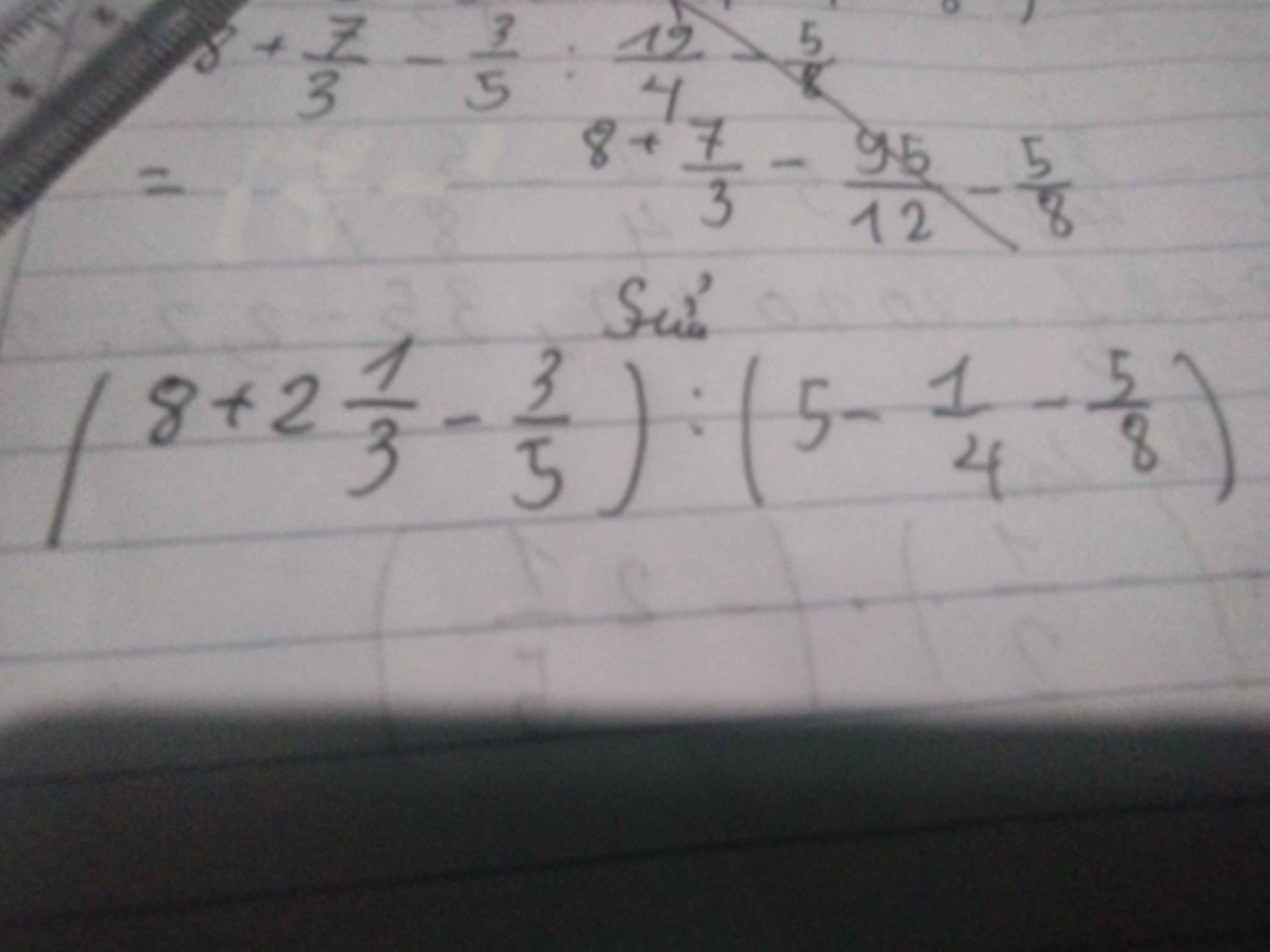
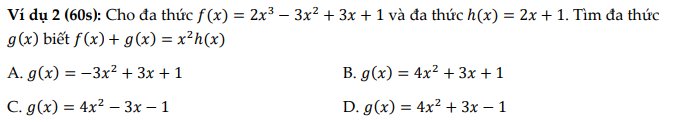

\(a)\dfrac{5}{x+7}=\dfrac{-14}{x-5}\left(x\ne-7;x\ne5\right)\\ \Leftrightarrow-14\left(x+7\right)=5\left(x-5\right)\\ \Leftrightarrow-14x-98=5x-25\\ \Leftrightarrow5x+14x=-98+25\\ \Leftrightarrow19x=-73\\ \Leftrightarrow x=-\dfrac{73}{19}\left(tm\right)\\ b)\dfrac{3}{3x-2}=\dfrac{1}{x+1}\left(x\ne\dfrac{2}{3};x\ne-1\right)\\ \Leftrightarrow3\left(x+1\right)=3x-2\\ \Leftrightarrow3x+3=3x-2\\ \Leftrightarrow3=-2\)
=> Pt vô nghiệm
\(c)\dfrac{x}{x-2}=\dfrac{1}{x+1}+1\left(x\ne2;x\ne-1\right)\\ \Leftrightarrow\dfrac{x}{x-2}=\dfrac{x+2}{x+1}\\ \Leftrightarrow x\left(x+1\right)=\left(x-2\right)\left(x+2\right)\\ \Leftrightarrow x^2+x=x^2-4\\ \Leftrightarrow x=-4\left(tm\right)\)
\(d)\dfrac{x+6}{x+5}+\dfrac{3}{2}=2\left(x\ne-5\right)\\ \Leftrightarrow\dfrac{2\left(x+6\right)}{2\left(x+5\right)}+\dfrac{3\left(x+5\right)}{2\left(x+5\right)}=2\\ \Leftrightarrow\dfrac{2\left(x+6\right)+3\left(x+5\right)}{2\left(x+5\right)}=2\\ \Leftrightarrow2x+12+3x+15=4\left(x+5\right)\\ \Leftrightarrow5x+27=4x+20\\ \Leftrightarrow5x-4x=20-27\\ \Leftrightarrow x=-7\left(tm\right)\)
e: ĐKXĐ: x<>3
\(\dfrac{x+5}{x-3}+2=\dfrac{2}{x-3}\)
=>\(\dfrac{x+5+2x-6}{x-3}=\dfrac{2}{x-3}\)
=>3x-1=2
=>3x=3
=>x=1(nhận)
f: ĐKXĐ: \(x\notin\left\{0;-1\right\}\)
\(\dfrac{3x+5}{x+1}+\dfrac{2}{x}=3\)
=>\(\dfrac{3x+3+2}{x+1}+\dfrac{2}{x}=3\)
=>\(\dfrac{2}{x+1}+\dfrac{2}{x}=0\)
=>\(\dfrac{2x+2x+2}{x\left(x+1\right)}=0\)
=>4x+2=0
=>4x=-2
=>\(x=-\dfrac{1}{2}\left(loại\right)\)
g: ĐKXĐ: \(x\notin\left\{3;2\right\}\)
\(\dfrac{x+3}{x-2}+\dfrac{x+2}{x-3}=2\)
=>\(\dfrac{\left(x+3\right)\left(x-3\right)+\left(x+2\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}=2\)
=>\(\dfrac{x^2-9+x^2-4}{x^2-5x+6}=2\)
=>\(2\left(x^2-5x+6\right)=2x^2-13\)
=>-10x+12=-13
=>-10x=-25
=>\(x=\dfrac{5}{2}\left(nhận\right)\)
h: ĐKXĐ: \(x\notin\left\{2;3\right\}\)
\(\dfrac{2}{x-2}-\dfrac{3}{x-3}=\dfrac{3x-20}{\left(x-3\right)\left(x-2\right)}\)
=>\(\dfrac{2\left(x-3\right)-3\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}=\dfrac{3x-20}{\left(x-3\right)\left(x-2\right)}\)
=>\(2x-6-3x+6=3x-20\)
=>3x-20=-x
=>4x=20
=>x=5(nhận)