:}

hog bic lm=))

 Cách 1 (đồ thị): Đầu tiên ta xác định miền nghiệm của hệ bất phương trình sau: \(\left\{{}\begin{matrix}x>0\\y>0\\\dfrac{x}{3}+\dfrac{y}{4}\le1\end{matrix}\right.\) như sau:

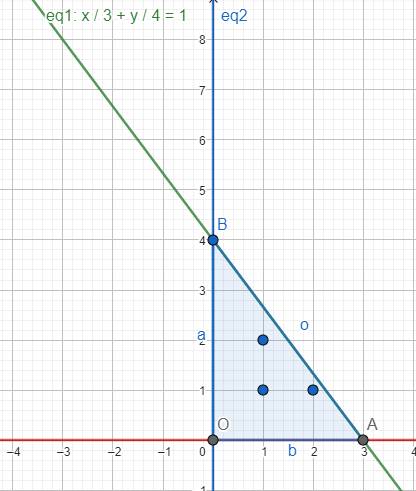
 Sau đó ta tìm tất cả các điểm nguyên nằm ở miền trong tam giác OAB. Ta nhận thấy các điểm này là \(\left(1,1\right);\left(1,2\right);\left(2,1\right)\). Vậy các nghiệm (x; y) của bpt là \(\left(1;1\right),\left(1;2\right),\left(2;1\right)\)

Cách 2: (đại số)

 Ta có \(\dfrac{x}{3}+\dfrac{y}{4}\le1\)  nên \(\dfrac{x}{3}< 1\) \(\Leftrightarrow x< 3\) \(\Rightarrow x\in\left\{1,2\right\}\)

\(\dfrac{y}{4}< 1\Rightarrow y< 4\Rightarrow y\in\left\{1,2,3\right\}\)

 Thử lại, ta thấy chỉ có các cặp \(\left(x;y\right)=\left(1;1\right),\left(1;2\right),\left(2;1\right)\) là thỏa mãn. Vậy...

Trước hết ta chứng minh bổ đề sau:

Bổ đề 1: Cho tam giác ABC và 1 điểm M trên cạnh BC. Khi đó: \(\overrightarrow{AM}=\dfrac{MC}{BC}\overrightarrow{AB}+\dfrac{MB}{BC}\overrightarrow{AC}\)

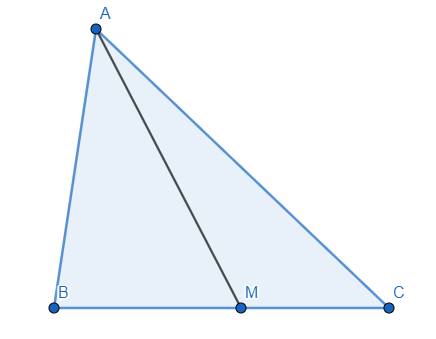
Thật vậy, ta có \(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)

\(=\overrightarrow{AB}+\dfrac{BM}{BC}\overrightarrow{BC}\)

\(=\overrightarrow{AB}+\dfrac{BM}{BC}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)

\(=\left(1-\dfrac{BM}{BC}\overrightarrow{AB}\right)+\dfrac{BM}{BC}\overrightarrow{AC}\)

\(=\dfrac{CM}{BC}\overrightarrow{AB}+\dfrac{BM}{BC}\overrightarrow{AC}\), bổ đề 1 được chứng minh.

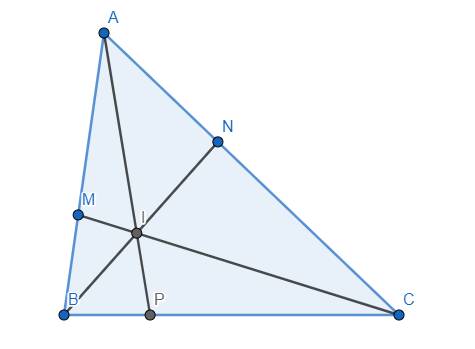
Gọi P là giao điểm của AI và BC. Ta có: 

\(\dfrac{MA}{MB}.\dfrac{PB}{PC}.\dfrac{NC}{NA}=1\) \(\Rightarrow x.\dfrac{PB}{PC}.\dfrac{1}{y}=1\) \(\Rightarrow\dfrac{PB}{PC}=\dfrac{y}{x}\) \(\Rightarrow\dfrac{CP}{CB}=\dfrac{x}{x+y}\)

Mặt khác, \(\dfrac{IP}{IA}.\dfrac{MA}{MB}.\dfrac{CB}{CP}=1\) \(\Rightarrow\dfrac{IP}{IA}.x.\dfrac{x+y}{x}=1\) \(\Rightarrow\dfrac{IP}{IA}=\dfrac{1}{x+y}\)

Do đó \(\overrightarrow{AI}=\left(x+y\right)\overrightarrow{IP}\)

Mà theo bổ đề 1: \(\overrightarrow{IP}=\dfrac{PC}{BC}\overrightarrow{IB}+\dfrac{PB}{BC}\overrightarrow{IC}\)

\(=\dfrac{x}{x+y}\overrightarrow{IB}+\dfrac{y}{x+y}\overrightarrow{IC}\)

\(\Rightarrow\overrightarrow{AI}=x\overrightarrow{IB}+y\overrightarrow{IC}\) (đpcm)

\(VT=\cos^2a-2.\dfrac{1}{2}\left[\cos\left(a+b\right)+\cos\left(a-b\right)\right].\cos\left(a+b\right)+\cos^2\left(a+b\right)=\)

\(=\cos^2a-\cos^2\left(a+b\right)-\cos\left(a+b\right)\cos\left(a-b\right)+\cos^2\left(a+b\right)=\)

\(=\cos^2a-\dfrac{1}{2}\left(\cos2a+\cos2b\right)=\)

\(=\dfrac{2\cos^2a-\cos^2a+\sin^2a-1+2\sin^2b}{2}=\)

\(=\dfrac{\left(\cos^2a+\sin^2a\right)-1+2\sin^2b}{2}=\sin^2b=VP\)

cos²a - cos (a+b) (2 cosa . cosb - cos (a+b) = sin²b

Cos²a - ( cos a.cosb- sina .sinb)( 2 cosa .cosb - ( cosa .cosb - sina .sinb) = sin²b

cos²a - (cosa.cosb - sina.sinb) (cosa.cosb + sina .sinb) = sin²b

cos²a - ( cos²a . cos²b - sin²a .sin²b = sin²b ) .

         1 - sin²a  - ( 1 - sin²a ) ( 1 - sin²b) - sin²a .sin²b  = sin²b

         1 - sin²a - ( 1- sin²b  - sin²a  + sin²a .sin²b  - sin² a .sin²b = sin²b

         1 - sin²a -1  + sin² b + sin²a  = sin²b   

                     Sin²b  = Sin²b   điều đã CM

`A=[sin x+sin 2x+sin 3x]/[cos x+cos 2x+cos 3x]`

`A=[(sin x+sin 3x)+sin 2x]/[(cos x+cos 3x)+cos 2x]`

`A=[2sin 2x.cos (-x)+sin 2x]/[2cos 2x.cos (-x)+cos 2x]`

`A=[sin 2x(2cos(-x)+1)]/[cos 2x(2cos(-x)+1)]`

`A=[sin 2x]/[cos 2x]=tan 2x`.