
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực


Đặt \(z=x+yi\)
\(\Rightarrow\left(2-i\right)\left(x-yi\right)+\left(4+3i\right)\left(x+yi\right)=7-4i\)
\(\Leftrightarrow2x-y-\left(x+2y\right)i+4x-3y+\left(3x+4y\right)i=7-4i\)
\(\Leftrightarrow6x-4y+\left(2x+2y\right)i=7-4i\)
\(\Rightarrow\left\{{}\begin{matrix}6x-4y=7\\2x+2y=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{10}\\y=-\dfrac{19}{10}\end{matrix}\right.\)
\(\Rightarrow z=-\dfrac{1}{10}-\dfrac{19}{10}i\)

Không gian mẫu: \(C_{12}^4\)
- Chọn 4 lớp có số thứ tự liên tiếp nhau: có 9 cách
- Chọn 4 lớp trong đó có 3 lớp liên tiếp và 1 lớp không liên tiếp với 3 lớp còn lại:
Chọn bộ 3 số liên tiếp: có 10 cách
+ 3 lớp liên tiếp nhau là 123 hoặc 10-11-12: chọn lớp còn lại có 8 cách \(\Rightarrow2.8=16\) cách
+ 8 trường hợp còn lại mỗi trường hợp có 7 cách chọn \(\Rightarrow7.8=56\) cách
\(\Rightarrow9+16+56=81\) cách
Xác suất: \(P=\dfrac{81}{C_{12}^4}=\dfrac{9}{55}\)

Đặt \(3^x=t>0\Rightarrow t^2-2\left(7-x\right)t+45-18x=0\)
\(\Delta'=\left(7-x\right)^2-\left(45-18x\right)=\left(x+2\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}t=7-x+x+2=9\\t=7-x-\left(x+2\right)=5-2x\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}3^x=9\Rightarrow x=2\\3^x=5-2x\left(1\right)\end{matrix}\right.\)
Xét (1) \(\Leftrightarrow3^x+2x-5=0\)
Nhận thấy \(x=1\) là 1 nghiệm của (1)
Xét hàm \(f\left(x\right)=3^x+2x-5\Rightarrow f'\left(x\right)=3^x.ln3+2>0;\forall x\)
\(\Rightarrow f\left(x\right)\) đồng biến trên R nên \(f\left(x\right)\) có tối đa 1 nghiệm
\(\Rightarrow x=1\) là nghiệm duy nhất của (1)
Vậy pt đã cho có 2 nghiệm thực \(x=\left\{1;2\right\}\)

\(y'=x^2-mx+2m=0\) (1)
Hàm nghịch biến trên một đoạn có độ dài bằng 3 khi và chỉ khi:
\(\left\{{}\begin{matrix}\Delta=m^2-8m>0\\\left|x_1-x_2\right|=3\\\end{matrix}\right.\) trong đó \(x_1;x_2\) là 2 nghiệm của (1)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>8\end{matrix}\right.\\\left(x_1+x_2\right)^2-4x_1x_2=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>8\end{matrix}\right.\\m^2-8m=9\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=-1\\m=9\end{matrix}\right.\)
(1)
Hàm nghịch biến trên một đoạn có độ dài bằng 3 khi và chỉ khi:
trong đó là 2 nghiệm của (1)

Xét \(I=\int\limits^1_0x.f\left(3x\right)dx\)
Đặt \(3x=u\Rightarrow dx=\dfrac{1}{3}du\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow u=0\\x=1\Rightarrow u=3\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{1}{9}\int\limits^3_0u.f\left(u\right)du=\dfrac{1}{9}\int\limits^3_0x.f\left(x\right)dx=1\)
\(\Rightarrow J=\int\limits^3_0x.f\left(x\right)dx=9\)
Xét J, đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=x.dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=\dfrac{x^2}{2}\end{matrix}\right.\)
\(\Rightarrow J=\dfrac{x^2}{2}.f\left(x\right)|^3_0-\dfrac{1}{2}\int\limits^3_0x^2.f'\left(x\right)dx=\dfrac{9}{2}-\dfrac{1}{2}\int\limits^3_0x^2.f'\left(x\right)dx\)
\(\Rightarrow\int\limits^3_0x^2.f'\left(x\right)dx=9-2J=-9\)

Mỗi lần đi qua bên kia sông thì trên đò phải có 1 người và 1 quỷ. Tức là 1 người đi sang sông thì chở theo 1 quỷ đi.


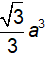
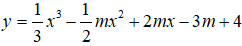
Gọi tọa độ các điểm A; B; C lần lượt là \(A\left(a;0;0\right);B\left(0;b;0\right);C\left(0;0;c\right)\) với \(a;b;c>0\)
Phương trình (P) theo đoạn chắn:
\(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{c}{z}=1\) (1)
Do (P) qua M nên: \(\dfrac{1}{a}+\dfrac{2}{b}+\dfrac{3}{c}=1\)
ÁP dụng BĐT Cô-si:
\(1=\dfrac{1}{a}+\dfrac{2}{b}+\dfrac{3}{c}\ge3\sqrt[3]{\dfrac{6}{abc}}\Rightarrow abc\ge162\)
\(\Rightarrow V_{OABC}=\dfrac{1}{6}abc=27\)
Dấu "=" xảy ra khi \(\dfrac{1}{a}=\dfrac{2}{b}=\dfrac{3}{c}\Rightarrow\left\{{}\begin{matrix}b=2a\\c=3a\end{matrix}\right.\)
\(\Rightarrow\dfrac{1}{a}+\dfrac{2}{2a}+\dfrac{3}{3a}=1\Rightarrow a=3\Rightarrow b=6;c=9\)
Thế vào (1): \(\dfrac{x}{3}+\dfrac{y}{6}+\dfrac{z}{9}=1\Leftrightarrow6x+3y+2z-18=0\)