cho hai số có tổng là 140.Biết 3/5 số thứ nhất thì hơn 1/4 số thứ 2 là 33 đơn vị tìm hai số đó?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a. Áp dụng định lý Pitago:
$AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=8$
$AH=2S_{ABC}:BC=AB.AC:BC=6.8:10=4,8$
b.
Xét tam giác $AEH$ và $AHB$ có:
$\widehat{A}$ chung
$\widehat{AEH}=\widehat{AHB}=90^0$
$\Rightarrow \triangle AEH\sim \triangle AHB$ (g.g)
$\Rightarrow \frac{AE}{AH}=\frac{AH}{AB}$
$\Rightarrow AH^2=AE.AB(1)$
Hoàn toàn tương tự: $\triangle AFH\sim \triangle AHC$
$\Rightarrow AH^2=AF.AC(2)$
Từ $(1); (2)\Rightarrow AE.AB=AF.AC$
c.
$HE\perp AB, AB\perp AC$ nên $HE\parallel AC$
Tam giác vuông $BEH$ vuông tại $E$ có trung tuyến $EM$ ứng với cạnh huyền $BH$
nên $EM=\frac{BH}{2}=MH$
$\Rightarrow EMH$ cân tại $M$
$\Rightarrow \widehat{MEH}=\widehat{MHE}=\widehat{HCA}(3)$ (2 góc đồng vị)
Tứ giác $AEHF$ có 3 góc $\widehat{A}=\widehat{E}=\widehat{F}=90^0$ nên là hcn.
$\Rightarrow \widehat{HEF}=\widehat{HAF}=\widehat{HAC}(4)$
Từ $(3); (4)\Rightarrow \widehat{MEH}+\widehat{HEF}=\widehat{HCA}+\widehat{HAC}$
$\Rightarrow \widehat{MEF}=\widehat{HCA}+\widehat{HAC}=90^0$
$\Rightarrow EM\perp EF$


`#3107.101107`
`g)`
\(\dfrac{4}{19}\cdot\dfrac{-3}{7}+\dfrac{-3}{7}\cdot\dfrac{15}{19}+\dfrac{5}{7}\)
\(=\dfrac{-3}{7}\left(\dfrac{4}{19}+\dfrac{15}{19}\right)+\dfrac{5}{7}\)
\(=\dfrac{-3}{7}\cdot1+\dfrac{5}{7}\)
\(=-\dfrac{3}{7}+\dfrac{5}{7}=\dfrac{2}{7}\)
`h)`
\(\dfrac{5}{9}\cdot\dfrac{7}{13}+\dfrac{5}{9}\cdot\dfrac{9}{13}-\dfrac{5}{9}\cdot\dfrac{3}{13}\)
\(=\dfrac{5}{9}\cdot\left(\dfrac{7}{13}+\dfrac{9}{13}-\dfrac{3}{13}\right)\)
\(=\dfrac{5}{9}\cdot\left(\dfrac{7+9-3}{13}\right)\)
\(=\dfrac{5}{9}\cdot1=\dfrac{5}{9}\)
`i)`
\(\left(\dfrac{-4}{5}+\dfrac{4}{3}\right)+\left(\dfrac{-5}{4}+\dfrac{14}{5}\right)-\dfrac{7}{3}\)
\(=\dfrac{-4}{5}+\dfrac{4}{3}+\dfrac{-5}{4}+\dfrac{14}{5}-\dfrac{7}{3}\)
\(=\left(-\dfrac{4}{5}+\dfrac{14}{5}\right)+\left(\dfrac{4}{3}-\dfrac{7}{3}\right)-\dfrac{5}{4}\)
\(=\dfrac{10}{5}+\dfrac{-3}{3}-\dfrac{5}{4}\)
\(=2-1-\dfrac{5}{4}\)
\(=1-\dfrac{5}{4}\)
\(=-\dfrac{1}{4}\)
`j)`
\(\dfrac{8}{3}\cdot\dfrac{2}{5}\cdot\dfrac{3}{8}\cdot10\cdot\dfrac{19}{92}\)
\(=\left(\dfrac{8}{3}\cdot\dfrac{3}{8}\right)\cdot\left(\dfrac{2}{5}\cdot10\right)\cdot\dfrac{19}{92}\)
\(=1\cdot\dfrac{20}{5}\cdot\dfrac{19}{92}\)
\(=4\cdot\dfrac{19}{92}=\dfrac{19}{23}\)
`k)`
\(\dfrac{-5}{7}\cdot\dfrac{2}{11}+\dfrac{-5}{7}\cdot\dfrac{9}{14}+1\dfrac{5}{7}\)
\(=-\dfrac{5}{7}\cdot\dfrac{2}{11}-\dfrac{5}{7}\cdot\dfrac{9}{14}+1+\dfrac{5}{7}\)
\(=\dfrac{5}{7}\cdot\left(-\dfrac{2}{11}-\dfrac{9}{14}+1\right)+1\)
\(=\dfrac{5}{7}\cdot\dfrac{27}{154}+1\)
\(=\dfrac{135}{1078}+1=\dfrac{1213}{1078}\)
`l)`
\(\dfrac{12}{19}\cdot\dfrac{7}{15}\cdot\dfrac{-13}{17}\cdot\dfrac{19}{12}\cdot\dfrac{17}{13}\)
\(=\left(\dfrac{12}{19}\cdot\dfrac{19}{12}\right)\cdot\left(-\dfrac{13}{17}\cdot\dfrac{17}{13}\right)\cdot\dfrac{7}{15}\)
\(=1\cdot\left(-1\right)\cdot\dfrac{7}{15}=-\dfrac{7}{15}\)
mng ơi cho em hỏi ạ .ngoài làm bài tập đứng top 1,2,3 để nhận xu ra thì còn cách nào để nhân xu ko ạ


Em tham khảo nhé
1. Because learning English helps me speak fluently and communicate well with foreigners.
2. When communicating with foreigners, I feel very happy and comfortable. Because thanks to that, I can understand more about the culture, customs and rituals, and most of all, I can bring Vietnam closer to friends in the international arena.
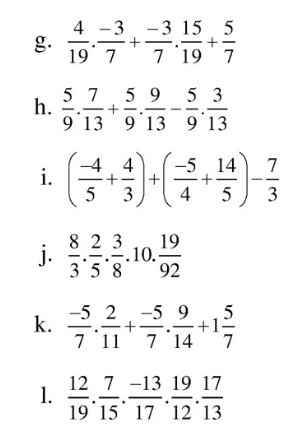
Đây là dạng toán nâng cao chuyên đề toán hai tỉ số, cấu trúc thi chuyên thi học sinh giỏi các cấp, thi violympic. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng sơ đồ như sau:
Giải:
\(\dfrac{3}{5}\) số thứ nhất và \(\dfrac{3}{5}\) số thứ hai là: 140 x \(\dfrac{3}{5}\) = 84
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
\(\dfrac{1}{4}\) số thứ hai và \(\dfrac{3}{5}\) số thứ hai là: 84 - 33 = 51
51 ứng với: \(\dfrac{1}{4}\) + \(\dfrac{3}{5}\) = \(\dfrac{17}{20}\) (số thứ hai)
Số thứ hai là: 51 : \(\dfrac{17}{20}\) = 60
Số thứ nhất là: 140 - 60 = 80
Đáp số: số thứ nhất 80
số thứ hai 60
Lời giải:
Gọi số thứ nhất là $a$ và số thứ hai là $b$. Theo bài ra ta có:
$a+b=140$
$a=140-b$
$\frac{3}{5}\times a-\frac{1}{4}\times b=33$
Thay $a=140-b$ vào điều kiện trên thì:
$\frac{3}{5}\times (140-b)-\frac{1}{4}\times b=33$
$84-\frac{3}{5}\times b-\frac{1}{4}\times b=33$
$84-b\times (\frac{3}{5}+\frac{1}{4})=33$
$84-b\times \frac{17}{20}=33$
$b\times \frac{17}{20}=84-33=51$
$b=51:\frac{17}{20}=60$
$a=140-b=140-60=80$
Vậy hai số cần tìm là $80$ và $60$