Lời giải:

$a+9\vdots 6; b+2011\vdots 6$

$\Rightarrow a+9+b+2011\vdots 6$

$\Rightarrow a+b+2020\vdots 6$

$\Rightarrow a+b+4+336.6\vdots 6$

$\Rightarrow a+b+4\vdots 6$

$\Rightarrow a+b+4=6m$ với $m$ nguyên dương

$\Rightarrow a+b=6m-4$

Mặt khác:
$4^a\equiv 1^a\equiv 1\pmod 3$. Mà $4^a\vdots 2$ với mọi số nguyên dương $a$ nên $4^a$ có dạng $6k+4$ với $k$ nguyên dương

Do đó:

$4^a+a+b=6k+4+6m-4=6(k+m)\vdots 6$ (đpcm)

Lời giải:

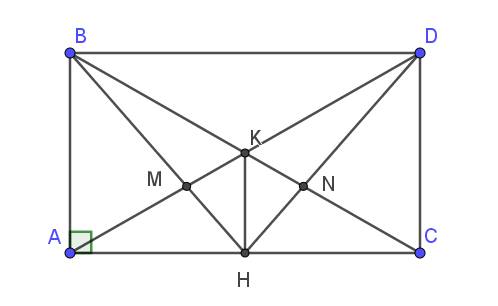
a/ Xét tam giác $BKA$ và $CKD$ có:
$BK=CK$ (do $K$ là trung điểm $BC$)
$KA=KD$ 

$\widehat{BKA}=\widehat{CKD}$ (đối đỉnh)

$\Rightarrow \triangle BKA=\triangle CKD$ (c.g.c)

$\Rightarrow \widehat{BAK}=\widehat{CDK}$. Mà hai góc này ở vị trí so le trong nên $CD\parallel AB$

b.

Từ $CD\parallel AB, AB\perp AC$ nên $CD\perp AC$

$\Rightarrow \widehat{DCH}=90^0$

Từ $\triangle BKA=\triangle CKD\Rightarrow AB=CD$

Xét tam giác $BAH$ và $DCH$ có:

$AH=CH$ 
$AB=CD$

$\widehat{BAH}=\widehat{DCH}=90^0$

$\Rightarrow \triangle BAH=\triangle DCH$ (c.g.c)

$\Rightarrow \widehat{H_1}=\widehat{H_2}$
Xét tam giác $BAC$ và $DCA$ có:

$AB=CD$

$\widehat{BAC}=\widehat{DCA}=90^0$

$AC$ chung

$\Rightarrow \triangle BAC=\triangle DCA$ (c.g.c)

$\Rightarrow \widehat{A_1}=\widehat{C_1}$
Xét tam giác $AMH$ và $CNH$ có:

$\widehat{A_1}=\widehat{C_1}$
$\widehat{H_1}=\widehat{H_2}$

$AH=CH$ 

$\Rightarrow \triangle AMH=\triangle CNH$ (g.c.g)

$\Rightarrow MH=NH$

$\Rightarrow MNH$ cân tại $H$

c.

Từ $\triangle BAC=\triangle DCA\Rightarrow BC=DA\Rightarrow BC:2=DA:2\Rightarrow CK=AK$

Xét tam giác $KHA$ và $KHC$ có:

$KH$ chung

$AK=CK$

$AH=CH$

$\Rightarrow \triangle KHA=\triangle KHC$ (c.c.c)

$\Rightarrow \widehat{AKH}=\widehat{CKH}$

$\Rightarrow KH$ là phân giác $\widehat{AKC}$

Hình vẽ:

a: \(BE+CE=BC\)

=>\(CE+\dfrac{1}{3}BC=BC\)

=>\(EC=\dfrac{2}{3}BC\)

Ta có: BD=BA

mà B nằm giữa D và A

nên B là trung điểm của DA

Xét ΔCAD có

CB là đường trung tuyến

\(CE=\dfrac{2}{3}CB\)

Do đó: E là trọng tâm của ΔCAD

Xét ΔCAD có

E là trọng tâm

AE cắt CD tại K

Do đó: K là trung điểm của CD

=>KC=KD

b: Xét ΔDAC có

E là trọng tâm

DE cắt AC tại M

Do đó: M là trung điểm của AC

=>\(DE=\dfrac{2}{3}DM=\dfrac{2}{3}\cdot9=6\left(cm\right)\)

Ta có DE+EM=DM

=>EM+6=9

=>EM=3(cm)

Ta có:

54 = 9.6.1 = 3.3.2

Các số có thể lập được là:

169; 196; 619; 691; 916; 961;

233; 323; 332

Vậy có 9 số có ba chữ số mà tích các chữ số là 54

54 = 9.6.1 = 3.3.2

Các số có thể lập được là:

169; 196; 619; 691; 916; 961;

233; 323; 332

Vậy có 9 số có ba chữ số mà tích các chữ số là 54

`c-(x^2+2x+1)=x^3+3x^2 -2x^2+7`

`=> c-x^2-2x-1=x^3+3x^2 -2x^2+7`

`=> c=x^3+3x^2 -2x^2+7+x^2+2x+1`

`=c=x^3 + (3x^2 -2x^2+x^2) + 2x+(7+1)`

`=>c=x^3 + 2x^2 +2x+8`

Sao lại có dấu "=" ở dòng 4 

\(\left(x-1\right)+B=A\)
\(\Rightarrow B=A-\left(x-1\right)\)

\(\Rightarrow B=\left(x^3+3x^2-2x^2+7\right)-\left(x-1\right)\)

\(\Rightarrow B=\left(x^3+x^2+7\right)-\left(x-1\right)\)

\(\Rightarrow B=x^3+x^2+7-x+1\)

\(\Rightarrow B=x^3+x^2-x+8\)