x2(1+2x)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(VT=\left(x-2y\right)^2-2x\left(4x+5y\right)\)
\(=\left(x^2-2\cdot x\cdot2y+4y^2\right)-\left(8x^2+10xy\right)\)
\(=x^2-4xy+4y^2-8x^2-10xy\)
\(=4y^2-7x^2-14xy\)
Ta thấy \(VT\ne VP\) nên đẳng thức không đúng

(3x-5)(2x+1)-(2x-1)^2-2x(x-2)-x+10=4
=>6x^2+3x-10x-5-(4x^2-4x+1)-2x^2+4x-x+10=4
=>(6x^2-4x^2-2x^2)+(3x-10x+4x+4x-x)+(-5-1+10)=4
=>4=4

`A= x^2+2xy-3x^2 +2y^2+3x^2-y^2`
`= (x^2-3x^2 +3x^2) +2xy +(2y^2 -y^2)`
`= x^2 +2xy +y^2`
`=(x+y)^2`
A = \(x^2\) + 2\(xy\) - 3\(x^2\) + 2y2 + 3\(x^2\) - y2
A = (\(x^2\)- 3\(x^2\) + 3\(x^2\)) + 2\(xy\) + (2\(y^2\) - y2)
A = \(x^2\) + 2\(xy\) + y2
A = (\(x\) + y)2

Lời giải:
PT $\Leftrightarrow 8x^3-16x^2+6x+2=0$
$\Leftrightarrow (8x^3-8x^2)-(8x^2-8x)-(2x-2)=0$
$\Leftrightarrow 8x^2(x-1)-8x(x-1)-2(x-1)=0$
$\Leftrightarrow (x-1)(8x^2-8x-2)=0$
$\Leftrightarrow 2(x-1)(4x^2-4x-1)=0$
$\Leftrightarrow x-1=0$ hoặc $4x^2-4x-1=0$
Nếu $x-1=0\Leftrightarrow x=1$
Nếu $4x^2-4x-1=0$
$\Leftrightarrow (2x-1)^2-2=0$
$\Leftrightarrow (2x-1-\sqrt{2})(2x-1+\sqrt{2})=0$
$\Leftrightarrow x=\frac{1\pm \sqrt{2}}{2}$

\((x+3y)^2\\=x^2+2\cdot x\cdot3y+(3y)^2\\=x^2+6xy+9y^2\\---\\(x-5xy)^2\\=x^2-2\cdot x\cdot5xy+(5xy)^2\\=x^2-10x^2y+25x^2y^2\)
\((5+9y)^3\\=5^3+3\cdot5^2\cdot9y+3\cdot5\cdot(9y)^2+(9y)^3\\=125+675y+1215y^2+729y^3\\---\\(6x-7xy)^3\\=(6x)^3-3\cdot(6x)^2\cdot7xy+3\cdot6x\cdot(7xy)^2-(7xy)^3\\=216x^3-756x^3y+882x^3y^2-343x^3y^3\)

\(4\left(x+3\right)\left(x^2-3x+9\right)-x\left(4x^2-3x\right)=6x+108\)
\(\Leftrightarrow4\left(x^3+27\right)-\left(4x^3-3x^2\right)=6x+108\)
\(\Leftrightarrow4x^3+108-4x^3+3x^2=6x+108\)
\(\Leftrightarrow3x^2+108=6x+108\)
\(\Leftrightarrow3x^2-6x=108-108\)
\(\Leftrightarrow3x\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=0\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

Do ABCD là hình thang cân (AB//CD) nên:
\(\widehat{A}+\widehat{D}=180^o\)
Mà: \(\widehat{C}=\widehat{D}\)
\(\Rightarrow\widehat{A}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{A}=\left(180^o+20^o\right):2=100^o\)
\(\Rightarrow\widehat{C}=180^o-100^o=80^o\)
Vậy số đo của góc \(\widehat{A}\) và \(\widehat{C}\) lần lượt là: \(100^o\) và \(80^o\)
⇒ Chọn B
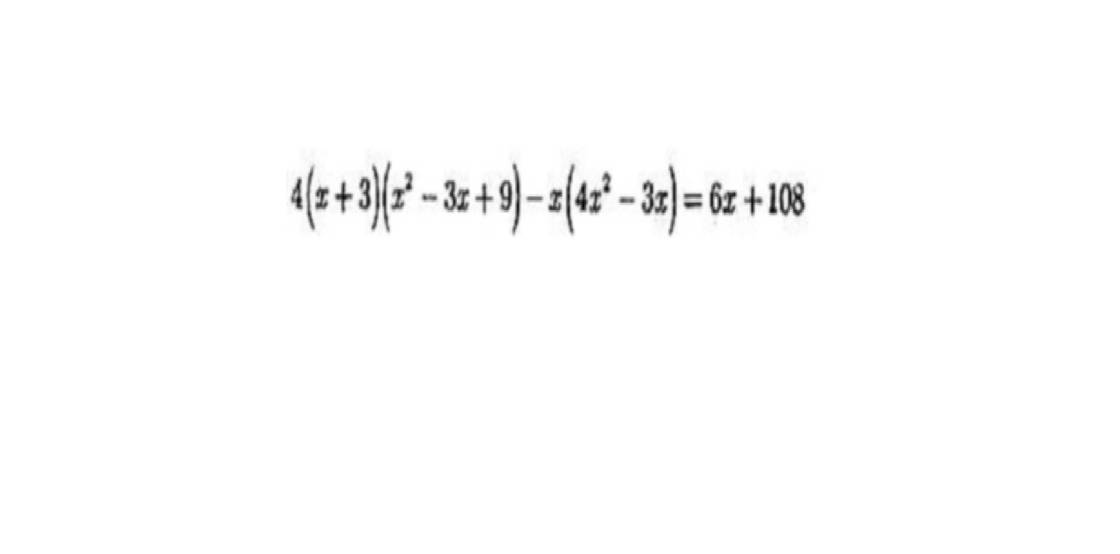

\(x^2\left(1+2x\right)\)
\(=x^2\cdot1+x^2\cdot2x\)
\(=x^2+2\cdot x^{1+2}\)
\(=x^2+2x^3\)