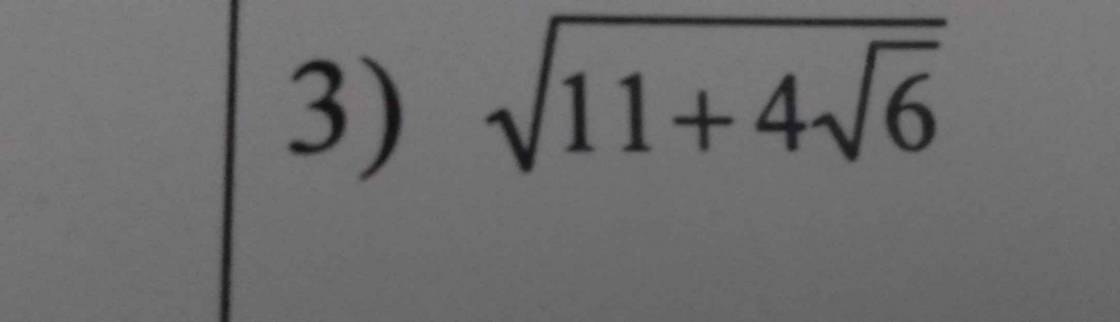\(\sqrt{11+4\sqrt{6}}\)

\(=\sqrt{8+4\sqrt{2.3}+3}\)

\(=\sqrt{\left(2\sqrt{2}\right)^2+2.2\sqrt{3}.\sqrt{2}+\left(\sqrt{3}\right)^2}\)

\(=\sqrt{\left(2\sqrt{2}+\sqrt{3}\right)^2}\)

\(=\left|2\sqrt{2}+\sqrt{3}\right|\)

\(=2\sqrt{2}+\sqrt{3}\)

A,B,C >0 ạ.

Chứng minh : `(a+b)^{3}+c^{3}-3ab(a+b+c)>0`

`<=>(a+b+c)[(a+b)^{2}-c(a+b)+c^{2}]-3ab(a+b+c)>0`

`<=>(a+b+c)(a^{2}+2ab+b^{2}-ac-bc+c^{2}-3ab)>0`

`<=>(a+b+c)(a^{2}+b^{2}+c^{2}-ac-bc-ab)>0`

`<=>(a+b+c)(2a^{2}+2b^{2}+2c^{2}-2ac-2bc-2ab)>0`

`<=>(a+b+c).[(a-b)^{2}+(b-c)^{2}+(c-a)^{2}]>0`

Ta thấy :

+) `a+b+c>0` ( do `a,b,c>0` ) 

+) `(a-b)^{2}+(b-c)^{2}+(c-a)^{2}>=0`

Dấu "=" xảy ra khi `a=b=c`

Mình nghĩ bạn thiếu đề là : 3 số abc đôi một khác nhau.

Vậy đã chứng minh được đề.

Em nên chèn bằng công thức nhé, chứ em viết thế này cô không hiểu đúng đề bài em cần được để trợ giúp em đâu

 Ta có \(3n^3-1011⋮1008\)

\(\Leftrightarrow\left(3n^3-3\right)-1008⋮1008\) 

\(\Leftrightarrow3\left(n^3-1\right)⋮1008\) 

\(\Leftrightarrow n^3-1⋮336\)\(⋮48\) 

\(\Rightarrow\left(n-1\right)\left(n^2+n+1\right)⋮48\).

Do \(n^2+n+1\) là số lẻ với mọi \(n\inℤ\) nên suy ra được \(n-1⋮48\), đpcm.

Giả sử n là số chẵn ta có: 3n³ là số chẵn ⇒ 3n³ - 1011 là số lẻ 

⇒ 3n³ - 1011 không chia hết cho 1008 vậy điều giả sử là sai 

⇒ n là số lẻ. Mặt khác ta cũng có:

3n³ - 1011 ⋮ 1008 ⇔ 3n³ - 3 -1008 ⋮ 1008 ⇔ 3n³ - 3 ⋮ 1008

⇔3(n³-1)⋮ 1008⇔ n³ - 1⋮ 336 ⇔ n³ - 1⋮ 48 ⇔(n-1)(n²+n+1)⋮48(1)

vì n là số lẻ (chứng minh trên) nên ta có: n² + n + 1 là số lẻ 

⇔ n² + n + 1 không chia hết cho 48 (2)

Kết hợp(1) và (2) ta có: n - 1 ⋮ 48 (đpcm)

Với \(p=2\) thì \(2p^4-p^2+16=44\) không là số chính phương. 

Với \(p=3\) thì \(2p^4-p^2+16=169\) là số chính phương.

Với \(p\ge5\), suy ra \(p⋮̸3\). Dễ dàng kiểm chứng \(p^2\equiv1\left(mod3\right)\) còn \(2p^4\equiv2\left(mod3\right)\). Lại có \(16\equiv1\left(mod3\right)\) nên \(2p^4-p^2+16\equiv2\left(mod3\right)\), do đó \(2p^4-p^2+16\) không thể là số chính phương.

 Như vậy, số nguyên tố \(p\) duy nhất thỏa mãn ycbt là \(p=3\)

Mình quên mất là không cần xét \(p=2\) đâu vì đề bài cho \(p\) nguyên tố lẻ.

A B x C y D E F M

a/

D và E cùng nhìn MC dưới 1 góc vuông -> CDME là tứ giác nội tiếp

b/

CM tương tự ta cũng có tứ giác BDMF là tứ giác nội tiếp

\(\Rightarrow\widehat{MBF}=\widehat{MDF}\) (góc nt cùng chắn cung MF) (1)

Xét tứ giác nt CDME có

\(\widehat{MCE}=\widehat{MDE}\) (góc nt cùng chắn cung MF) (2)

Từ (1) và (2) \(\Rightarrow\widehat{MBF}+\widehat{MCE}=\widehat{MDF}+\widehat{MDE}=\widehat{EDF}\) (3)

Xét \(\Delta ABC\) có

AB=AC (Hai tiếp tuyến cùng xp từ 1 điểm)

=> \(\Delta ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}=\dfrac{180^o-\widehat{xAy}}{2}=\dfrac{180^o-60^o}{2}=60^o\)

Ta có

\(sđ\widehat{ABC}=\dfrac{1}{2}sđ\) cung BC => sđ cung BC = 2.sđ \(\widehat{ABC}=2.60^o=120^o\) 

=> sđ cung BM + sđ cung CM = sđ cung BC \(=120^o\)

Ta có

\(sđ\widehat{MBF}=\dfrac{1}{2}sđ\)  cung BM (góc giữa tiếp tuyến và dây cung)

\(sđ\widehat{MCE}=\dfrac{1}{2}sđ\) cung CM (góc giữa tiếp tuyến và dây cung)

\(\Rightarrow sđ\widehat{MBF}+sđ\widehat{MCE}=sđ\widehat{EDF}=\dfrac{sđcungBM+sđcungCM}{2}=\dfrac{sđcungBC}{2}=\dfrac{120^0}{2}=60^o\)

c/

Xét tg vuông MBF và tg vuông MCD có

\(sđ\widehat{MBF}=\dfrac{1}{2}sđcungBM\) (góc giữa tiếp tuyến và dây cung)

\(sđ\widehat{MCD}=\dfrac{1}{2}sđcungBM\) (góc nt)

\(\Rightarrow\widehat{MBF}=\widehat{MCD}\) => tg MBF đồng dạng với tg MCD

\(\Rightarrow\dfrac{MF}{MD}=\dfrac{MB}{MC}\)

CM tương tự ta cũng có tg vuông MCE đồng dạng với tg vuông MBD

\(\Rightarrow\dfrac{ME}{MD}=\dfrac{MC}{MB}\Rightarrow\dfrac{MD}{ME}=\dfrac{MB}{MC}\)

\(\Rightarrow\dfrac{MF}{MD}=\dfrac{MD}{ME}\Rightarrow MD^2=ME.MF\left(đpcm\right)\)

Giả sử \(y\) là số lẻ

Đặt \(\left\{{}\begin{matrix}x^2-y=m^2\\x^2+y=n^2\end{matrix}\right.\left(m,n\inℕ;m< n\right)\)

\(\Rightarrow2y=n^2-m^2\) \(\Rightarrow n^2-m^2\) chia hết cho 2 nhưng không chia hết cho 4.

 Thế nhưng, ta thấy \(n^2\) và \(m^2\) khi chia cho 4 chỉ có thể có số dư là 0 hoặc 1, vậy nên \(n^2-m^2\) khi chia cho 4 sẽ chỉ có số dư là \(0,1,-1\), nghĩa là nếu \(n^2-m^2\) mà chia hết cho 2 thì buộc hiệu này phải chia hết cho 4, mâu thuẫn. Vậy điều giả sử là sai \(\Rightarrow\) đpcm.