
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



bài toán rất hay cảm ơn bạn đã chia sẻ cho mọi người tham khảo
xét dãy số 1; 2; 3; 4; .....; 2018
khoảng cách của dãy số là 2 -1 = 1
dãy số trên có số số hạng ( 2018 - 1 ) : 1 + 1 = 2018 (số)
cứ 1 lần xóa số số hạng bớt đi 1 số
vậy để trên bảng còn lại duy nhất 1 số thì số lần xóa là
(2018 - 1 ) = 2017 (lần xóa)
vì cứ mỗi lần xóa lại thêm vào một số bằng tổng của hai số bị xóa trên bảng, nên cứ sau mỗi lần xóa thì mất đi 1 số nhưng tổng của các số trên bảng không đổi so với ban đầu
vậy sau 2017 lần xóa thì trên bảng còn lại 1 số duy nhất bằng tổng tất cả các số trên bảng lúc đầu khi chưa xóa
tổng tất cả các số trên bảng là :
1 + 2 + 3 + 4 + .....+ 2018
= ( 2018 + 1) x 2018 : 2 = 2037171
vậy sau 2017 lần xóa trên bảng còn lại duy nhất 1 số là số lẻ

279 =( 33)9 = 327=326.3 < 326 . 213 = (32)13. 213 = 913.213 = 1813
vậy 279 < 1813

giả sử thêm 2 học sinh vào khối 6 thì số học sinh khối 6 lúc sau xếp mỗi hàng 3 em , 4 em hay 5 em đều vừa đủ hay số học sinh khối 6 lúc sau thuộc bội chung của 3; 4; 5
BCNN(3; 4; 5) = 3 x 4 x 5 = 60
số học sinh khối 6 lúc sau \(\in\) B(60)
mà B(60) = {0; 60; 120; 180; .....}
vì 150 < số học sinh khối 6 < 200
⇒ số học sinh khối lúc sau là 180
số học sinh khối 6 là 180 - 2 = 178 (học sinh)
đs.... (thử lại kết quả biết đúng sai ta có 150 < 178 < 200 (đúng)
178 : 3; 4; 5 đều có số dư lần lượt là 1; 2; 3 (đúng)

câu này có trong đề kiểm tra kỳ 1 của trường thcs amsterdam Hà Nội năm 2019 - 2020
A = \(\dfrac{\dfrac{1}{2017}+\dfrac{2}{2016}+\dfrac{3}{2015}+......+\dfrac{2017}{1}}{\dfrac{1}{2}+\dfrac{1}{3}+......+\dfrac{1}{2018}}\)
Đặt tử số của A là B = \(\dfrac{1}{2017}\) + \(\dfrac{2}{2016}\)+....\(\dfrac{2017}{1}\)
B =1+ ( \(\dfrac{1}{2017}\)+1) + ( \(\dfrac{2}{2016}\)+1) + ( \(\dfrac{3}{2015}\)+ 1)+ ...+(\(\dfrac{2016}{2}\)+1)
B = 1 + \(\dfrac{2018}{2017}\)+ \(\dfrac{2018}{2016}\)+\(\dfrac{2018}{2015}\)+.....+\(\dfrac{2018}{4}\)+\(\dfrac{2018}{3}\)+ \(\dfrac{2018}{2}\)
B =2018 . ( \(\dfrac{1}{2018}\)+ \(\dfrac{1}{2017}\)+ \(\dfrac{1}{2016}\)+......+\(\dfrac{1}{4}\)+\(\dfrac{1}{3}\)+\(\dfrac{1}{2}\))
vậy A = 2018 x \(\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+.....+\dfrac{1}{2016}+\dfrac{1}{2017}+\dfrac{1}{2018}}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+.......+\dfrac{1}{2016}+\dfrac{1}{2017}+\dfrac{1}{2018}}\)
A = 2018 = B
kết luận A = B


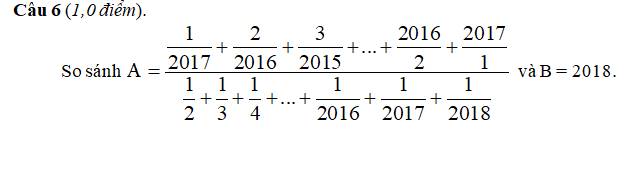

Câu 3:
a. Vì $\overline{2a3b}\vdots 90$ nên nó cũng chia hết cho $10$
Do đó $b=0$
$\overline{2a30}\vdots 90$ nên nó cũng chia hết cho $9$
$\Rightarrow 2+a+3+0\vdots 9$
Hay $5+a\vdots 9$
Vì $a$ là số tự nhiên có 1 chữ số nên $a=4$
Vậy số cần tìm là $2430$
b.
Một số chính phương sẽ có dạng $a^2$ với $a$ là 1 số tự nhiên
Nếu $a$ chẵn, $a\vdots 2$ nên $a^2=a.a$ chia hết cho $4$, hay $a^2$ chia $4$ dư $0$
Nếu $a$ lẻ. Đặt $a=2k+1$ với $k$ tự nhiên. Khi đó:
$a^2=(2k+1)^2=4k^2+4k+1=4(k^2+k)+1$ chia $4$ dư $1$
Vậy $a^2$ chia $4$ có dư $0$ hoặc $1$