Giúp Tớ Có 1 Cái Tết Thảnh Thơi Đi Mọi Người :Đ![]()
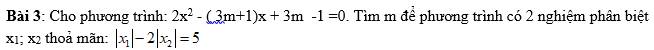
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

d,
Ta liệt kê các ước của số 70: 1, 2, 5, 7, 10, 14, 35, 70.
Ta xem xét từng số trong danh sách ước trên để tìm số nguyên x thỏa mãn yêu cầu.
- Khi x = 1, không chia hết cho 7.
- Khi x = 2, không chia hết cho 7.
- Khi x = 5, không chia hết cho 7.
- Khi x = 7, chia hết cho 7 và là ước của 70. Vậy x = 7 là một giá trị thỏa mãn yêu cầu.
Vậy, số nguyên x thỏa mãn yêu cầu là x = 7.
e,
Ta có thể thử từng giá trị của x để xem xét xem 2x - 1 có chia hết cho 30 hay không.
- Khi x = 1, ta có 2x - 1 = 2(1) - 1 = 1. 1 không chia hết cho 30.
- Khi x = 2, ta có 2x - 1 = 2(2) - 1 = 3. 3 không chia hết cho 30.
- Khi x = 3, ta có 2x - 1 = 2(3) - 1 = 5. 5 không chia hết cho 30.
- Khi x = 4, ta có 2x - 1 = 2(4) - 1 = 7. 7 không chia hết cho 30.
- Khi x = 5, ta có 2x - 1 = 2(5) - 1 = 9. 9 không chia hết cho 30.
- Khi x = 6, ta có 2x - 1 = 2(6) - 1 = 11. 11 không chia hết cho 30.
- Khi x = 7, ta có 2x - 1 = 2(7) - 1 = 13. 13 không chia hết cho 30.
- Khi x = 8, ta có 2x - 1 = 2(8) - 1 = 15. 15 không chia hết cho 30.
- Khi x = 9, ta có 2x - 1 = 2(9) - 1 = 17. 17 không chia hết cho 30.
- Khi x = 10, ta có 2x - 1 = 2(10) - 1 = 19. 19 không chia hết cho 30.
Từ các kết quả trên, ta thấy không có giá trị nào của x mà 2x - 1 là ước của 30. Vậy không có số nguyên x thỏa mãn điều kiện đề bài.
f,
Ta có thể thử từng giá trị của x và kiểm tra xem f(x+2) có phải là ước của 2x-1 :
Nếu x = 1:
f(1+2) = f(3)
2(1)-1 = 1
f(3) = 1
Ta thấy f(3) = 1 không phải là ước của 2(1)-1 = 1.
Nếu x = 2:
f(2+2) = f(4)
2(2)-1 = 3
f(4) = 3
Ta thấy f(4) = 3 không phải là ước của 2(2)-1 = 3.
Nếu x = 3:
f(3+2) = f(5)
2(3)-1 = 5
f(5) = 5
Ta thấy f(5) = 5 là ước của 2(3)-1 = 5.
Vậy, số nguyên x = 3 làm cho f(x+2) là ước của 2x-1.
Tham khỏa thôi nha.

a)
Số học sinh lớp 6a là:
\(26:\dfrac{13}{20}=40\left(hs\right)\)
b)
Số học sinh đạt là:
\(40\cdot\dfrac{1}{8}=5\left(hs\right)\)
Số học sinh ở mức khá là:
\(40-26-5=9\left(hs\right)\)
Đáp số: a) 40 học sinh
b) 9 học sinh và 5 học sinh

Mẫu số chung 2 phân số: 2929
\(\dfrac{18}{29}=\dfrac{18\cdot101}{29\cdot101}=\dfrac{1818}{2929}\)
\(\dfrac{70}{101}=\dfrac{70\cdot29}{101\cdot29}=\dfrac{2030}{2929}\)
Vì \(1818< 2030\) nên\(\dfrac{1818}{2929}< \dfrac{2030}{2929}\)
Vậy \(\dfrac{18}{29}< \dfrac{70}{101}\)

Lời giải:
Do $a-b=13$ nên:
\(\frac{3a-b}{2a+13}-\frac{3b-a}{2b-13}=\frac{3a-(a-13)}{2a+13}-\frac{3b-(13+b)}{2b-13}\)
\(=\frac{2a+13}{2a+13}-\frac{2b-13}{2b-13}=1-1=0\)

Vì \(p\) là số nguyên tố lớn hơn 3 nên \(p\) có dạng \(3k+1\) hoặc \(3k+2\)
TH1: Nếu \(p=3k+1\) thì vì p là SNT nên \(k\) chẵn \(\Rightarrow k=2n\) \(\Rightarrow p=6n+1\)
\(\Rightarrow\)\(P=\left(p-1\right)\left(p+1\right)\)
\(=6n\left(6n+2\right)\)
\(=12n\left(3n+1\right)\)
Nếu \(n\) chẵn thì \(n\left(3n+1\right)⋮2\) \(\Rightarrow P=12n\left(3n+1\right)⋮12.2=24\)
Nếu \(n\) lẻ thì \(3n+1⋮2\) \(\Rightarrow P=12n\left(3n+1\right)⋮12.2=24\)
Vậy \(P⋮24\), đpcm.
TH \(p=3k+2\) thì suy ra \(k\) lẻ \(\Rightarrow k=2n+1\) rồi xét tương tự nhé

\(\dfrac{1}{6}\) = \(\dfrac{1.20}{6.20}=\dfrac{20}{120}\)
\(\dfrac{5}{8}=\dfrac{5.15}{8.15}=\dfrac{75}{120}\)
\(\dfrac{4}{5}=\dfrac{4.24}{5.24}=\dfrac{96}{120}\)
Vậy các phân số:\(\dfrac{1}{6};\dfrac{5}{8};\dfrac{4}{5}\)đã được quy đồng mẫu số thành các phân số: \(\dfrac{20}{120};\dfrac{75}{120};\dfrac{96}{120}\)

Cách tính số hạng thứ n trong dãy số là (số cuối-số đầu):(khoảng cách)+1
VD.tính số hạng từ 1;2;3;...;100
Cách tính (100-1):1+1=100( số)
VD.tính số hạng từ 0;2;4;...; 100
Cách tính (100-0):2+1=51 (số)

Đổi: \(40\%=\dfrac{2}{5}\)
Tổng số phần bằng nhau là:
\(2+5=7\) (phần)
Số vải may áo là:
\(345:7\times5=\dfrac{1725}{7}\left(m\right)\)
Đáp số: ...

\(m\times25+m\times176-m\)
\(=m\times\left(25+176-1\right)\)
\(=m\times\left(25+175\right)\)
\(=m\times200\)
Lời giải:
Để pt có 2 nghiệm phân biệt thì:
$\Delta'=(3m+1)^2-8(3m-1)>0$
$\Leftrightarrow 9(m^2-2m+1)>0$
$\Leftrightarrow 9(m-1)^2>0$
$\Leftrightarrow m-1\neq 0\Leftrightarrow m\neq 1$
Áp dụng định lý Viet, với $x_1,x_2$ là nghiệm của pt thì:
$x_1+x_2=\frac{3m+1}{2}$
$x_1x_2=\frac{3m-1}{2}$
$\Rightarrow x_1x_2+1-(x_1+x_2)=0$
$\Leftrightarrow (x_1-1)(x_2-1)=0$
$\Leftrightarrow x_1=1$ hoặc $x_2=1$
Vì $|x_1|=2|x_2|+5\geq 5$ nên $x_2=1$
Khi đó:
$|x_1|=2|x_2|+5=2.1+5=7$
$\Rightarrow x_1=\pm 7$
Nếu $x_1=7$:
$\Rightarrow x_1+x_2=\frac{3m+1}{2}$
$\Leftrightarrow 8=\frac{3m+1}{2}\Leftrightarrow m=5$ (tm)
Nếu $x_1=-7$:
$\Rightarrow x_1+x_2=\frac{3m+1}{2}$
$\Leftrightarrow -6=\frac{3m+1}{2}$
$\Leftrightarrow m=\frac{-13}{3}$