Đây là toán lớp 5 à bạn 

chữ số tận cùng là chữ số 8

Nếu k là số lẻ thì 15k + 1 là số chẵn hay 15k + 1 là hợp số.

Nếu k là số chẵn thì 15k + 1 có thể là hợp số cũng có thể là số nguyên tố.

Với mọi k \(\in\) N thì 15k + 1 là hợp số hay nguyên tố chưa thể xác định được.

phần a sai đề bạn nhé

Lời giải:

a. Chiều rộng bể cá: $1,2\times \frac{2}{3}=0,8$ (m) 

Chiều cao bể cá: $0,8\times \frac{2}{3}=\frac{8}{15}$ (m) 

Thể tích bể: 

$1,2\times 0,8\times \frac{8}{15}=0,512$ (m³) 

b. 

Nếu 15% bể không chứa nước thì bể chứa số lít nước là:

0,512\times (100-15)\times 100=0,4352$ (m³) = 435,2 lít

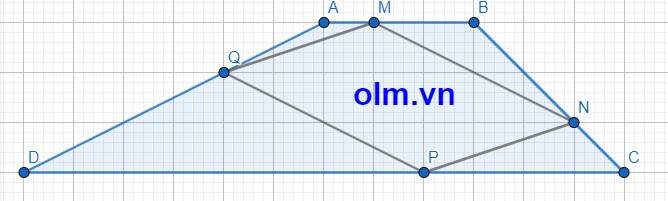
      \(\dfrac{AM}{AB}\) = \(\dfrac{1}{1+2}\) = \(\dfrac{1}{3}\) 

S_AMQ  = \(\dfrac{1}{3}\) S_ABQ  (vì hai tam giác có chung chiều cao hạ từ đỉnh Q xuống đáy AB và AM = \(\dfrac{1}{3}\)AB)

   \(\dfrac{AQ}{AD}\) = \(\dfrac{1}{1+2}\) = \(\dfrac{1}{3}\) 

S_ABQ = \(\dfrac{1}{3}\)S_ABD (Vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AD và AQ = \(\dfrac{1}{3}\)AD)

S_AQM = \(\dfrac{1}{3}\)\(\times\)\(\dfrac{1}{3}\)S_ABD = \(\dfrac{1}{9}\)S_ABD

    \(\dfrac{BN}{BC}\) = \(\dfrac{2}{2+1}\) = \(\dfrac{2}{3}\)

    \(\dfrac{BM}{AB}\) = \(\dfrac{2}{2+1}\) = \(\dfrac{2}{3}\)

    Chứng minh tương tự ta có:

S_BMN =  \(\dfrac{2}{3}\)\(\times\)\(\dfrac{2}{3}\)S_ABC  = \(\dfrac{4}{9}\)S_ABC 

 \(\dfrac{CN}{CB}\) = \(\dfrac{1}{2+1}\) = \(\dfrac{1}{3}\)

  \(\dfrac{CP}{CD}\) = \(\dfrac{1}{2+1}\) = \(\dfrac{1}{3}\) 

 Chứng minh tương tự ta có:

   S_CPN = \(\dfrac{1}{3}\) \(\times\) \(\dfrac{1}{3}\)S_BCD = \(\dfrac{1}{9}\)S_BCD

   \(\dfrac{DQ}{AD}\) = \(\dfrac{2}{2+1}\) = \(\dfrac{2}{3}\)

  \(\dfrac{DP}{DC}\) = \(\dfrac{2}{2+1}\)  = \(\dfrac{2}{3}\)

Chứng minh tương tự ta có:

   S_DPQ = \(\dfrac{2}{3}\) \(\times\) \(\dfrac{2}{3}\)S_ABD = \(\dfrac{4}{9}\)S_ADC

S_AMQ + S_BMN + S_CNB + S_DPQ = \(\dfrac{1}{9}\)S_ABD+\(\dfrac{4}{9}\)S_ABC+\(\dfrac{1}{9}\)S_BCD+\(\dfrac{4}{9}\)S_ADC = \(\dfrac{5}{9}\)S_ABCD

S_MNPQ = S_ABCD - \(\dfrac{5}{9}\)S_ABCD = \(\dfrac{4}{9}\)S_ABCD = 360 x \(\dfrac{4}{9}\) = 160 (cm²)

Đs:... 

\(\dfrac{20}{35}=\dfrac{20:5}{35:5}=\dfrac{4}{7}\\ \dfrac{33}{121}=\dfrac{33:11}{121:11}=\dfrac{3}{11}\)

Lời giải:

$\frac{20}{35}=\frac{20:5}{35:5}=\frac{4}{7}$

$\frac{33}{121}=\frac{33:11}{121:11}=\frac{3}{11}$

Bổ sung đề. ∆ABC cân tại A

a) Do ∆ABC cân tại A (gt)

⇒ ∠C = ∠B = 70⁰

Ta có:

∠A + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)

⇒ ∠A = 180⁰ - (∠B + ∠C)

= 180⁰ - (70⁰ + 70⁰)

= 40⁰

b) Do ∆ABC cân tại A (gt)

⇒ ∠B = ∠C = 50⁰

Ta có:

∠A + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)

⇒ ∠A = 180⁰ - (∠B + ∠C)

= 180⁰ - (50⁰ + 50⁰)

= 80⁰

c) Do ∆ABC cân tại A (gt)

⇒ ∠B = ∠C

Ta có:

∠A + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)

⇒ ∠B + ∠C = 180⁰ - ∠A

= 180⁰ - 80⁰

= 100⁰

Mà ∠B = ∠C (cmt)

⇒ ∠B = ∠C = 100⁰ : 2 = 50⁰

Xét \(\Delta ABD\) và \(\Delta ACE\) có:

\(AB=AC\) (vì là hai cạnh bên trong tam giác cân)

\(\widehat{ABD}=\widehat{ACE}\) (vì là hai góc ở đáy trong tam giác cân)

\(BD=CE\left(gt\right)\)

\(\Rightarrow\Delta ABD=\Delta ACE\left(c.g.c\right)\)

\(\Rightarrow AD=AE\) (2 cạnh tương ứng)

Hay ΔADE cân tại A 

Do ∆ABC cân tại A (gt)

⇒ AB = AC và ∠B₁ = ∠C₁

Xét ∆ABD và ∆ACE có:

AB = AC (cmt)

∠B₁ = ∠C₁ (cmt)

BD = CE (gt)

⇒ ∆ABD = ∆ACE (c-g-c)

⇒ AD = AE (hai cạnh tương ứng)

⇒ ∆ADE cân tại A

trả lời nhanh cho mình

\(\dfrac{3}{5}\)  = \(\dfrac{3\times2}{5\times2}\) = \(\dfrac{6}{10}\) 

\(\dfrac{2}{7}\) = \(\dfrac{2\times3}{7\times3}\) =  \(\dfrac{6}{21}\)

Vậy 5 phân số  bé hơn \(\dfrac{3}{5}\) và lớn hơn \(\dfrac{2}{7}\) là hai phân số nằm giữa hai phân số \(\dfrac{6}{10}\) và \(\dfrac{6}{21}\) đó lần lượt là các phân số:

\(\dfrac{6}{20}\); \(\dfrac{6}{19}\); \(\dfrac{6}{18}\); \(\dfrac{6}{17}\); \(\dfrac{6}{16}\)

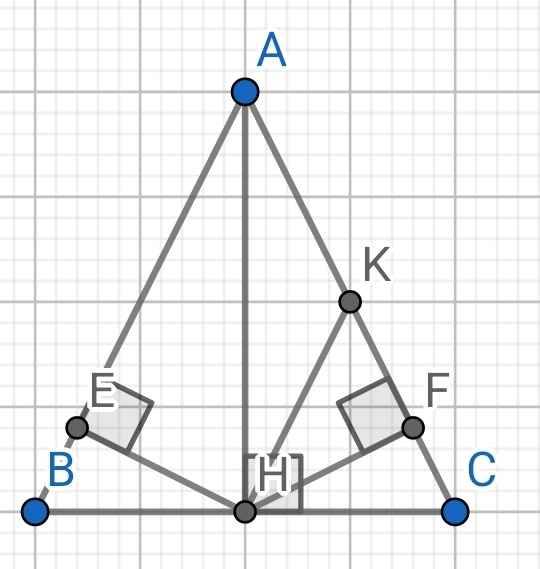
a) Do ∆ABC cân tại A (gt)

⇒ ∠ABC = ∠ACB và AB = AC

Do ∠ABC = ∠ACB (cmt)

⇒ ∠ABH = ∠ACH

Xét hai tam giác vuông: ∆ABH và ∆ACH có:

AB = AC (cmt)

∠ABH = ∠ACH (cmt)

⇒ ∆ABH = ∆ACH (cạnh huyền - góc nhọn)

b) Do ∆ABH = ∆ACH (cmt)

⇒ BH = CH (hai cạnh tương ứng)

Do ∠ABH = ∠ACH (cmt)

⇒ ∠EBH = ∠FCH

Xét hai tam giác vuông: ∆EBH và ∆FCH có:

BH = CH (cmt)

∠EBH = ∠FCH (cmt)

⇒ ∆EBH = ∆FCH (cạnh huyền - góc nhọn)

⇒ EB = FC (hai cạnh tương ứng)

c) Do HK // AB (gt)

⇒ ∠KHC = ∠ABC (đồng vị)

Mà ∠ABC = ∠ACB (cmt)

⇒ ∠KHC = ∠ACB

⇒ ∠KHC = ∠KCH

⇒ ∆KCH cân tại K

⇒ KH = KC (1)

Do ∆ABH = ∆ACH (cmt)

⇒ ∠BAH = ∠CAH (hai góc tương ứng)

⇒ ∠BAH = ∠KAH

Do HK // AB (gt)

⇒ ∠KHA = ∠BAH (so le trong)

Mà ∠BAH = ∠KAH (cmt)

⇒ ∠KHA = ∠KAH

⇒ ∆KAH cân tại K

⇒ KA = KH (2)

Từ (1) và (2) ⇒ KA = KC

Hay K là trung điểm của AC