
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(A=\left\{6;7;8;9;10;11\right\}\)
\(A=\left\{x\inℕ|5< x< 12\right\}\)
\(B=\left\{2;3;4;5;6;7;8;9;10;11\right\}\)
\(B=\left\{x\inℕ|1< x< 12\right\}\)
b) Tập hợp C vừa thuộc A vừa thuộc B
\(C=\left\{6;7;8;9;10;11\right\}\)
a) �={6;7;8;9;10;11}A={6;7;8;9;10;11}
�={�∈N∣5<�<12}A={x∈N∣5<x<12}
�={2;3;4;5;6;7;8;9;10;11}B={2;3;4;5;6;7;8;9;10;11}
�={�∈N∣1<�<12}B={x∈N∣1<x<12}
b) Tập hợp C vừa thuộc A vừa thuộc B
�={6;7;8;9;10;11}C={6;7;8;9;10;11}

a) \(A=\left\{1;2;3;4;5\right\}\)
\(\Rightarrow A=\left\{x\inℕ|1\le x\le5\right\}\)
b) \(B=\left\{0;1;2;3;4\right\}\)
\(\Rightarrow B=\left\{x\inℕ|0\le x\le4\right\}\)
c) \(C=\left\{1;2;3;4\right\}\)
\(\Rightarrow C=\left\{x\inℕ|1\le x\le4\right\}\)
d) \(D=\left\{0;2;4;6;8\right\}\)
\(\Rightarrow D=\left\{x\inℕ|x=2k;0\le k\le4;k\inℕ\right\}\)
e) \(E=\left\{1;3;5;7;9;...49\right\}\)
\(\Rightarrow E=\left\{x\inℕ|x=2k+1;0\le k\le24;k\inℕ\right\}\)
f) \(F=\left\{11;22;33;44;...99\right\}\)
\(\Rightarrow F=\left\{x\inℕ|x=11k;1\le k\le9;k\inℕ\right\}\)

F = 7 + 11 + 15 + 19 +...+ 203
Dãy số trên là dãy số cách đều với khoảng cách là: 11 - 7 = 4
Số số hạng của dãy số trên là: (203 - 7): 4 + 1 = 50
Tổng F là: (203 + 7) x 50: 2 = 5250

a) Số phần tử:
\(\left(9-2\right):1+1=8\) (phần tử)
b) Số phần tử:
\(\left(20-2\right):2+1=10\) (phẩn tử)
c) Số phần tử:
\(\left(25-1\right):3+1=9\) (phần tử)
d) Số phần tử:
\(\left(104-2\right):2+1=52\) (phần tử)
e) Số phần tử:
\(\left(470-5\right):5+1=94\) (phần tử)
f) Số phần tử:
\(\left(500-10\right):10+1=50\) (phần tử)

e) \(2^x+2^{x+3}=144\)
\(=>2^x+2^x.2^3=144\)
\(=>2^x.\left(1+2^3\right)=144\)
\(=>2^x.9=144\)
\(=>2^x=144:9\)
\(=>2^x=16=2^4\)
\(=>x=4\)
__________
f) \(3^x+3^{x+1}=108\)
\(=>3^x+3^x.3=108\)
\(=>3^x.\left(1+3\right)=108\)
\(=>3^x.4=108\)
\(=>3^x=108:4\)
\(=>3^x=27=3^3\)
\(=>x=3\)
\(#Wendy.Dang\)

a) 4915 = 4914.49 = (492)7.49 = (2 401)7.49
Vì (2 401)7 có chữ số tận cùng là 1 nên (2 401)7.49 có chữ số tận cùng là 9.
Vậy chữ số tận cùng của số 4915 là 9.
b) Ta có: \(54^{10}=\left(54^2\right)^5=2916^5\)
Tích của 5 chữ số 6 có chữ số tận cùng là 6 nên \(2916^5\) có chữ số tận cùng là 6.
Vậy \(54^{10}\) có chữ số tận cùng là 6.
c) Ta có 1120 có chữ số tận cùng là 1;
11921 có chữ số tận cùng là 9;
2 00022 có chữ số tận cùng là 0.
Khi đó 1120 + 11921 + 2 00022 có chữ số tận cùng là chữ số tận cùng của tổng 1 + 9 + 0 =10.
Vậy 1120 + 11921 + 2 00022 có chữ số tận cùng là 0.

Ta có A = 5 + 52 + 53 + ... + 52021
5A = 52 + 53 + 54 + ... + 52022
5A - A = ( 52 + 53 + 54 + ... + 52022 ) - ( 5 + 52 + 53 + ... + 52021 )
4A = 52022 - 5
A = \(\dfrac{5^{2022}-5}{4}\)
Tìm chữ số tận cùng của kết quả mỗi phép tính sau:
a. 4915
b. 5410
c. 1120+11921+200022

A = 1 + 2 + 3 +...+ 50
Dãy số trên là dãy số cách đều với khoảng cách là:
2 - 1 = 1
Số số hạng của dãy số trên là:
(50 - 1): 1 + 1 = 50
Tổng A là:
A = (50 + 1)x 50 : 2 = 1275
Muốn tính tổng của một dãy số cách đều em cần có kiến thức sau:
1, Tìm khoảng cách của dãy số cách đều bằng cách lấy số hạng sau trừ số hạng liền kề trước nó
2, Tìm số số hạng bằng cách lấy số cuối trừ số đầu được bao nhiêu chia cho khoảng cách rồi cộng 1
3, Tổng dãy số cách đều bằng (số cuối + số đầu) nhân số số hạng rồi chia 2
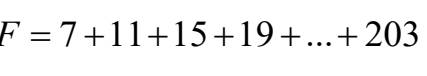
Các chữ số khác nhau mà có tổng bằng 5 là:
1 + 0 + 4= 5
2 + 0 + 3 = 5
Ta có các số thỏa mãn đề bài lần lượt là:
104; 140; 203; 230; 302; 320; 401; 410
Tập A có 8 phần tử