TÍNH HỢP LÝ:1.2.3.4.5.6.7.8.9-1.2.3.4.5.6.7.8-1.2.3.4.5.6.7-8^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(x=\dfrac{7}{25}+\dfrac{-1}{5}\)
\(\Rightarrow x=\dfrac{7}{25}+\dfrac{-5}{25}\)
\(\Rightarrow x=\dfrac{2}{25}\)c
b) \(x=\dfrac{5}{11}+\dfrac{4}{-9}\)
\(\Rightarrow x=\dfrac{45}{99}+\dfrac{-44}{99}\)
\(\Rightarrow x=\dfrac{1}{99}\)
c) \(x-\dfrac{5}{7}=\dfrac{1}{9}\)
\(\Rightarrow x=\dfrac{1}{9}+\dfrac{5}{7}\)
\(\Rightarrow x=\dfrac{7}{63}+\dfrac{45}{63}\)
\(\Rightarrow x=\dfrac{52}{63}\)
d) \(x-\dfrac{5}{7}=\dfrac{2}{7}\cdot\dfrac{11}{5}\)
\(\Rightarrow x-\dfrac{5}{7}=\dfrac{22}{35}\)
\(\Rightarrow x=\dfrac{22}{35}+\dfrac{5}{7}\)
\(\Rightarrow x=\dfrac{22}{35}+\dfrac{25}{35}\)
\(\Rightarrow x=\dfrac{47}{35}\)
e) \(\dfrac{3}{4}-x=1\)
\(\Rightarrow x=\dfrac{3}{4}-1\)
\(\Rightarrow x=-\dfrac{1}{4}\)
f) x + 4 = 1/5
x = 1/5 - 4
x = 1/5 - 20/5
x = -19/5
g) x - 1/5 = 2
x = 2 + 1/5
x = 10/5 + 1/5
x = 11/5
h) x + 5/3 = 1/27
x = 1/27 - 5/3
x = 1/27 - 45/27
x = -44/27
i) x/15 = 3/5 + (-2/3)
x/15 = 9/15 - 10/15
x/15 = -1/15
x = -1
k) 3x/4 = 18/(3x + 1)
3x(3x + 1) = 18.4 (1)
Đặt t = 3x
(1) ⇒ t(t + 1) = 72
t² + t - 72 = 0
t² - 8t + 9t - 72 = 0
(t² - 8t) + (9t - 72) = 0
t(t - 8) + 9(t - 8) = 0
(t - 8)(t + 9) = 0
t - 8 = 0 hoặc t + 9 = 0
*) t - 8 = 0
t = 8
3x = 8
x = 8/3
*) t + 9 = 0
t = -9
3x = -9
x = -9 : 3
x = -3
Vậy x = -3; x = 8/3

a; \(x\) = \(\dfrac{7}{25}\) + \(\dfrac{-1}{5}\)
\(x\) = \(\dfrac{7}{25}\) - \(\dfrac{5}{25}\)
\(x=\dfrac{2}{25}\)
b; \(x=\dfrac{5}{11}\) + \(\dfrac{4}{-9}\)
\(x=\dfrac{45}{99}-\dfrac{44}{99}\)
\(x=\dfrac{1}{99}\)
c; \(x\) - \(\dfrac{5}{7}\) = \(\dfrac{1}{9}\)
\(x\) = \(\dfrac{1}{9}\) + \(\dfrac{5}{7}\)
\(x=\dfrac{7}{63}+\dfrac{45}{63}\)
\(x\) = \(\dfrac{52}{63}\)

a; \(\dfrac{x}{7}\) = \(\dfrac{9}{y}\) (\(x>y\))
\(x.y\) = 7.9
\(xy\) = 63
Ư(63) = {-63;-21 -9; 7; -3; -1; 1; 3; 7; 9;21; 63}
Lập bảng ta có:
| \(x\) | -63 | -21 | -9 | -7 | -3 | -1 | 1 | 3 | 7 | 9 | 21 | 63 |
| y | -1 | -3 | -7 | -9 | -21 | -63 | 63 | 21 | 9 | 7 | 3 | 1 |
Vì \(x>y\) nên theo bảng trên ta có các cặp số nguyên \(x;y\) thỏa mãn đề bài là:
(\(x;y\)) = (-7; -9); (-3; -21); (-1; -63); (9; 7); (21; 3); (63; 1)
b; \(\dfrac{x}{15}\) = \(\dfrac{3}{y}\) Và \(x< y< 0\)
\(x.y\) = 3.15
\(xy\) = 45
45 = 32.5; Ư(45) = {-45; -15; -9; -5; -3; -1; 1; 3; 5; 9; 15; 45}
Lập bảng ta có:
| \(x\) | -45 | -15 | -9 | -5 | -3 | -1 | 1 | 3 | 5 | 9 | 15 | 45 |
| 4y | -1 | -3 | -5 | -9 | -15 | -45 | 45 | 15 | 9 | 5 | 3 | 1 |
Vì \(x< y< 0\)
Theo bảng trên ta có:
các cặp \(x;y\) nguyên thỏa mãn đề bài là:
(-45; -1); (-15; -3); (-9; -5)

Bài 3.17
a = \(\dfrac{n+8}{2n-5}\) (n \(\in\) N*)
a \(\in\) Z ⇔ n + 8 ⋮ 2n - 5
2.(n + 8) ⋮ 2n - 5
2n + 16 ⋮ 2n - 5
2n - 5 + 21 ⋮ 2n - 5
21 ⋮ 2n - 5
2n - 5 \(\in\) Ư(21)
21 = 3.7; Ư(21) = {-21; -7; -3; -1; 1; 3; 7; 21}
Lập bảng ta có:
| 2n - 5 | -21 | -7 | -3 | -1 | 1 | 3 | 7 | 21 |
| n | -8 (loại) | -1(loại) | -1(loại) | -2(loại) | 3 | 4 | 6 | 13 |
| a =\(\dfrac{n+8}{2n-5}\) | 11(loại) | 4(loại) | 2 | 1(loại) |
Theo bảng trên ta có: n = 6
Vậy n = 6 thì a là số nguyên tố.
\(\dfrac{7n-1}{4}\) \(\in\) N ; \(\dfrac{5n+3}{12}\) \(\in\) N
⇔ \(\left\{{}\begin{matrix}7n-1⋮4\\5n+3⋮12\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}3.\left(7n-1\right)⋮12\\5n+3⋮12\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}21n-3⋮12\\5n+3⋮12\end{matrix}\right.\)
⇒ 21n - 3 + 5n + 3 ⋮ 12
(21n + 5n) ⋮ 12
26n ⋮ 12
13n ⋮ 6
n ⋮ 6
⇒ 7n là số chẵn ⇒ 7n - 1 là số lẻ nên 7n - 1 không chia hết cho 4
Vậy không tồn tại số tự nhiên n nào thỏa mãn đề bài.

\(S=\dfrac{1}{1!}+\dfrac{1}{2!}+....+\dfrac{1}{2001!}\)
\(S=1+\dfrac{1}{2!}+\dfrac{1}{3!}+.....+\dfrac{1}{2001!}\)
\(\dfrac{1}{2!}=\dfrac{1}{1\times2};\dfrac{1}{3!}< \dfrac{1}{2\times3};...;\dfrac{1}{2001!}< \dfrac{1}{2000\times2001}\)
\(\dfrac{1}{2!}+\dfrac{1}{3!}+....+\dfrac{1}{2001!}< \dfrac{1}{1\times2}+\dfrac{1}{2\times3}+....+\dfrac{1}{2000\times2001}\)
\(S< 1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2000}-\dfrac{1}{2001}\)
\(S< 2-\dfrac{1}{2001}< 2< 3\)
=> \(S< 3\)

A = \(\dfrac{2023^{2024^{2025}}-2017^{2024^{2023}}}{10}\)
A = \(\dfrac{2023^{2^{2025}.1012^{2025}}-2017^{2^{2023}.1012^{2023}}}{10}\)
A = \(\dfrac{2023^{2^2.2^{2023}.1012^{2025}}-2017^{2^2.2^{2021}1012^{2023}.}}{10}\)
A = \(\dfrac{2023^{4.2^{2023}.1012^{2025}}-2017^{4.2^{2021}.1012^{2023}}}{10}\)
A = \(\dfrac{\left(2023^4\right)^{2^{2023}.1012^{2025}}-\left(2017^4\right)^{2^{2021}.1012^{2023}}}{10}\)
A = \(\dfrac{\left(\overline{..1}\right)^{2^{2023}.1012^{2025}}-\left(\overline{..1}\right)^{2^{2021}.1012^{2023}}}{10}\)
A = \(\dfrac{\overline{..1}-\overline{..1}}{10}\)
A = \(\dfrac{\overline{..0}}{10}\)
A \(\in\) N (đpcm)

A = \(\dfrac{2023^{2024^{2025}}-2017^{2024^{2023}}}{10}\)
A = \(\dfrac{2023^{2^{2025}.1012^{2025}}-2017^{2^{2023}.1012^{2023}}}{10}\)
A = \(\dfrac{2023^{2^2.2^{2023}.1012^{2025}}-2017^{2^2.2^{2021}1012^{2023}.}}{10}\)
A = \(\dfrac{2023^{4.2^{2023}.1012^{2025}}-2017^{4.2^{2021}.1012^{2023}}}{10}\)
A = \(\dfrac{\left(2023^4\right)^{2^{2023}.1012^{2025}}-\left(2017^4\right)^{2^{2021}.1012^{2023}}}{10}\)
A = \(\dfrac{\left(\overline{..1}\right)^{2^{2023}.1012^{2025}}-\left(\overline{..1}\right)^{2^{2021}.1012^{2023}}}{10}\)
A = \(\dfrac{\overline{..1}-\overline{..1}}{10}\)
A = \(\dfrac{\overline{..0}}{10}\)
A \(\in\) N (đpcm)

\(5x+xy-4y=3\)
\(\Rightarrow x\left(y+5\right)-4y-20=3-20\)
\(\Rightarrow x\left(y+5\right)-4\left(y+5\right)=-17\)
\(\Rightarrow\left(y+5\right)\left(x-4\right)=-17\)
Bổ sung: \(x,y\in Z\)
Ta có bảng:
| y + 5 | -1 | 1 | 17 | -17 |
| x - 4 | 17 | -17 | -1 | 1 |
| y | -6 | -4 | 12 | -22 |
| x | 21 | -13 | 3 | 5 |
Vậy: ...
\(5x+xy-4y=3\)
\(\Rightarrow x\cdot\left(y+5\right)-4y-20=3-20\)
\(\Rightarrow x\cdot\left(y+5\right)-4\cdot\left(y+5\right)=-17\)
\(\Rightarrow\left(y+5\right)\cdot\left(x-4\right)=-17\)
\(\Leftrightarrow x,y\in Z\)
Lập bảng giá trị:
| \(y+5\) | \(-1\) | \(1\) | \(17\) |
\(-17\) |
| \(x-4\) | \(17\) | \(-17\) | \(-1\) |
\(1\) |
| \(y\) | \(-6\) | \(-4\) | \(12\) |
\(-22\) |
| \(x\) | \(21\) | \(-13\) | \(3\) |
\(5\) |
Vậy \(\left(x;y\right)\in\left\{\left(21;-6\right),\left(-13;-4\right),\left(3;12\right),\left(5;-22\right)\right\}\)
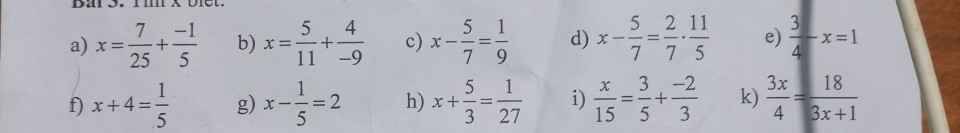
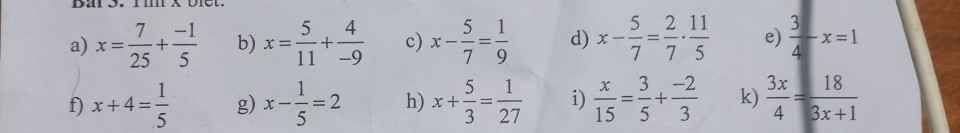

1.2.3.4.5.6.7.8.9 - 1.2.3.4.5.6.7.8 - 1.2.3.4.5.6.7 - 8²
= 1.2.3.4.5.6.7.(8.9 - 8 - 1) - 64
= 5040.63 - 64
= 317520 - 64
= 317456
\(1\times2\times3\times4\times5\times6\times7\times8\times9-1\times2\times3\times4\times5\times6\times7\times8-1\times2\times3\times4\times5\times6\times7-8^2\)
\(=1\times2\times3\times4\times5\times6\times7\times\left(8\times9-8-1\right)-64\)
\(=5040\times63-64\)
\(=317520-64\)
\(=317456\)