E = (1/1+2 - 1)(1/1+2+3 -1)(1/1+2+3+4 -1)...(1/1+2+...+2024 -1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
5 tháng 5
Đây là dạng toán nâng cao chuyên đề lập số theo điều kiện cho trước, cấu trúc thi học sinh giỏi, thi chuyên, thi violympic. Hôm nay, Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Chữ số hàng trăm hơn chữ số hàng đơn vị là: 4 + 4 = 8 (đơn vị)
Vì chữ số hàng đơn vị lớn hơn không nên chữ số hàng trăm lớn hơn:
8 + 0 = 8
Vậy chữ số hàng trăm là 9.
Chữ số hàng chục là: 9 - 4 = 5
Chữ số hàng đơn vị là: 5 - 4 = 1
Số có 3 chữ số thỏa mãn đề bài là: 951
Đáp số: 951
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 5
Gọi A là giao điểm của (d') và Ox, tọa độ A là nghiệm:
\(\left\{{}\begin{matrix}y=2x-1\\y=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2x-1=0\\y=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=0\end{matrix}\right.\)
\(\Rightarrow A\left(\dfrac{1}{2};0\right)\)
Để (d) cắt (d') tại 1 điểm trên trục hoành \(\Rightarrow A\) thuộc (d)
Thay tọa độ A vào pt (d) ta được:
\(\dfrac{1}{2}.\left(2m-1\right)+3=0\)
\(\Rightarrow2m+5=0\Rightarrow m=-\dfrac{5}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 5
Đề bài thiếu rồi em, ko có độ dài BC thì ko thể chứng minh tam giác này vuông
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
5 tháng 5
Đây là dạng toán nâng cao chuyên đề sự tăng giảm diện tích. Cấu trúc thi chuyên, thi học sinh giỏi, thi violympic. Hôm nay, Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Chiều rộng của hình chữ nhật là:
72 : 8 = 9 (m)
Chiều dài của hình chữ nhật là:
9 + 15 = 24 (m)
Diện tích của hình chữ nhật là:
9 x 24 = 216 (m2)
Đáp số: 216 m2
5 tháng 5
a: Xét ΔCAD vuông tại A và ΔCHD vuông tại H có
CD chung
\(\widehat{ACD}=\widehat{HCD}\)
Do đó: ΔCAD=ΔCHD
=>CA=CH
b: Ta có: ΔCAD=ΔCHD
=>DA=DH
=>D nằm trên đường trung trực của AH(1)
Ta có: CA=CH
=>C nằm trên đường trung trực của AH(2)
Từ (1),(2) suy ra CD là đường trung trực của AH
=>CD\(\perp\)AH tại I và I là trung điểm của AH
c: GI=1/2GB
=>BG=2GI
=>\(\dfrac{BG}{BI}=\dfrac{2}{3}\)
Xét ΔHAB có
BI là đường trung tuyến
\(BG=\dfrac{2}{3}BI\)
Do đó: G là trọng tâm của ΔHAB
Xét ΔHAB có
G là trọng tâm
K là trung điểm của AB
DO đó: H,K,G thẳng hàng
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
5 tháng 5
Olm chào em, đây là dạng toán nâng cao hai tỉ số, cấu trúc thi chuyên, thi học sinh giỏi, thi violympic. Hôm nay Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Bước 1: từ hai tỉ số tìm ra tỉ số số cam và số quýt
Bước 2: từ hai tỉ số tìm được ở bước 1 kết hợp với tổng trở thành toán tổng tỉ. Giải toán tổng tỉ thông thường tìm được số cam, số quýt lúc đầu mỗi loại.
Giải:
Số cam còn lại bằng: 1 - \(\dfrac{2}{3}\)= \(\dfrac{1}{3}\) (số cam lúc đầu)
Theo bài ra ta có: \(\dfrac{1}{3}\) số cam lúc đầu = \(\dfrac{1}{4}\) số quýt lúc đầu
Tỉ số số cam lúc đầu và số quýt lúc đầu là: \(\dfrac{1}{4}\): \(\dfrac{1}{3}\) = \(\dfrac{3}{4}\)
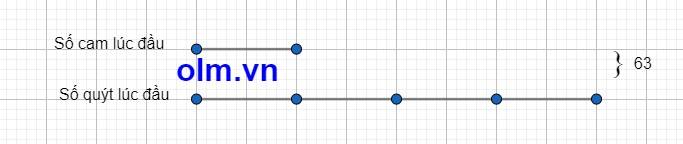
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Số cam lúc đầu là: 63 : (3 + 4) x 3 = 27 (quả)
Số quýt lúc đầu là: 63 - 27 = 36 (quả)
Đáp số: số cam lúc đầu là 27 quả
số quýt lúc đầu là 36 quả
5 tháng 5
a: Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
AH=AE
Do đó: ΔAHD=ΔAED
=>\(\widehat{HAD}=\widehat{EAD}\)
=>AD là phân giác của góc HAC
b: ΔAHD=ΔAED
=>DH=DE
Xét ΔDHK vuông tại H và ΔDEC vuông tại E có
DH=DE
\(\widehat{HDK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDHK=ΔDEC
=>DK=DC
=>ΔDKC cân tại D
AT
1
5 tháng 5
a: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
Do đó: ΔABC=ΔADC
b: Xét ΔACD vuông tại A và ΔAEB vuông tại A có
AC=AE
AD=AB
Do đó: ΔACD=ΔAEB
=>\(\widehat{ACD}=\widehat{AEB}\)
=>CD//EB
c:
Xét ΔBCE có
BA là đường cao
BA là đường trung tuyến
Do đó ΔBCE cân tại B
=>BC=BE
Xét ΔDBC có
I,A lần lượt là trung điểm của CD,DB
=>IA là đường trung bình của ΔDBC
=>\(IA=\dfrac{CB}{2}\)
=>CB=2IA
mà CB=BE
nên BE=2IA