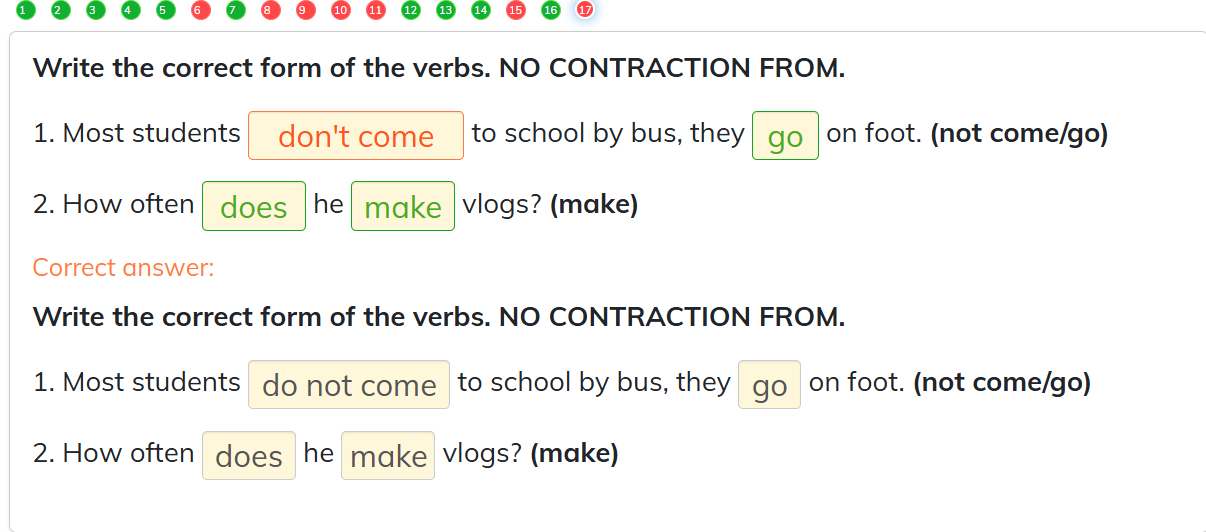
Compelet the second sentence so that it has the same meaning as the first.
1. Would you like to sit down with us?
=> Do you........
2. Kelly is standing in front of Daisy
=> Daisy..........
3. My new school has lots of students.
=> There are......
4. The cupboard is under te stairs.
=> The stairs.........
5. What type of house do you like best?
=> What is.............
6. Does your new flat have many rooms?
=> Are there..........
7. The cat has a black nose.
=> The cat..........
8. The girl has long brown hair.
=> The girl's hair..............




1. Would you like to sit down with us? => Do you.......like sitting down with us?.......
2. Kelly is standing in front of Daisy. => Daisy........is standing behind Kelly...............
3. My new school has lots of students. => There are...lots of students in my new school.............
4. The cupboard is under the stairs. => The stairs......are on the cupboard...............
5. What type of house do you like best? => What is.......your favorite type of house?..................
6. Does your new flat have many rooms? => Are there....many rooms in your new flat?....................
7. The cat has a black nose. => The cat's nose is black.....................
8. The girl has long brown hair. => The girl's hair........is long and brown..........