Làm hết cả nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(x^2-36=0\)
\(\Leftrightarrow x^2-6^2=0\)
\(\Leftrightarrow\left(x-6\right)\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-6=0\\x+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-6\end{matrix}\right.\)
Vậy: ...
b) \(x^2-10x+25=0\)
\(\Leftrightarrow x^2-2\cdot x\cdot5+5^2=0\)
\(\Leftrightarrow\left(x-5\right)^2=0\)
\(\Leftrightarrow x-5=0\)
\(\Leftrightarrow x=5\)
Vậy: ...
a) \(x^2-36=0\)
\(\Leftrightarrow x^2=36\)
\(\Leftrightarrow x^2=\left(\pm6\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-6\end{matrix}\right.\)
Vậy \(x\in\left\{6;-6\right\}\)
b) \(x^2-10x+25=0\)
\(\Leftrightarrow x^2-2.x.5+5^2=0\)
\(\Leftrightarrow\left(x-5\right)^2=0\)
\(\Leftrightarrow x-5=0\)
\(\Leftrightarrow x=5\)
Vậy \(x=5\)

(2x - 5) + 17 = 6
2x - 5 = 6 - 17
2x - 5 = - 11
2x = -11 + 5
2x = -6
x = `(-6)/2`
x = -3
(lớp 5 chưa học số âm)
( 2x - 5 ) + 17 = 6
2x - 5 = 6 - 17
2x - 5 = -11
2x = -11 + 5
2x = -6
x = -6 : 2
x = -3

a) \(\left(3x-1\right)\left(x+2\right)-\left(x+2\right)^2\)
\(=\left(3x^2+6x-x-2\right)-\left(x+2\right)^2\)
\(=\left(3x^2+5x-2\right)-\left(x^2+4x+4\right)\)
\(=3x^2+5x-2-x^2-4x-4\)
\(=2x^2+x-6\)
b) \(\left(x-1\right)\left(x+1\right)-\left(x^2-2x+1\right)\)
\(=\left(x^2-1\right)-\left(x^2-2x+1\right)\)
\(=x^2-1-x^2+2x-1\)
\(=2x-2\)
c) \(\left(x-4\right)\left(4+x\right)+2x\left(x-3\right)\)
\(=\left(x-4\right)\left(x+4\right)+2x\left(x-3\right)\)
\(=\left(x^2-16\right)+2x^2-6x\)
\(=x^2-16+2x^2-6x\)
\(=3x^2-6x-16\)
d) \(\left(x-1\right)\left(x^2-1\right)+\left(x+2\right)^3\)
\(=\left(x^3-x-x^2+1\right)+\left(x^3+6x^2+12x+8\right)\)
\(=x^3-x-x^2+1+x^3+6x^2+12x+8\)
\(=2x^3+5x^2+11x+9\)
e) \(\left(2x-1\right)^2-\left(2x-5\right)\left(x+5\right)\)
\(=\left(4x^2-4x+1\right)-\left(2x^2+10x-5x-25\right)\)
\(=\left(4x^2-4x+1\right)-\left(2x^2+5x-25\right)\)
\(=4x^2-4x+1-2x^2-5x+25\)
\(=2x^2-9x+26\)
f) \(\left(3x+1\right)^2-\left(x^2-1\right)\left(x^2+2\right)\)
\(=\left(9x^2+6x+1\right)-\left(x^4+2x^2-x^2-2\right)\)
\(=\left(9x^2+6x+1\right)-\left(x^4+x^2-2\right)\)
\(=9x^2+6x+1-x^4-x^2+2\)
\(=-x^4+8x^2+6x+3\)
g) \(\left(x^2+1\right)^2-\left(x^2-1\right)\left(x^2+2\right)\)
\(=\left(x^4+2x^2+1\right)-\left(x^4+2x^2-x^2-2\right)\)
\(=\left(x^4+2x^2+1\right)-\left(x^4+x^2-2\right)\)
\(=x^4+2x^2+1-x^4-x^2+2\)
\(=x^2+3\)
h) \(\left(2x^2-4\right)^2-\left(2x^2+4\right)^2\)
\(=\left(4x^4-16x^2+16\right)-\left(4x^4+16x^2+16\right)\)
\(=4x^4-16x^2+16-4x^4-16x^2-16\)
\(=-32x^2\)

\(\dfrac{34+17\times14}{16\times36-32}\)
\(=\dfrac{34+\left(17\times2\right)\times7}{16\times36-16\times2}\)
\(=\dfrac{34+34\times7}{16\times\left(36-2\right)}\)
\(=\dfrac{34\times\left(1+7\right)}{34\times16}\)
\(=\dfrac{8}{16}\)
\(=\dfrac{1}{2}\)


a: Trên tia Ox, ta có: OA<OB
nên A nằm giữa O và B
=>OA+AB=OB
=>AB+3=5
=>AB=2(cm)
b: Vì OC và OA là hai tia đối nhau
nên O nằm giữa C và A
Ta có: O nằm giữa C và A
mà OC=OA(=3cm)
nên O là trung điểm của AC
c: TH1: I nằm giữa O và B
=>OI+IB=OB
=>IB+4=5
=>IB=1(cm)
TH2: I nằm trên tia đối của tia OA
I nằm trên tia đối của tia OA
nên I nằm trên tia đối của tia OB
=>O nằm giữa I và B
=>IB=IO+OB=4+5=9(cm)

Lời giải:
Gọi số chia là $a$. Vì số chia luôn lớn hơn số dư nên $a>29$.
Theo bài ra thì: $65a+29< 1980$
$\Rightarrow 65a< 1951$
$\Rightarrow a< 30,02$
Mà $a>29$ nên $a=30$
Vậy số chia là $30$

a: Vì O thuộc tia đối của tia AB
nên A nằm giữa O và B
=>OB=OA+AB=4+6=10(cm)
M là trung điểm của OA
=>\(OM=MA=\dfrac{OA}{2}=\dfrac{4}{2}=2\left(cm\right)\)
N là trung điểm của OB
=>\(ON=NB=\dfrac{OB}{2}=5\left(cm\right)\)
Vì OM<ON
nên M nằm giữa O và N
=>OM+MN=ON
=>MN+2=5
=>MN=3(cm)
b: \(MN=ON-OM=\dfrac{OB-OA}{2}=\dfrac{BA}{2}\)
=>MN không phụ thuộc vào điểm O
c: Gọi số điểm phải lấy thêm là n(điểm)
Tổng số điểm trên đoạn thẳng AB lúc này là n+2(điểm)
Số tam giác tạo thành là \(C^2_{n+2}\left(tamgiác\right)\)
Theo đề, ta có: \(C^2_{n+2}=465\)
=>\(\dfrac{\left(n+2\right)!}{\left(n+2-2\right)!\cdot2!}=465\)
=>(n+1)(n+2)=930
=>\(n^2+3n-928=0\)
=>\(\left[{}\begin{matrix}n=29\left(nhận\right)\\n=-32\left(loại\right)\end{matrix}\right.\)
Vậy: Số điểm phải lấy thêm là 29 điểm
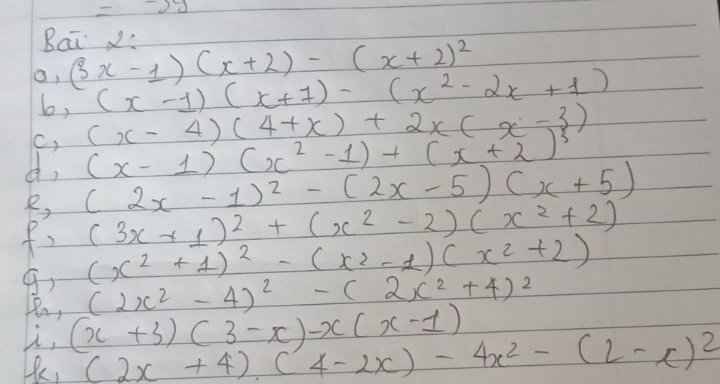

 giup em bai nay a kho qua
giup em bai nay a kho qua
a: Xét ΔBAD vuông tại A và ΔBMD vuông tại M có
BD chung
\(\widehat{ABD}=\widehat{MBD}\)
Do đó: ΔBAD=ΔBMD
b: ΔBAD=ΔBMD
=>DA=DM
mà DM<DC(ΔDMC vuông tại M)
nên DA<DC
c: ΔBAD=ΔBMD
=>BA=BM
=>ΔBAM cân tại B
Ta có: ΔBAM cân tại B
mà BI là đường phân giác
nên BI\(\perp\)AM và I là trung điểm của AM
Ta có: BI\(\perp\)AM
ME\(\perp\)AM
Do đó: ID//ME
Xét ΔAME có
I là trung điểm của AM
ID//ME
Do đó: D là trung điểm của AE
Xét ΔAME có
AK,EI,MD là các đường trung tuyến
Do đó: AK,EI,MD đồng quy