 Giúp mình câu c) ạ !
Giúp mình câu c) ạ !
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
c: \(C=27x^3-27x^2y+9xy^2-y^3-121\)
\(=\left(3x\right)^3-3\cdot\left(3x\right)^2\cdot y+3\cdot3x\cdot y^2-y^3-121\)
\(=\left(3x-y\right)^3-121=7^3-121=343-121=222\)
Bài 3:
a: \(x^2-4+\left(x-2\right)^2\)
\(=\left(x-2\right)\left(x+2\right)+\left(x-2\right)^2\)
=(x-2)(x+2+x-2)
=2x(x-2)
b: \(x^3-2x^2+x-xy^2\)
\(=x\left(x^2-2x+1-y^2\right)\)
\(=x\left[\left(x-1\right)^2-y^2\right]=x\left(x-1-y\right)\left(x-1+y\right)\)
c: \(x^3-4x^2-12x+27\)
\(=\left(x^3+27\right)-4x\left(x+3\right)\)
\(=\left(x+3\right)\left(x^2-3x+9\right)-4x\left(x+3\right)\)
\(=\left(x+3\right)\left(x^2-7x+9\right)\)
d: \(\left(x^2+x\right)^2-2\left(x^2+x\right)-15\)
\(=\left(x^2+x\right)^2-5\left(x^2+x\right)+3\left(x^2+x\right)-15\)
\(=\left(x^2+x\right)\left(x^2+x-5\right)+3\left(x^2+x-5\right)\)
\(=\left(x^2+x-5\right)\left(x^2+x+3\right)\)


Câu 8:
\(x:4\times36-x:7\times28+x:4\times20=180\)
=>9x-4x+5x=180
=>10x=180
=>x=180:10=18

a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)(hai góc so le trong, AD//CB)
Do đó: ΔAHD=ΔCKB
=>AH=CK
Ta có: AH\(\perp\)BD
CK\(\perp\)BD
Do đó: AH//CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó:AHCK là hình bình hành
b: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
ta có: AHCK là hình bình hành
=>AC cắt HK tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của HK
c: Xét tứ giác AMCN có
AM//CN
AN//CM
Do đó: AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MN
=>M,O,N thẳng hàng


Để hệ có nghiệm duy nhất thì \(\dfrac{a+1}{1}\ne\dfrac{-a}{a}=-1\)
=>\(a+1\ne-1\)
=>\(a\ne-2\)
\(\left\{{}\begin{matrix}\left(a+1\right)x-ay=5\\x+ay=a^2+4a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(a+1\right)x-ay+x+ay=5+a^2+4a\\x+ay=a^2+4a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\left(a+2\right)=a^2+4a+5\\ay=a^2+4a-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{a^2+4a+5}{a+2}\\ay=a^2+4a-\dfrac{a^2+4a+5}{a+2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{a^2+4a+5}{a+2}\\ay=\dfrac{\left(a+2\right)\left(a^2+4a\right)-a^2-4a-5}{a+2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{a^2+4a+5}{a+2}\\y=\dfrac{a^3+4a^2+2a^2+8a-a^2-4a-5}{a\left(a+2\right)}=\dfrac{a^3+5a^2+4a-5}{a\left(a+2\right)}\end{matrix}\right.\)
Để x,y nguyên thì \(\left\{{}\begin{matrix}a^2+4a+5⋮a+2\\a^3+5a^2+4a-5⋮a^2+2a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a^2+4a+4+1⋮a+2\\a^3+5a^2+4a-5⋮a^2+2a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1⋮a+2\\a^3+5a^2+4a-5⋮a^2+2a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a+2\in\left\{1;-1\right\}\\a^3+5a^2+4a-5⋮a^2+2a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a\in\left\{-1;-3\right\}\\a^3+5a^2+4a-5⋮a^2+2a\end{matrix}\right.\Leftrightarrow a=-1\)

\(\left|\dfrac{4}{3}x-\dfrac{1}{4}\right|>=0\forall x\)
=>\(A=\left|\dfrac{4}{3}x-\dfrac{1}{4}\right|-\dfrac{2}{11}>=-\dfrac{2}{11}\forall x\)
Dấu '=' xảy ra khi \(\dfrac{4}{3}x-\dfrac{1}{4}=0\)
=>\(\dfrac{4}{3}x=\dfrac{1}{4}\)
=>\(x=\dfrac{1}{4}:\dfrac{4}{3}=\dfrac{3}{16}\)

a: 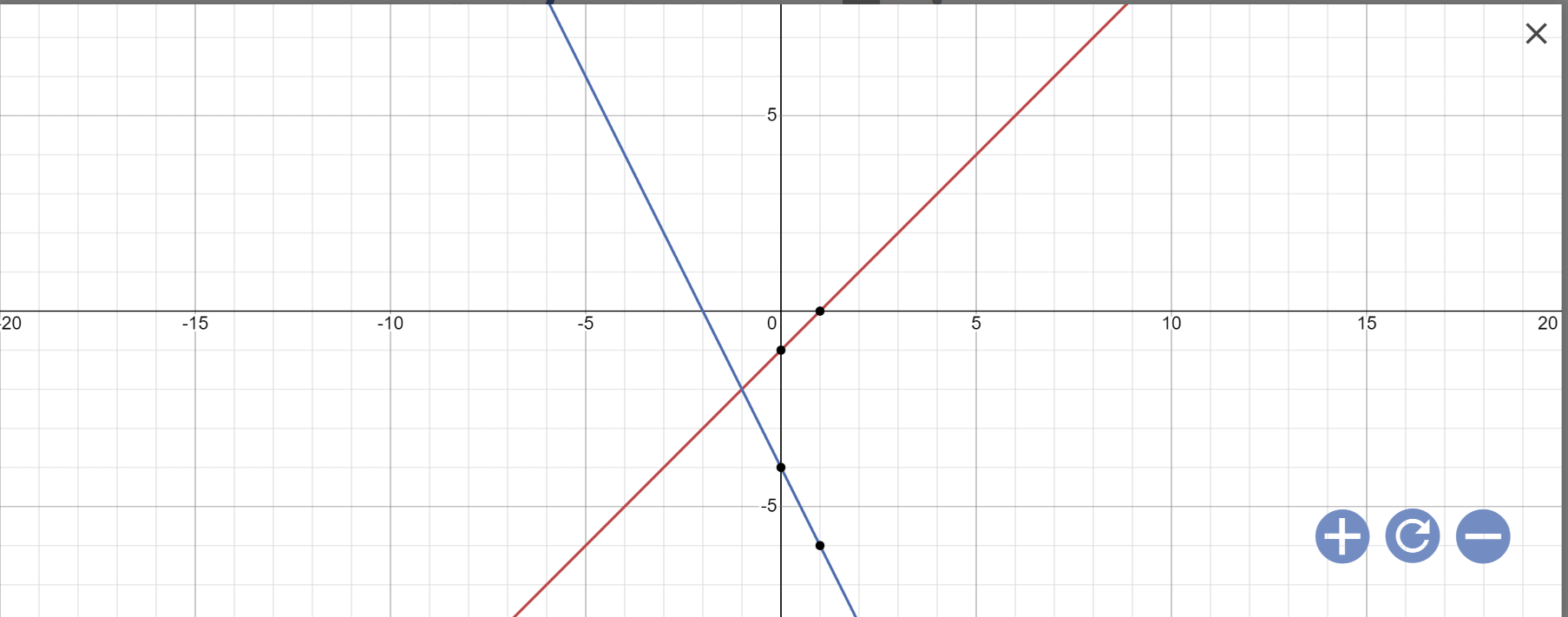
b: Phương trình hoành độ giao điểm là:
-2x-4=x-1
=>-2x-x=-1+4
=>-3x=3
=>x=-1
Thay x=-1 vào y=x-1, ta được:
y=-1-1=-2
Vậy: Tọa độ giao điểm là A(-1;-2)

\(\left|6x+22\right|>=0\forall x;\left(y-21\right)^2>=0\forall y\)
Do đó: \(\left|6x+22\right|+\left(y-21\right)^2>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}6x+22=0\\y-21=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{11}{3}\\y=21\end{matrix}\right.\)


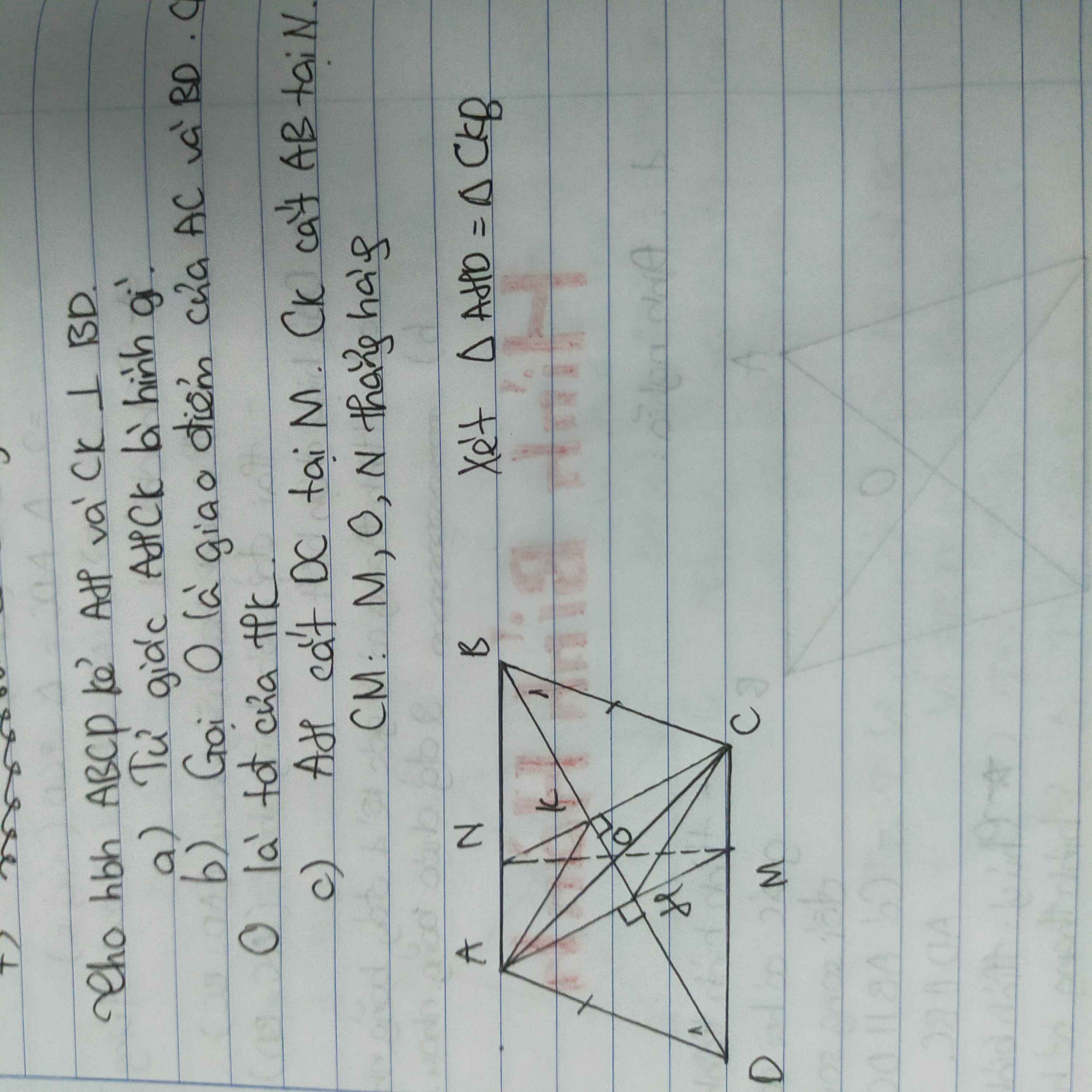


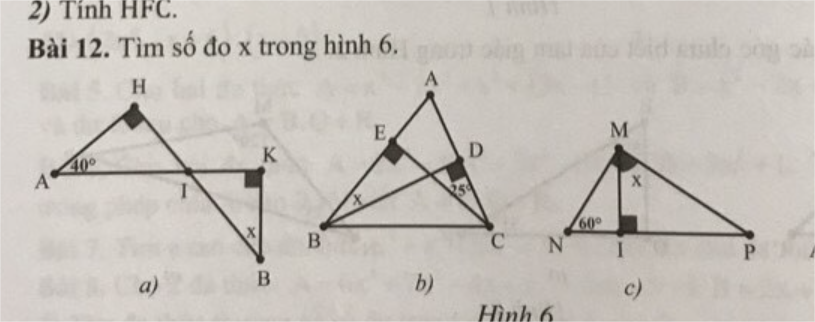
a: Ta có: \(\widehat{HIA}+\widehat{HAI}=90^0\)(ΔHAI vuông tại H)
\(\widehat{KIB}+\widehat{KBI}=90^0\)(ΔKIB vuông tại K)
mà \(\widehat{HIA}=\widehat{KIB}\)(hai góc đối đỉnh)
nên \(\widehat{HAI}=\widehat{KBI}\)
=>\(x=40^0\)
b: Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BEDC là tứ giác nội tiếp
=>\(x=\widehat{EBD}=\widehat{ECD}=35^0\)
c: Ta có: \(\widehat{IMP}+\widehat{IPM}=90^0\)(ΔMIP vuông tại I)
\(\widehat{MPN}+\widehat{MNP}=90^0\)(ΔMNP vuông tại M)
Do đó: \(x=\widehat{IMP}=\widehat{N}=60^0\)