Cho bàn cờ \(C\) bất kỳ gồm \(m\) hàng và \(n\) cột, đa thức quân xe của bàn cờ \(C\) được định nghĩa như sau:
\(R\left(C,x\right)=r_0\left(C\right)+r_1\left(C\right)x+...+r_k\left(C\right)x^k+...=\sum\limits^{\infty}_{k=0}r_k\left(C\right)x^k\)
trong đó \(r_k\left(C\right)\) là số cách xếp \(k\) con xe không "ăn nhau" trên bàn cờ \(C\).
a) Gọi \(C_d,C_c\) là bàn cờ tương ứng có được khi đổi chỗ hai dòng bất kì và hai cột bất kì của \(C\). Chứng minh rằng \(R\left(C,x\right)=R\left(C_d,x\right)=R\left(C_c,x\right)\)
b) Hai bàn cờ \(A,B\) gọi là hai bàn cờ độc lập nếu không có ô vuông vào của A và B chung hàng hoặc chung cột. VD trong hình thì A và B là hai bàn cờ độc lập:
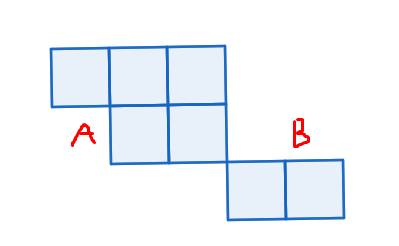
Chứng minh rằng nếu A, B là hai bàn cờ độc lập thì \(R\left(A\cup B,x\right)=R\left(A,x\right).R\left(B,x\right)\)
c) Ta gọi một miền ô vuông \(S\) của \(C\) là block của bàn cờ \(C\) nếu thỏa mãn các điều kiện sau:
i) Với bất kì hai dòng \(i,i'\) chứa ô của \(S\) và cột \(j\) không chứa ô nào của \(S\) thì hai ô \(\left(i;j\right)\) và \(\left(i';j\right)\) hoặc cùng là ô vuông của \(C\) hoặc không cùng là ô vuông của \(C\).
ii) Với bất kì hai cột \(j,j'\) chứa ô của \(S\) và dòng \(i\) không chứa ô nào của \(S\) thì hai ô \(\left(i;j\right)\) và \(\left(i;j'\right)\) hoặc cùng là ô vuông của \(C\) hoặc không cùng là ô vuông của \(C\).
(Lưu ý: Nếu \(C\) là bàn cờ gồm các ô vuông thì mỗi ô vuông của \(C\) được xem là một block của \(C\))
Ví dụ trong hình thì vùng màu cam là block của bàn cờ \(C\):
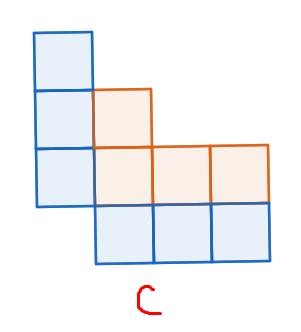
Cho \(C\) là bàn cờ các ô vuông có block S nằm trên \(m\) dòng và \(n\) cột, đặt \(p=min\left\{m,n\right\}\). Với mỗi \(0\le k\le p\), kí hiệu \(D_k\left(S\right)\) là bàn cờ có được từ bàn cờ \(C\) sau khi thực hiện các bước sau:
1. Bỏ tất cả các ô của \(S\).
2. Bỏ tất cả các ô thuộc \(k\) dòng tùy ý trong số \(m\) dòng của \(S\).
3. Bỏ tất cả các ô thuộc \(k\) cột tùy ý trong số \(n\) cột chứa các ô của \(S\).
Chứng minh rằng đa thức quân xe của bàn cờ \(C\) là:
\(R\left(C,x\right)=\sum\limits^p_{k=0}r_k\left(S\right)x^kR\left(D_k\left(S\right),x\right)\).




