\(\sqrt{15-\sqrt{216}+\sqrt{33-12\sqrt{6}}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(sina=\dfrac{12}{13}\\ \Rightarrow cosa=\sqrt{1-\left(\dfrac{12}{13}\right)^2}=\dfrac{5}{13}\\ tana=\dfrac{sina}{cosa}=\dfrac{\dfrac{12}{13}}{\dfrac{5}{13}}=\dfrac{12}{5}\)

\(2\sqrt{5}-\sqrt{125}+\sqrt{80}+\sqrt{605}\)
\(=2\sqrt{5}-5\sqrt{5}+4\sqrt{5}+11\sqrt{5}\)
\(=\left(2-5+4+11\right)\sqrt{5}\)
\(=12\sqrt{5}\)

Cái này chiều nay bọn mình vừa được học xong.
Định luật Ôm : Cường độ dòng điện chạy qua dây dẫn tỉ lệ thuận với hiệu điện thế được mắc ở hai đầu dây và tỉ lệ nghịch với điện trở của dây dẫn : \(I\text{=}\dfrac{U}{R}\)

\(2\sqrt[]{37+20\sqrt[]{3}}-\sqrt[]{73-40\sqrt[]{3}}\)
\(=2\sqrt[]{25+2.5.2\sqrt[]{3}+12}-\sqrt[]{48-2.5.4\sqrt[]{3}+25}\)
\(=2\sqrt[]{\left(5+2\sqrt[]{3}\right)^2}-\sqrt[]{\left(5-4\sqrt[]{3}\right)^2}\)
\(=2\left|5+2\sqrt[]{3}\right|-\left|5-4\sqrt[]{3}\right|\)
\(=2\left(5+2\sqrt[]{3}\right)-\left(4\sqrt[]{3}-5\right)\left(vì.4\sqrt[]{3}>5\right)\)
\(=10+4\sqrt[]{3}-4\sqrt[]{3}+5\)
\(=15\)

\(R_B=3R_A\)
Chu vi hình tròn A : \(C_A=2\pi R_A\)
Chu vi hình tròn B : \(C_B=2\pi R_B=2\pi.3R_A=3C_A\)
Vậy hình A lăn xung quanh hình B, nó phải quay 3 vòng để trở lại điểm xuất phát
Mặc dù B gấp 3 lần bán kính A nhưng quãng đường mà đường tròn A lăn không phải là chu vi của B mà là hình tròn có tổng bán kính của A và B.
Bán kính của hình tròn A phải lăn gấp bán kính của A số lần là:
\(\left(3+1\right)=4\left(lần\right)\)
Vậy A sẽ phải mất số vòng quay là:
\(\dfrac{4\pi}{1\pi}=4\) (vòng)

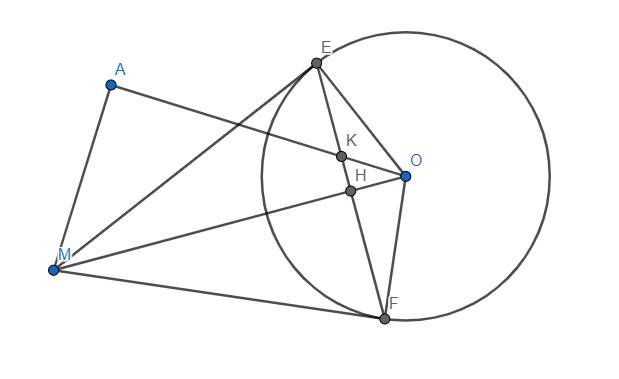
a) Ta thấy \(OE=OF\Rightarrow\) O thuộc trung trực của EF.
Mặt khác, theo tính chất của 2 tiếp tuyến cắt nhau, \(ME=MF\), suy ra M cũng nằm trên trung trực của EF.
\(\Rightarrow\)OM là trung trực của EF. Mà OM cắt EF tại H nên H là trung điểm EF (đpcm)
b) Ta thấy \(\widehat{OAM}+\widehat{OFM}=90^o+90^o=180^o\) nên tứ giác OAMF nội tiếp hay 4 điểm O, M, A, F cùng thuộc 1 đường tròn.
c) Vì OM là trung trực EF nên \(OM\perp EF\) tại H \(\Rightarrow\widehat{MHK}=90^o\)
Từ đó dễ thấy tứ giác AMHK nội tiếp \(\Rightarrow OA.OK=OH.OM\)
Mà \(OH.OM=OE^2=R^2\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow OA.OK=R^2\) (đpcm)
yêu cầu ?
= 2 căn 6 - 3 + 3 - căn 6
= căn 6
Cho mình xin 1 tick nha trang