
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Olm chào em, Số chẵn bên tay phải và số lẻ ở bên tay trái em nhé.

A = \(x^2\) + 5\(x\) - 6
A = \(x^2\) - \(x\) + 6\(x\) - 6
A = (\(x^2\) - \(x\)) + (6\(x\) - 6)
A = \(x\).(\(x-1\)) + 6.(\(x-1\))
A = (\(x\) - 1).(\(x\) + 6)

27 x 37 + 27 x 63
= 27 x (37 + 63)
= 27 x 100
= 2700

Tự vẽ hình nhé.
a) Theo bài ra ABCD là HCN
=> AD=BC (1) ; AD//BC
Do AD//BC => ADB=DBC (2 góc so le trong) hay ADN=CBM (2)
Ta có AN vuông góc với BD => AND=ANB=90
CM vuông góc với BD => CMD=CMB=90
Xét tam giác AND và tam giác CMB có
AND=CMB=90
AD=BC ( theo (1) )
ADN = CBM ( theo (2) )
=> tam giác AND= tam giác CMB (cạnh huyền-góc nhọn)
=> ND = MB (2 cạnh tương ứng) (dpcm)
b) Do AN vuông góc với BD và CM vuông góc với BD
=>AN//CM (mối quan hệ từ vuông góc đến song song)
Lại có: tam giác AND= tam giác CMB (cạnh huyền-góc nhọn)
=> AN = CM (2 cạnh tương ứng)
Xét tứ giác ANCM có AN=CM và AN//CM
=> tứ giác ANCM là hình bình hành.
c) Lại thấy AN//CM => KN // CM
Xét tứ giác KCMN có KN=CM và KN // CM
=> tứ giác KCMN là hình bình hành
=> KC // MN
=> KC//BD
Xét tứ giác DKCB có KC//BD => tứ giác DKCB là hình thang.
d) Do K là điểm đối xứng với A qua N
=>NA=NK
=> N là trung điểm của AK.
=>PN là đường trung tuyến của tam giác AKP.
Mặt khác KC//MN => CP//MB => BMP= MPC (2 góc so le trong)
Mà AMN=BMP (2 góc đồng vị)
Từ đó suy ra AMN=MPC
Vì ANM=90 nên tam giác ANM vuông tại N
=> NAM +AMN = 90
Vì MC vuông góc với BD mà BD//CP
=> MC vuông góc với CP (mqh..)
=> MCP = 90 => tam giác MCP vuông tại C => CMP+MPC=90
Do đó NAM + AMN = CMP + MPC = 90
Mà AMN=MPC
=> NAM = CMP
Xét tam giác ANM và tam giác MCP có
NAM = CMP (theo cmt)
AN=CM (từ phần b)
ANM=MCP(=90)
=> tam giác ANM = tam giác MCP (cạnh huyền-cạnh góc vuông)
=> AN=MP( 2 cạnh tương ứng)
và MN =CP ( 2 cạnh tương ứng)
Vì MN=CK và MN=CP
=> CK=CP
=> C là trung điểm của PK
=>AC là đường trung tuyến của tam giác AKP.
Do AM=MP => M là trung điểm của AP
=>KM là đường trung tuyến của tam giác AKP.
Xét tam giác AKP có PN là đường trung tuyến của tam giác AKP.
AC là đường trung tuyến của tam giác AKP.
KM là đường trung tuyến của tam giác AKP.
Từ đó suy ra PN, AC, KM đồng quy tại trọn tâm của tam giác AKP
Vậy..

Công thức E=mc2E = mc^2E=mc2 là phương trình nổi tiếng của nhà vật lý học Albert Einstein. Phương trình này là một phần của thuyết tương đối hẹp và diễn tả mối quan hệ giữa năng lượng (E), khối lượng (m), và tốc độ ánh sáng trong chân không (c). Cụ thể:
- EEE là năng lượng.
- mmm là khối lượng.
- ccc là tốc độ ánh sáng trong chân không, xấp xỉ 3×1083 \times 10^83×108 mét/giây.
Phương trình này cho thấy rằng khối lượng và năng lượng có thể hoán đổi cho nhau, nghĩa là một vật có khối lượng nhỏ cũng có thể chứa một lượng năng lượng khổng lồ. Điều này đã có những ứng dụng quan trọng trong nhiều lĩnh vực của vật lý, bao gồm cả việc giải thích năng lượng giải phóng trong phản ứng hạt nhân.
Albert Einstein đã công bố thuyết tương đối hẹp vào năm 1905 trong bài báo mang tên "Zur Elektrodynamik bewegter Körper" (Về điện động lực học của các vật chuyển động). Phương trình nổi tiếng E=mc2E = mc^2E=mc2 xuất hiện trong một bài báo tiếp theo vào năm 1905 với tiêu đề "Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?" (Sự quán tính của một vật có phụ thuộc vào năng lượng của nó không?).

a:
| Giai đoạn | Quý I/2020 | Quý I/2021 | Quý I/2022 |
| Xuất khẩu | 63,4 | 78,56 | 89,1 |
| Nhập khẩu | 59,59 | 76,1 | 87,64 |
b:
| Giai đoạn | Quý I/2020 | Quý I/2021 | Quý I/2022 |
| Tỉ số giữa xuất và nhập | 1,06 | 1,03 | 1,01 |
c: Tổng trị giá xuất khẩu của nước ta trong quý I giai đoạn 2020-2022 là:
63,4+78,56+89,1=231,06(tỉ USD)
d: Tổng trị giá nhập khẩu của nước ta trong quý I giai đoạn 2020-2022 là:
59,59+76,1+87,64=223,33(tỉ USD)
e: Trị giá xuất khẩu trong quý I/2020 so với quý I/2021 thì giảm:
\(\dfrac{78,56-63,4}{63,4}\simeq23,91\%\)
f: Trị giá nhập khẩu trong quý I/2021 so với quý I/2020 thì tăng:
\(\dfrac{76,1-59,59}{59,59}-100\%\simeq27.71\%\)

a)
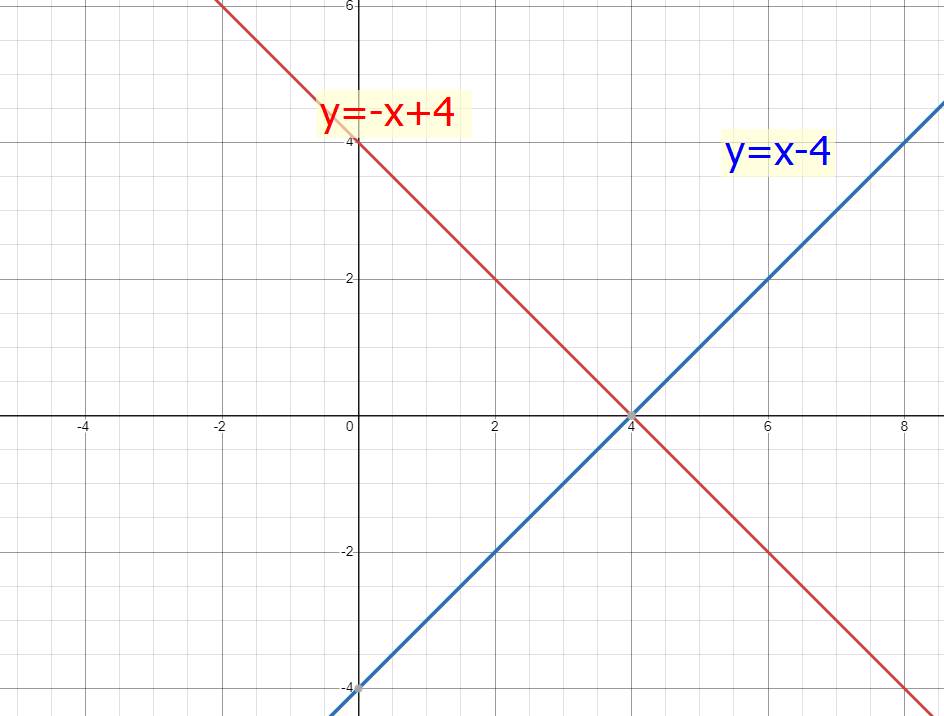
b) Hàm số y=-x+4 cắt Oy tại \(\left(0;4\right)\) \(\Rightarrow A\left(0;4\right)\)
Hàm số y=x-4 cắt Oy tại \(\left(0;-4\right)\) \(\Rightarrow B\left(0;-4\right)\)
Ta có pt hoành độ giao điểm của y=-x+4 và y=x-4 là:
\(-x+4=x-4\Leftrightarrow x=4\)
\(\Rightarrow y=4-4=0\)
\(\Rightarrow C\left(4;0\right)\)
c) Ta có: \(A\left(0;4\right)\Rightarrow OA=4\)
\(B\left(0;-4\right)\Rightarrow OB=4\)
\(C\left(0;4\right)\Rightarrow OC=4\)
BC = OA + OB = 4 + 4 = 8
\(\Rightarrow S_{ABC}=\dfrac{1}{2}\cdot4\cdot8=16\) (đvdt)

a: Xác suất thực nghiệm của biến cố "Thẻ lấy ra ghi số 7" là:
\(\dfrac{6}{30}=\dfrac{1}{5}\)
b: Gọi A là biến cố "Thẻ rút ra là số nguyên tố"
=>A={2;3;5;7;11;13}
=>n(A)=6
=>\(P_A=\dfrac{6}{15}=\dfrac{2}{5}\)
=>Khi số lần rút thẻ ngày càng lớn thì xác suất thực nghiệm của biến cố A ngày càng gần với 2/5


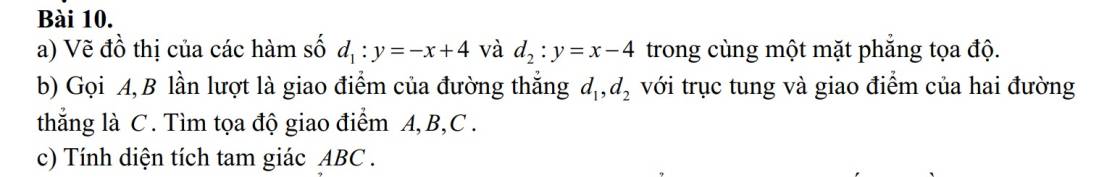
\(\frac{x-1}{1999}+\frac{x-2}{1998}=\frac{x-3}{1997}+\frac{x-4}{1996}\\\Leftrightarrow \left(\frac{x-1}{1999}-1\right) +\left(\frac{x-2}{1998}-1\right)=\left(\frac{x-3}{1997}-1\right)+\left(\frac{x-4}{1996}-1\right)\\\Leftrightarrow \frac{x-2000}{1999}+\frac{x-2000}{1998}=\frac{x-2000}{1997}+\frac{x-2000}{1996}\\\Leftrightarrow \frac{x-2000}{1999}+\frac{x-2000}{1998}-\frac{x-2000}{1997}-\frac{x-2000}{1996}=0\\ \Leftrightarrow (x-2000)\left(\frac{1}{1999}+\frac{1}{1998}-\frac{1}{1997}-\frac{1}{1996}\right)=0\\\Leftrightarrow x-2000=0\left(\text{vì } \frac{1}{1999}+\frac{1}{1998}-\frac{1}{1997}-\frac{1}{1996}\ne0\right)\\\Leftrightarrow x=2000\)
Vậy phương trình đã cho có 1 nghiệm duy nhất là \(x=2000\).
cứu tui với ăng em