Cho tam giác $ABC$ cân tại $A$ và nội tiếp đường tròn tâm $O$, đường kính $AI$. Gọi $E$ là trung điểm của $AB$, $K$ là trung điểm của $OI$, $H$ là trung điểm của $EB$.
a/ Chứng minh  $HK\perp EB$
b/ Chứng minh tứ giác $AEKC$ nội tiếp được trong một đường tròn.

a) Ta thấy E, O là trung điểm của AB và AI nên EO là đường trung bình tam giác ABI

$\Rightarrow$ EO song song với BI.

Ta lại có H, K lần lượt là trung điểm của EB và OI

nên HK là đường trung bình của hình thang EOIB.

=> HK song song với BI (1)

Mặt khác do AI là đường kính nên góc ABI = 90 (2)\widehat{ABI}=90^o

Từ (1) và (2) suy ra $HKvuông\; góc\; vớiEB$(đpcm)

b)

Xét tam giác KBE có KH là trung tuyến đồng thời đường cao (CM trước)

nên KBE là tam giác cân tại K.

=> góc BEK = KBE (3)

Do tam giác ABC cân tại A

nên AI là đường trung trực của BC

Mà K thuộc AI nên KB = KC

hay tam giác KBC cân tại K

=> KBC=KCB 

và ACB=ABC 

$\hat{}$.Mặt khác, ta lại có  ACB=  ACK + KCB và ABC = ABK + KBC

=> ABK=ACK(4)

Từ (3) và (4) suy ra $\hat{}\hat{}$.

 AEKC là tứ giác nội tiếp.

Cho $AB$ và $MN$ là hai đường kính khác nhau của đường tròn $(O)$. Tiếp tuyến tại $B$ của $(O)$ cắt các đường thẳng $AM$, $AN$ lần lượt tại $P$ và $Q$. Chứng minh:

a) $ABMN$ là hình chữ nhật.

b) Bốn điểm $M$, $N$, $P$, $Q$ cùng thuộc một đường tròn.

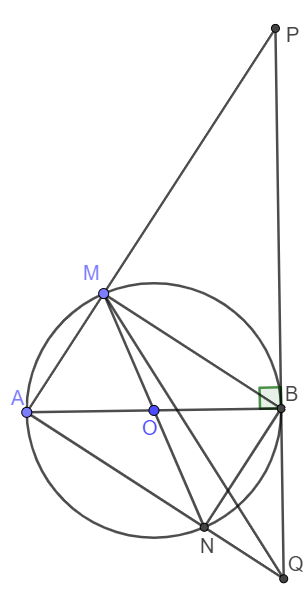
 a) Theo gt, ta có :

 $AB$ và $MN$ là hai đường kính khác nhau của đường tròn $(O)$

$=>\; góc\; MAN=\; MBN=AMB=ANB\; (tính\; chất\; góc\; nội\; tiếp\; nhìn\; nửa\; đường\; tròn)$

$=>\; AMBN\; là\; hình\; chữ\; nhật$(đpcm)

b) Ta thấy:

MNA= MBA (cùng chắn cung MA)

MBA= 90 - PAB (tính chất tổng 3 góc trong tam giác MBA)

MPB= 90 - PAB  (tính chất tổng 3 góc trong tam giác MPB)

=> MNA = MPA => đpcm (vì là tứ giác có góc ngoài tam giác bằng góc đối trong tứ giác)

Cho đường tròn tâm $O$ đường kính $MN$ và $A$ là một điểm trên đường tròn $(O)$, ($A$ khác $M$ và $A$ khác $N$). Lấy một điểm $I$ trên đoạn thẳng $ON$ ($I$ khác $O$ và $I$ khác $N$). Qua $I$ kẻ đường thẳng $(d)$ vuông góc với $MN$. Gọi $P$, $Q$ lần lượt là giao điểm của $AM$, $AN$ với đường thẳng $(d)$. Gọi $K$ là điểm đối xứng của $N$ qua điểm $I$. Chứng minh góc PMK = IQN$\hat{}$ và tứ giác $MPQK$ nội tiếp đường tròn.

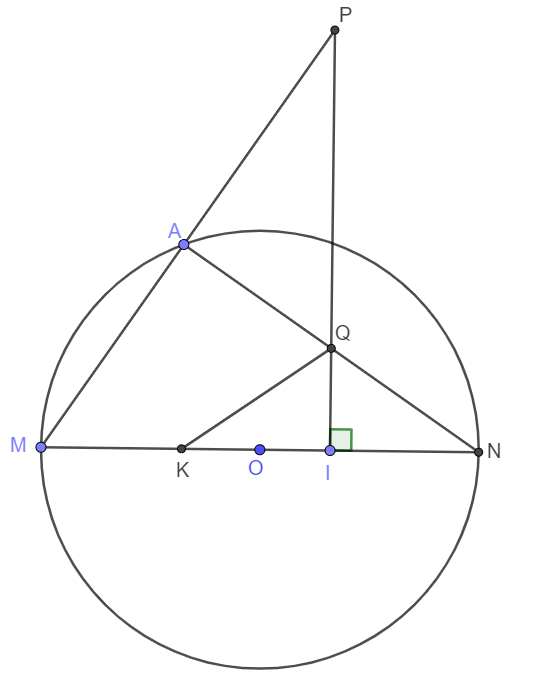
 Xét 2 tam giác AMN và IQN có :

góc A= goc QIN= 90 (gt)

=> goc M= IQN= 90 - goc N (đpcm)

Xet 2 tam giác IQK và IQN có: 

IQ chung

vì $K$ là điểm đối xứng của $N$ qua điểm $I$

$=>\; IK\; =IN$

$góc\; QIK\; =\; QIN=90$

$=>$2 tam giác IQK = IQN (c.g.c)

=> góc IQK=IQN=PQA=PMK

trong đó  góc PQK + IQN = 180

=> góc PQK + PMK = 180

=> đpcm