Ta có \(VT=\dfrac{\dfrac{4x^2}{y^2}}{\left(\dfrac{x^2}{y^2}+1\right)^2}+\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\)

Đặt \(\dfrac{x^2}{y^2}=t\left(t>0\right)\) thì VT thành

\(\dfrac{4t}{\left(t+1\right)^2}+t+\dfrac{1}{t}\)

\(=\dfrac{4t}{\left(t+1\right)^2}+\dfrac{t^2+1}{t}\)

\(=\dfrac{4t}{\left(t+1\right)^2}+\dfrac{\left(t+1\right)^2}{t}-2\)

Đặt \(\dfrac{\left(t+1\right)^2}{t}=u\left(u\ge4\right)\) (vì BĐT \(\left(a+b\right)^2\ge4ab\))

Khi đó \(VT=u+\dfrac{4}{u}-2\)

 \(=\dfrac{4}{u}+\dfrac{u}{4}+\dfrac{3u}{4}-2\)

\(\ge2\sqrt{\dfrac{4}{u}.\dfrac{u}{4}}+\dfrac{3.4}{4}-2\)

\(=2+3-2\)

\(=3\)

\(\Rightarrow VT\ge3\)

Dấu "=" xảy ra \(\Leftrightarrow u=4\) \(\Leftrightarrow t=1\) \(\Leftrightarrow x=\pm y\)

Vậy ta có đpcm. Dấu "=" xảy ra \(\Leftrightarrow x=\pm y\)

câu a

\(\dfrac{3x+15}{x^2-9}+\dfrac{1}{x+3}-\dfrac{2}{x-3}\\ =\dfrac{3\cdot\left(x+5\right)}{\left(x-3\right)\cdot\left(x+3\right)}+\dfrac{1}{x+3}-\dfrac{2}{x-3}\\ =\dfrac{3\cdot\left(x+5\right)}{\left(x-3\right)\cdot\left(x+3\right)}+\dfrac{x-3}{\left(x+3\right)\cdot\left(x-3\right)}-\dfrac{2\cdot\left(x+3\right)}{\left(x-3\right)\cdot\left(x+3\right)}\)\(=\dfrac{3\cdot\left(x+5\right)+x-3-2\cdot\left(x+3\right)}{\left(x-3\right)\cdot\left(x+3\right)}\\ =\dfrac{3x+15+x-3-2x-6}{\left(x-3\right)\cdot\left(x+3\right)}\\ =\dfrac{2x+6}{\left(x+3\right)\cdot\left(x-3\right)}\\ =\dfrac{2\cdot\left(x+3\right)}{\left(x+3\right)\cdot\left(x-3\right)}\\ =\dfrac{2}{x-3}\)

câu b

để \(\dfrac{2}{x-3}=\dfrac{2}{3}\) thì \(x-3=3\)

\(\Rightarrow x=3+3=6\)

vậy  \(x=6\) thì \(A=\dfrac{2}{3}\)

Gọi quãng đường AB là: \(x\left(km,x>0\right)\)

Vận tốc trung bình là 15km/h nên vận tốc lúc về là: \(2\cdot15-12=18\left(km/h\right)\)

Thời gian đi là: \(\dfrac{x}{12}\left(h\right)\)

Thời gian về là: \(\dfrac{x}{18}\left(h\right)\)

Lúc về nhiều hơn lúc đi 45 phút ta có phương trình:

\(\dfrac{x}{12}-\dfrac{x}{18}=\dfrac{3}{4}\) 

\(\Leftrightarrow x\left(\dfrac{1}{12}-\dfrac{1}{18}\right)=\dfrac{3}{4}\)

\(\Leftrightarrow x\cdot\dfrac{1}{36}=\dfrac{3}{4}\)

\(\Leftrightarrow x=\dfrac{3}{4}:\dfrac{1}{36}\)

\(\Leftrightarrow x=27\left(km\right)\)

Vậy: ... 

Gọi x (km) là độ dài quãng đường AB (x > 0)

Thời gian đi là: x/15 (h)

Thời gian về là: x/12 (h)

45 phút = 3/4 (h)

Theo đề bài ta có phương trình:

x/12 - x/15 = 3/4

5x - 4x = 45

x = 45 (nhận)

Vậy quãng đường AB dài 45 km

a,Ta có: đường cao AH 

=> AH vuông góc BC => AHB = 90`

Tam giác ABC vuông tại A

=> ABC = 90`

Xét hai tam giác ABC và HBA có:

• AHB = ABC (=90`)
• chung góc B

=>    Δ ABC ~ Δ HBA (g-g)

=> \(\dfrac{AB}{HB}=\dfrac{BC}{BA}\) ( các cạnh tưng ứng )

​=> AB.BA=HB.BC \(AB^2\) = BC.BH

​Vậy ΔABC ~ ΔHBA ; \(AB^2\)= BC.BH
   

b, 

a,Ta có: đường cao AH 

=> AH vuông góc BC => AHB = 90`

Tam giác ABC vuông tại A

=> ABC = 90`

Xét hai tam giác ABC và HBA có:

• AHB = ABC (=90`)
• chung góc B

=>    Δ ABC ~ Δ HBA (g-g)

=> $\genfrac{}{}{0ex}{}{AB}{HB}=\genfrac{}{}{0ex}{}{BC}{BA}$ ( các cạnh tưng ứng )

​Vậy ΔABC ~ ΔHBA ; $A{B}^2$= BC.BH

a; Hai đường thẳng trên cắt nhau khi và chì khi:

1 ≠ m²

m \(\ne\) -1; 1

Kết luận m ≠ -1; 1 thì hai đường thẳng đã cho cắt nhau. 

b; Hai đường thẳng đã cho song song với nhau khi và chỉ khi 

\(\left\{{}\begin{matrix}m^2=1\\m+1\ne3-m\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}m=\pm1\\m\ne1\end{matrix}\right.\)

Vậy với m = - 1 thì hai đường .thẳng đã cho song song với nhau.

Lời giải:

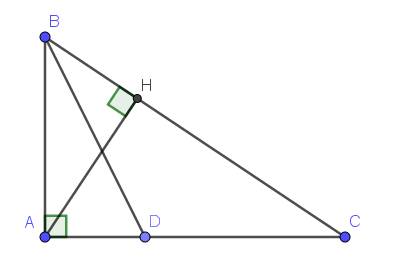
a. Xét tam giác $ABC$ và $HBA$ có:

$\widehat{B}$ chung

$\widehat{BAC}=\widehat{BHA}=90^0$

$\Rightarrow \triangle ABC\sim \triangle HBA$ (g.g)

b.

$BC=\sqrt{AB^2+AC^2}=\sqrt{15^2+20^2}=25$ (cm) - định lý Pitago

$AH=2S_{ABC}:BC=AB.AC:BC=15.20:25=12$ (cm)

$BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=9$ (cm) - định lý Pitago

c.

Theo tính chất đường phân giác:

$\frac{DA}{DC}=\frac{AB}{BC}=\frac{15}{25}=\frac{3}{5}$

$DA+DC=AC=20$

$\Rightarrow DA=20:(3+5).3=7,5$ (cm)

$DC=AC-DA=20-7,5=12,5$ (cm)

Hình vẽ:

Đk: \(-1< x< 1\)

Ta có \(2\sqrt{2022\left(1-x^2\right)}\le2023-x^2\) 

Nếu \(0\le x< 1\) thì \(x\left(x+2021\right)\ge0\) 

\(\Leftrightarrow x^2+2021x\ge0\)

\(\Leftrightarrow2023-x^2\le2021x+2023\)

\(\Rightarrow\) \(2\sqrt{2022\left(1-x^2\right)}\le2023-x^2\le2021x+2023\)

\(\Leftrightarrow2\sqrt{2022}\le\dfrac{2021x+2023}{\sqrt{1-x^2}}\)

Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}2022=1-x^2\\x=0\end{matrix}\right.\), vô lý.

Vậy nếu \(0\le x< 1\) thì BĐT đúng.

Xét \(-1< x< 0\) thì đặt \(x=-t\left(0< t< 1\right)\). 

BĐT cần chứng minh \(\Leftrightarrow\dfrac{2023-2021t}{\sqrt{1-t^2}}\ge2\sqrt{2022}\)

Ta có \(2023-2021t\) 

\(=2022-2022t+1+t\)

\(=2022\left(1-t\right)+\left(1+t\right)\)

\(\ge2\sqrt{2022\left(1-t\right)\left(1+t\right)}\)

\(=2\sqrt{2022\left(1-t^2\right)}\)

\(\Leftrightarrow\dfrac{2023-2021t}{\sqrt{1-t^2}}\ge2\sqrt{2022}\)

Dấu "=" xảy ra \(\Leftrightarrow2022-2022t=1+t\) \(\Leftrightarrow t=\dfrac{2021}{2023}\) \(\Leftrightarrow x=-\dfrac{2021}{2023}\)

Vậy ta có đpcm. Dấu "=" xảy ra \(\Leftrightarrow x=-\dfrac{2021}{2023}\)

Trường hợp \(x\) = - \(\dfrac{2020}{2021}\) thì sao em nhỉ?

pt đã cho \(\Leftrightarrow\left(x-y\right)\left(x+3y\right)=2x+6y-x+y\)

\(\Leftrightarrow\left(x-y\right)\left(x+3y\right)=2\left(x+3y\right)-\left(x-y\right)\)

Đặt \(\left\{{}\begin{matrix}x-y=a\\x+3y=b\end{matrix}\right.\) với \(a,b\inℤ\) và \(b\ge4\)

pt thành \(ab=2a-b\)

\(\Leftrightarrow ab-2a+b-2=-2\)

\(\Leftrightarrow\left(a+1\right)\left(b-2\right)=-2\) (*)

 Vì \(b\ge4\Leftrightarrow b-2\ge2\). Do đó (*) \(\Rightarrow\) \(b-2=2\) hay \(b=4\), nghĩa là dấu "=" phải xảy ra \(\Leftrightarrow x=y=1\). Thử lại, ta thấy không thỏa mãn.

 Vậy pt đã cho không có nghiệm nguyên dương.

a) ĐK: \(\left\{{}\begin{matrix}x-2\ne0\\x+2\ne0\\4-x^2\ne0\\x^2-4\ne0\end{matrix}\right.\Leftrightarrow x\ne\pm2\)

\(A=\left(\dfrac{x+2}{x-2}-\dfrac{1}{x+2}-\dfrac{x-4}{4-x^2}\right):\dfrac{1}{x^2-4}\)

\(A=\left[\dfrac{x+2}{x-2}-\dfrac{1}{x+2}+\dfrac{x-4}{\left(x+2\right)\left(x-2\right)}\right]\cdot\left(x^2-4\right)\)

\(A=\left[\dfrac{\left(x+2\right)^2}{\left(x+2\right)\left(x-2\right)}-\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-4}{\left(x+2\right)\left(x-2\right)}\right]\cdot\left(x^2-4\right)\)

\(A=\dfrac{x^2+4x+4-x+2+x-4}{\left(x+2\right)\left(x-2\right)}\cdot\left(x+2\right)\left(x-2\right)\)

\(A=x^2+4x+2\)

b) \(A=14\)

\(\Leftrightarrow x^2+4x+2=14\)

\(\Leftrightarrow x^2+4x-12=0\)

\(\Leftrightarrow x^2-2x+6x-12=0\)

\(\Leftrightarrow x\left(x-2\right)+6\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x+6\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(ktm\right)\\x=-6\left(tm\right)\end{matrix}\right.\)