Cho 30 điểm phân biệt trong đó có a điểm thẳng hàng cứ qua 2 điểm ta vẽ được 1 đường thẳng. Tìm a, biết số đường thẳng tạo thành là 421 đường thẳng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,3a+2b⋮17\\ =>17a+3a+2b⋮17\\ =>20a+2b⋮17\\ =>2\left(10a+b\right)⋮17\\ =>10a+b⋮17\)
\(b,xy+x-y=4\\ x\left(y+1\right)-y=4\\ x\left(y+1\right)-y-1=4-1\\ x\left(y+1\right)-\left(y+1\right)=3\\ \left(x-1\right)\left(y+1\right)=3\\ Ư\left(3\right)=\left\{1;-1;3;-3\right\}\\ Th1:x-1=1=>x=2;y+1=3=>y=2\\ Th2:x-1=3=>x=4;y+1=1=>y=0\\ Th3:x-1=-1=>x=0;y+1=-3=>y=-4\\ Th4:x-1=-3=>x=-2;y+1=-1=>y=2\)

! là giai thừa em nhé.
3! = 1.2.3
4! = 1.2.3.4
n! = 1.2.3.4.5...n

Mình trả lời rồi mà không được, bạn vào trang cá nhân của mình xem nhé!

Olm chào em, ý em là như nào em nhỉ?
Em vẫn thoát ra và đang sử dụng diễn đàn Olm được đây thôi.
Không cô ơi , em bị vào đó rồi em bấm vào chỗ tên bẫm vào câu hỏi rồi em hỏi chứ ko ra đc ạ cách ra ngoài là j ạ ?

Số số hạng là \(\dfrac{2x-1-1}{2}+1=\dfrac{2x-2}{2}+1=x\left(số\right)\)
Tổng của dãy số là \(\dfrac{x\left(2x-1+1\right)}{2}=x^2\)
Do đó, ta có: \(x^2=225\)
=>\(\left[{}\begin{matrix}x=15\left(nhận\right)\\x=-15\left(loại\right)\end{matrix}\right.\)
Vậy: x=15

Bài 6:
\(A=ax+bx+3ay+3by\)
\(=x\left(a+b\right)+3y\left(a+b\right)\)
\(=\left(a+b\right)\left(x+3y\right)=5\cdot7=35\)
Bài 7:
a: \(\left(2x-4\right)^2>=0\forall x\)
\(\left(3y-9\right)^4>=0\forall y\)
Do đó: \(\left(2x-4\right)^2+\left(3y-9\right)^4>=0\forall x,y\)
mà \(\left(2x-4\right)^2+\left(3y-9\right)^4< =0\forall x,y\)
nên \(\left\{{}\begin{matrix}2x-4=0\\3y-9=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)
b; (\(x^3\) - 1)(\(x^3\) - 10)(\(x^3\) - 30)(\(x^3\) - 70) < 0
Đặt \(x^3\) = t
Khi đó: T = (t - 1)(t - 10)(t - 30)(t - 70) < 0
Lập bảng xét dấu ta có:
| t | 1 10 30 70 |
| t - 1 | - 0 + + + + |
| t - 10 | - - 0 + + + |
| t - 30 | - - - 0 + + |
| t - 70 | - - - - 0 + |
| T = (t - 1).(t - 10).(t - 30).(t - 70) | + 0 - 0 + 0 - 0 + |
Theo bảng trên ta có:
1 < t < 10 hoặc 30 < t < 70
⇒ 1 < \(x^3\) - 1 < 10 ⇒ 2 < \(x^3\) < 11
Vì \(x\) nguyên nên \(x\)3 = 8 ⇒ \(x^3\) = 23 ⇒ \(x=2\)
30 < t < 70
30 < \(x^3\) - 1 < 70
31 < \(x^3\) < 71
Vì \(x\) nguyên nên \(x^3\) = 64
⇒ \(x^3\) = 43 ⇒ \(x\) = 4
Vậy \(x\) \(\in\) {2; 4}

\(0,36\cdot4+36\%+2+2\cdot4\cdot0,18\)
\(=0,36\cdot4+0,18\cdot8+0,36+2\)
\(=0,36\cdot5+0,36\cdot4+2\)
\(=0,36\cdot9+2=2+3,24=5,24\)

Giải:
Gọi số tự nhiên nhỏ nhất cần tìm là \(x\); \(x\in\) N thì theo bài ra ta có:
Số thứ hai là: \(x\) + 1
Số thứ ba là: \(x+1+1\) = \(x\) + 2
Theo bài ra ta có: \(x\) + \(x\) + 1 + \(x\) + 2 = 183
(\(x\) + \(x\) + \(x\)) + (1 + 2) = 183
3\(x\) + 3 = 183
3\(x\) = 183 - 3
3\(x\) = 180
\(x\) = 180 : 3
\(x\) = 60
Vậy số tự nhiên nhỏ nhất thỏa mãn đề bài là: 60
Trung bình cộng của ba số là : 183:3=61
Vì trung bình cộng của ba số là số thứ hai.
Số nhỏ nhất là:61-1=60
Đáp số:60.

\(4,6.\left(168-120\right)+\left(2,1+2,5\right).\left(15+35\right)+\left(11,9-2,7\right)\)
\(=4,6.48+4,6.50+9,2\)
\(=4,6.48+4,6.50+4,6.2\)
\(=4,6.\left(48+50+2\right)\)
\(=4,6.100\)
\(=460\)
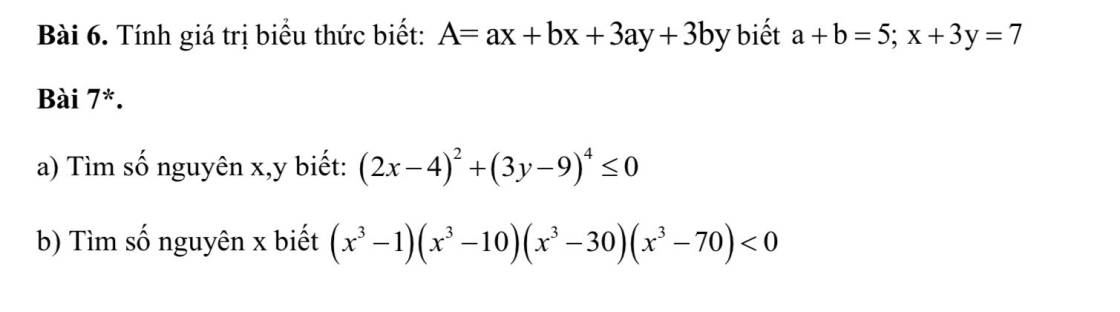
Số điểm còn lại là 30-a(điểm)
TH1: Vẽ 1 đường thẳng đi qua 2 điểm trong a điểm thẳng hàng
=>Có \(C^2_a\left(đường\right)\)
TH2: Chọn 1 điểm trong a điểm thẳng hàng, chọn 1 điểm trong 30-a điểm còn lại
=>Có \(a\left(30-a\right)\left(đường\right)\)
TH3: Chọn 2 điểm trong 30-a điểm còn lại
=>Có \(C^2_{30-a}\left(đường\right)\)
Theo đề, ta có:
\(C^2_a+a\left(30-a\right)+C^2_{30-a}=421\)
=>\(\dfrac{a!}{\left(a-2\right)!\cdot2!}+a\left(30-a\right)+\dfrac{\left(30-a\right)!}{\left(30-a-2\right)!\cdot2!}=421\)
=>\(\dfrac{a\left(a-1\right)}{2}+a\left(30-a\right)+\dfrac{\left(a-29\right)\left(a-30\right)}{2}=421\)
=>\(a\left(a-1\right)+2a\left(30-a\right)+\left(a-29\right)\left(a-30\right)=842\)
=>\(a^2-a+60a-2a^2+a^2-59a+870=842\)
=>870=842(loại)
=>Không có giá trị nào của a thỏa mãn