a: Xét ΔAMB và ΔNMC có

MA=MN

góc AMB=góc NMC

MB=MC

Do đó: ΔAMB=ΔNMC

b: Xét ΔBAI có

BH vừa là đường cao, vừa là trung tuyến

nên ΔBAI cân tại B

=>BA=BI=CN
Đúng thì tick cho mk nha

a:

Sửa đề: \(N\left(x\right)=3x^3-7x^2-x+\dfrac{3}{2}\)

M(x)+N(x)

\(=3x^3-7x^2+\dfrac{4}{5}x-\dfrac{1}{5}+3x^3-7x^2-x+\dfrac{3}{2}\)

\(=6x^3-14x^2-\dfrac{1}{5}x+\dfrac{13}{10}\)

b: H(x)=M(x)-N(x)

\(=3x^3-7x^2+\dfrac{4}{5}x-\dfrac{1}{5}-3x^3+7x^2+x-\dfrac{3}{2}\)

\(=\dfrac{9}{5}x-\dfrac{17}{10}\)

c: Đặt H(x)=0

=>\(\dfrac{9}{5}x-\dfrac{17}{10}=0\)

=>\(\dfrac{9}{5}x=\dfrac{17}{10}\)

=>\(x=\dfrac{17}{10}:\dfrac{9}{5}=\dfrac{17}{10}\cdot\dfrac{5}{9}=\dfrac{17}{18}\)

d: \(P\left(-1\right)=\left(-1\right)^3-3\cdot\left(-1\right)^2+3\cdot\left(-1\right)-1+2\cdot\left(-1\right)^3+\left(-1\right)^2-\left(-1\right)+5\)

\(=-1-3-3-1-2+1+1+5\)

=-3<0

=>x=-1 không là nghiệm của P(x)

\(P\left(x\right)=x^3-3x^2+3x-1+2x^3+x^2-x+5\)

\(=\left(x^3+2x^3\right)+\left(-3x^2+x^2\right)+\left(3x-x\right)+\left(-1+5\right)\)

\(=3x^3-2x^2+2x+4\)

1: Xét ΔMAC và ΔMEB có

MA=ME

\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)

MC=MB

Do đó: ΔMAC=ΔMEB

=>AC=BE

ΔMAC=ΔMEB

=>\(\widehat{MAC}=\widehat{MEB}\)

=>AC//EB

b: Xét ΔIAM và ΔKEM có

IA=KE

\(\widehat{IAM}=\widehat{KEM}\)

AM=ME

Do đó: ΔIAM=ΔKEM

=>\(\widehat{IMA}=\widehat{KME}\)

mà \(\widehat{IMA}+\widehat{IME}=180^0\)(hai góc kề bù)

nên \(\widehat{KME}+\widehat{IME}=180^0\)

=>I,M,K thẳng hàng

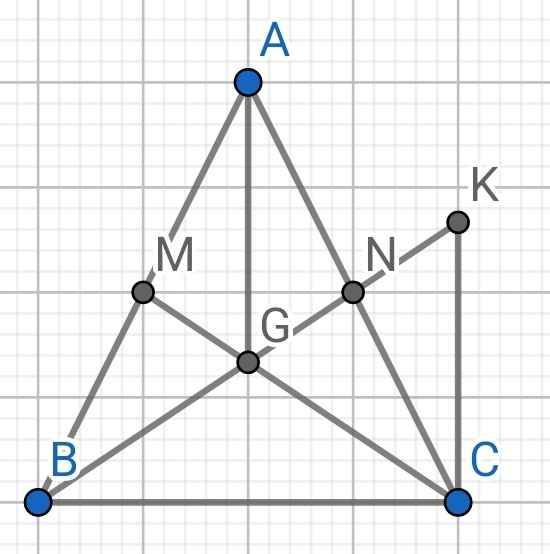
a) Do ∆ABC cân tại A (gt)

⇒ AB = AC (1)

Do M là trung điểm của AB (gt)

⇒ AM = BM = AB : 2 (2)

Do N là trung điểm của AC (gt)

⇒ AN = CN = AC : 2 (3)

Từ (1), (2) và (3) ⇒ AM = AN

b) Xét ∆AGN và ∆CKN có:

AN = CN (cmt)

∠ANG = ∠CNK (đối đỉnh)

GN = NK (gt)

⇒ ∆AGN = ∆CKN (c-g-c)

⇒ ∠AGN = ∠CKN (hai góc tương ứng)

Mà ∠AGN và ∠CKN là hai góc so le trong

⇒ AG // CK

c) Do NG = NK (gt)

⇒ N là trung điểm của GK

⇒ GK = 2GN (4)

Do M là trung điểm của AB (gt)

N là trung điểm của AC (gt)

⇒ BN và CM là hai đường trung tuyến của ∆ABC

Mà BN cắt CM tại G (gt)

⇒ G là trọng tâm của ∆ABC

⇒ BG = 2GN (5)

Từ (4) và (5) ⇒ BG = GK

d) Do ∆AGN = ∆CKN (cmt)

⇒ AG = CK (hai cạnh tương ứng)

Do BG = 2GN (cmt)

GK = 2GN (cmt)

⇒ BG + GK = 4GN

⇒ BK = 4GN

∆BCK có:

BC + CK > BK (bất đẳng thức tam giác)

⇒ BC + CK > 4GN

Mà CK = AG (cmt)

⇒ BC + AG > 4GN

Chọn B

Vì 5\(x^4\) là hạng tử có chứa bậc cao nhất của đa thức nên bậc của hạng tử này là bậc của đa thức

bậc của hạng tử này là 4

Vậy bậc của đa thức là 4

Chọn B.4

\(\dfrac{x}{5}=2\)

\(x=5.2\)

\(x=10\)

\(\dfrac{x}{5}=2\)

⇒x=2.5=10

Vậy x=10

a: Xét ΔMNI có MN<MI<NI

mà \(\widehat{MIN};\widehat{MNI};\widehat{NMI}\) lần lượt là góc đối diện của các cạnh MN,MI,NI

nên \(\widehat{MIN}< \widehat{MNI}< \widehat{NMI}\)

b: Xét ΔNID có

IM,DK là các đường trung tuyến

IM cắt DK tại E

Do đó: E là trọng tâm của ΔNID

=>\(IE=\dfrac{2}{3}IM=\dfrac{2}{3}\cdot16=\dfrac{32}{3}\left(cm\right)\)

IE+EM=IM

=>\(EM+\dfrac{32}{3}=16\)

=>\(EM=\dfrac{16}{3}\left(cm\right)\)

Đề yêu cầu gì em nhỉ?

Hai lần hiệu của a và b là:

\(2\left(a-b\right)=2a-2b\)

Câu 6:

a: Đặt M(x)=0

=>\(2x-\dfrac{1}{2}=0\)

=>\(2x=\dfrac{1}{2}\)

=>\(x=\dfrac{1}{4}\)

b: Đặt N(x)=0

=>\(\left(x+5\right)\left(4x^2-1\right)=0\)

=>(x+5)(2x-1)(2x+1)=0

=>\(\left[{}\begin{matrix}x+5=0\\2x-1=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=\dfrac{1}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)

c: Đặt P(x)=0

=>\(9x^3-25x=0\)

=>\(x\cdot\left(9x^2-25\right)=0\)

=>x(3x-5)(3x+5)=0

=>\(\left[{}\begin{matrix}x=0\\3x-5=0\\3x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{5}{3}\\x=-\dfrac{5}{3}\end{matrix}\right.\)

Câu 7:

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

=>HB=HC

ΔAHB=ΔAHC

=>\(\widehat{BAH}=\widehat{CAH}\)

=>AH là phân giác của góc BAC

b: Xét ΔBDE và ΔBHA có

BD=BH

\(\widehat{DBE}=\widehat{HBA}\)(hai góc đối đỉnh)

BE=BA

Do đó: ΔBDE=ΔBHA

=>\(\widehat{BDE}=\widehat{BHA}\)

=>AH//DE
c: Ta có: AH=DE

mà AH<AD(ΔAHD vuông tại H)

nên DE<DA

Xét ΔDAE có DE<DA

mà \(\widehat{DAE};\widehat{DEA}\) lần lượt là góc đối diện của các cạnh DE,DA

nên \(\widehat{DAE}< \widehat{DEA}\)

=>\(\widehat{DAB}< \widehat{BAH}\)

help me