Vì 3311 = 11 . 301 nên 3311 có ước là 11 và 301. Vậy 3311 là một hợp số.

Ta có: `3311 = 11 .301`

`->` Số `3311` là hợp số.

hợp số bạn nhé

= 81(172+828)

= 81. 1000

=81000

\(172x81+828x81\\ =81\left(172+828\right)\\ 81x1000=81000\)

`326 + (153 - x) = 403`

`=> 153 - x = 403 - 326`

`=> 153-x=77`

`=> x=153-77`

`=>x=76`

Vậy: `x=76`

326 + (153 - x) = 403

=> 153 - x = 403 - 326

=> 153-x=77

=> x=153-77

=>x=76

Vậy: x=76

`x` \(\in B\left(11\right),10< x< 40\)

\(\Rightarrow B\left(11\right)=\left\{0;11;22;33;44;...\right\}\)

Mà \(10< x< 40\)

\(\Rightarrow x\in\left\{11;22;33\right\}\)

x = 11;22;33

Số học sinh giỏi học kì 1 chiếm số phần là: 

`2 : (7+2) = 2/9` (học sinh cả lớp) 

Số học sinh giỏi học kì 2 chiếm số phần là: 

`2 : (2+3) = 2/5` (học sinh cả lớp) 

8 bạn ứng với số phần của lớp là: 

`2/5 - 2/9 = 8/45` (học sinh cả lớp)

Lớp 7A có số học sinh là: 

`8 : 45= 45` (học sinh)

Số học sinh giỏi kì 1 là: 

`45 xx 2/9 = 10 ` (học sinh)

Đáp số: ...

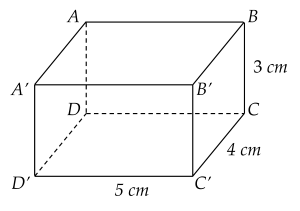
a) Thể tích hình hộp chữ nhật là: 

3 xx 4 xx 5 = 60 (cm^3) 

b) Thể tích lăng trụ đứng tam giác là: 

3 xx 4 : 2 xx 5 = 30 (cm^3)

S xung quanh lăng trụ đứng tam giác là: 

(3+4+5) xx 5 = 60 (cm^2)

Đáp số: ...

`x + 5/6 = 4/3 `

`=> x = 4/3 - 5/6`

`=> x = 8/6 - 5/6`

`=> x = 3/6`

`=> x = 1/2`

Vậy ...

`x : 2^4 = 8^3`

`=> x : 2^4 = 2^9`

`=> x = 2^9 . 2^4`

`=> x = 2^13`

Vậy ...

`13/4 : (5/52 - x ) = 1/4`

`=> 5/52 - x = 13/4 : 1/4`

`=> 5/52 - x = 13`

`=> x = 5/52 - 13`

`=> x = -671/52`

Vậy ...

`a) x+5/6=4/3`

`x=4/3- 5/6`

`x=1/2`

`b) x: 2^4= 8^3`

`x:2^4= 2^9`

`x=2^9. 2^4`

`x=2^13`

`c) 13/4.(5/52 -  x)=1/4`

`(5/52-x)=13/4: 1/4`

`5/52 -x= 13`

`x=5/52- 13`

`x= -671/52`

`a) 5/9 - (1/3)^2= 5/9- 1/9= 4/9`

`b) 1/5. -3/2 + -17/2. 1/5= 1/5. (-3/2+-17/2)= 1/5.(-10)= -2`

`c) 1+ (-2/5 + 11/13) - (3/5- 2/13)= 1+ -2/5 + 11/13 + -3/5 + 2/13= 1+ (-2/5+ -3/5) +  (11/13+2/13) =1+ (-1)+1=1`

`a, 36 + 75 + 64 + 25 + 99`

`= (36 + 64) + (75 + 25) + 99`

`= 100 + 100 + 99`

`= 200 + 99`

`= 299`

`b, 2024^0 + 3 * [5^2 * 10 - (23 - 13)^2]`

`= 1 + 3*[5^2 * 10 - 10^2]`

`= 1 + 3*[25 * 10 - 100]`

`= 1 + 3*[250 - 100]`

`= 1 + 3* 150`

`= 1 + 450`

`= 451`

\(c,4^2\cdot65+35\cdot4^2-1500\)

`= 4^2 * (65 + 35) - 1500`

`= 16 * 100 - 1500`

`= 1600 - 1500`

`= 100`

a; 36 + 75  + 64 + 25+ 99

= (36 + 64) + (75 + 25) + 99

= 100 + 100 + 99

= 200 + 99

= 299

b;2024⁰ + 3.[5².10 - (23 - 13)²]

  1 + 3.[25.10 - 10²] 

= 1 + 3.[250 - 100]

= 1 +3.150

= 1 +450

= 451 

c; 4².65 + 35.4² - 1500

= 4².(65 + 35) - 1500

= 4².100 - 15.100

= 100.(4² - 15)

= 100.(16 - 15)

= 100.1

= 100