1/1x3+1/3x5+1/5x7+...+1/2007x2009+1/2009x2011
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Độ dài đường chéo thứ nhất là:
411:3x2=274(m)
Độ dài đường chéo thứ hai là:
274:2=137(m)
Diện tích hình thoi là: \(274\cdot\dfrac{137}{2}=18769\left(m^2\right)\)
Tỉ số đường chéo thứ nhất và đường chéo thứ hai là: \(\dfrac{2}{1}\)
Tổng số phần bằng nhau là:
\(2+1=3\) (phần)
Đường chéo thứ nhất là:
\(411:3\cdot2=274\left(m\right)\)
Đường chéo thứ hai là:
\(411-274=137\left(m\right)\)
Diện tích hình thoi là:
\(\dfrac{274\cdot137}{2}=18769\left(m^2\right)\)
Đáp số: \(18769m^2\)

Nếu \(f\left(x\right)=0\) có nghiệm trên \(\left[-1;1\right]\Rightarrow\min\limits_{\left[-1;1\right]}\left[f\left(x\right)\right]^2=0\) ko thỏa mãn yêu cầu
\(\Rightarrow f\left(x\right)=0\) vô nghiệm trên \(\left[-1;1\right]\)
Khi đó
\(f'\left(x\right)=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow f'\left(x\right)\le0;\forall x\in\left[-1;1\right]\)
Xét hàm \(y=\left[f\left(x\right)\right]^2\) trên \(\left[-1;1\right]\)
\(y=\left[f\left(x\right)\right]^2\Rightarrow y'=2f'\left(x\right).f\left(x\right)\)
Do \(f'\left(x\right)\le0\) và \(f\left(x\right)=0\) vô nghiệm (nên ko đổi dấu) trên \(\left[-1;1\right]\) nên:
TH1: \(f\left(x\right)>0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1>-m\)
\(\Rightarrow-m< \min\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=-1\)
\(\Rightarrow m>1\)
Khi đó \(f'\left(x\right).f\left(x\right)\le0\Rightarrow y=\left[f\left(x\right)\right]^2\) nghịch biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(1\right)=\left(1-3+m+1\right)^2=\left(m-1\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=0< 1\left(loại\right)\\m=2\end{matrix}\right.\)
TH2: \(f\left(x\right)< 0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1< -m\)
\(\Rightarrow-m>\max\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=3\)
\(\Rightarrow m< -3\)
Khi đó \(f'\left(x\right).f\left(x\right)\ge0\Rightarrow y=\left[f\left(x\right)\right]^2\) đồng biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(-1\right)=\left(-1+3+m+1\right)^2=\left(m+3\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=-2>-3\left(loại\right)\\m=-4\end{matrix}\right.\)
Vậy \(m=2;m=-4\) (C đúng)
\(\text{Viết các số 9673,3547:}\)\(\overline{abcde}\)\(\text{ dưới dạng tổng các luỹ thừa của 10.}\)

`9673=9000+600+70+3`
`=9*10^3+6*10^2+7*10+3`
`3547=3000+500+40+7`
`=3*10^3+5*10^2+4*10+7`
\(\overline{abcde}\)`=a*10000+b*1000+c*100+d*10+e`
`=a*10^4+b*10^3+c*10^2+d*10+e`
\(9673=9\cdot10^3+6\cdot10^2+7\cdot10^1+3\cdot10^0\\ 3547=3\cdot10^3+5\cdot10^2+4\cdot10^1+7\cdot10^0\\ abcde=a\cdot10^4+b\cdot10^3+c\cdot10^2+d\cdot10^1+e\cdot10^0\)

\(\dfrac{2}{5\times7}+\dfrac{2}{7\times9}+...+\dfrac{2}{13\times15}\)
\(=\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{13}-\dfrac{1}{15}\)
\(=\dfrac{1}{5}-\dfrac{1}{15}=\dfrac{2}{15}\)
`2/(5 xx 7)+2/(7 xx 9) + ... + 2/(13 xx 15)`
`=1/5-1/7+1/7-1/9+...+1/13-1/15`
`=1/5+(1/7-1/7)+(1/9-1/9)+...+(1/13-1/13)-1/15`
`=1/5-1/15`
`=3/15-1/15`
`=2/15`

Ta có:
\(25^9=\left(5^2\right)^9=5^{18}\)
Vì: \(5^{17}< 5^{18}\) nên \(5^{17}< 25^9\)
Ta có:
\(3^{90}=\left(3^3\right)^{30}=27^{30}\)
\(4^{60}=\left(4^2\right)^{30}=16^{30}\)
Vì: \(27^{30}>16^{30}\) nên \(3^{90}>4^{60}\)
Bài 1:
c: \(18\cdot\left[\left(3^4\cdot29+3^4\cdot6+3^4\cdot34\right)-71\cdot1^{56}\right]-80\)
\(=18\cdot\left[3^4\left(29+6+34\right)-71\right]-80\)
\(=18\cdot\left[81\cdot69-71\right]-80\)
\(=18\cdot5518-80=99244\)
b: \(\left[19+\left(3^5-62\right)\right]\cdot x=10^3\cdot10\)
=>\(\left(243-62+19\right)\cdot x=10000\)
=>\(200x=10000\)
=>x=10000:200=50
Bài 2:
\(25^9=\left(5^2\right)^9=5^{18}>5^{17}\)
\(3^{90}=\left(3^3\right)^{30}=27^{30};4^{60}=\left(4^2\right)^{30}=16^{30}\)
mà 27>16
nên \(3^{90}>4^{60}\)

Chiều cao của hình bình hành là:
\(189:7=27\left(m\right)\)
Diện tích ban đầu là \(47\cdot\dfrac{27}{2}=634,5\left(m^2\right)\)
Sau khi mở rộng, cạnh đáy mới là:
\(47+7=54\left(m\right)\)
Chiều cao hình bình hành sau khi tăng là:
\(189:7=27\left(m\right)\)
Diện tích ban đầu là:
\(47\cdot27=1269\left(m^2\right)\)
Đáp số: \(1269m^2\)

a: \(\left|x+\dfrac{1}{2}\right|>=0\forall x\)
Dấu '=' xảy ra khi \(x+\dfrac{1}{2}=0\)
=>\(x=-\dfrac{1}{2}\)
b: \(\left|x-\dfrac{1}{3}\right|>=0\forall x\)
=>\(\left|x-\dfrac{1}{3}\right|+2>=2\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{1}{3}=0\)
=>\(x=\dfrac{1}{3}\)

\(\left(x-2\right)^2-\left(x+1\right)\left(x-3\right)=-7\\ \Rightarrow x^2-4x+4-\left(x^2-2x-3\right)=-7\\ \Rightarrow x^2-4x+4-x^2+2x+3=-7\\ \Rightarrow-2x+7=-7\\ \Rightarrow-2x=-14\\ \Rightarrow x=-14:\left(-2\right)\\ \Rightarrow x=7\)
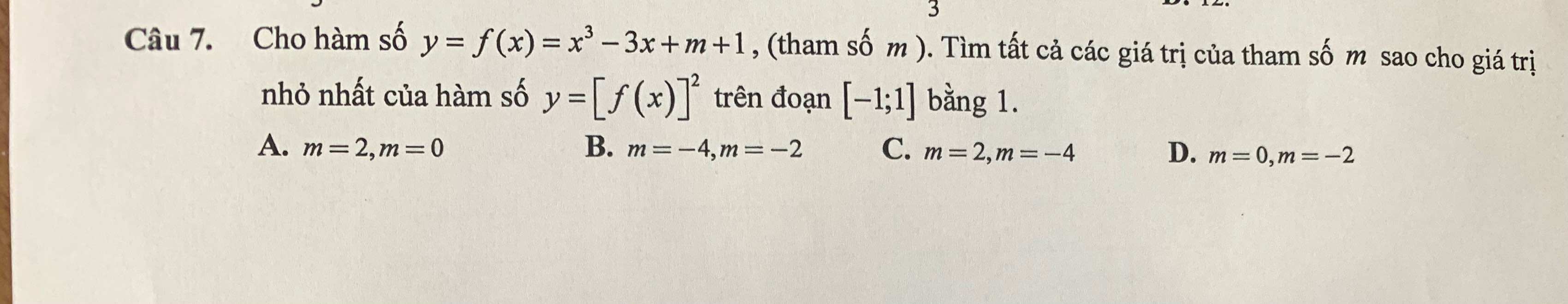

\(\dfrac{1}{1\times3}+\dfrac{1}{3\times5}+\dfrac{1}{5\times7}+...+\dfrac{1}{2007\times2009}+\dfrac{1}{2009\times2011}\\ =\dfrac{1}{2}\times\left(\dfrac{2}{1\times3}+\dfrac{2}{3\times5}+\dfrac{2}{5\times7}+...+\dfrac{2}{2007\times2009}+\dfrac{2}{2009\times2011}\right)\\ =\dfrac{1}{2}\times\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...-\dfrac{1}{2009}+\dfrac{1}{2009}-\dfrac{1}{2011}\right)\\ =\dfrac{1}{2}\times\left(1-\dfrac{1}{2011}\right)\\ =\dfrac{1}{2}\times\dfrac{2010}{2011}\\ =\dfrac{1005}{2011}\)