\(2x^2+2y^2-4xy+2x-2y=1\) Tìm x,y nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để giải phương trình này, ta có thể sử dụng một số phân tích như sau:
1. Trường hợp đặc biệt: Nếu (a = b), thì phương trình trở thành (a^a = a^a), điều này luôn đúng với mọi giá trị của (a).
2. Trường hợp (a = 1) hoặc (b = 1): Nếu một trong hai số là 1, thì phương trình trở thành (1^b = b^1), điều này cũng luôn đúng với mọi giá trị của (b).
3. Trường hợp (a = 2) và (b = 4): Ta thấy rằng (2^4 = 4^2), vậy đây là một giá trị thỏa mãn.
4. Trường hợp (a = 4) và (b = 2): Ta thấy rằng (4^2 = 2^4), vậy đây cũng là một giá trị thỏa mãn.
Vậy, các cặp giá trị thỏa mãn phương trình là ((a, b) = (2, 4)) và ((a, b) = (4, 2)).

a) Thay tọa độ điểm M(1; 4) vào (d), ta có:
(-2m + 1).1 + m - 3 = 4
-2m + 1 + m - 3 = 4
-2m - 2 = 4
-m = 4 + 2
-m = 6
m = -6
b) m = -6
(d): y = 13x - 9
Bảng giá trị:
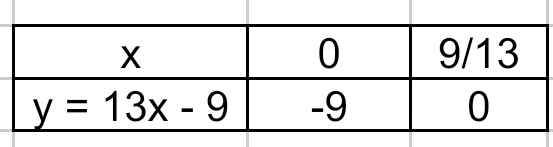
Đồ thị:
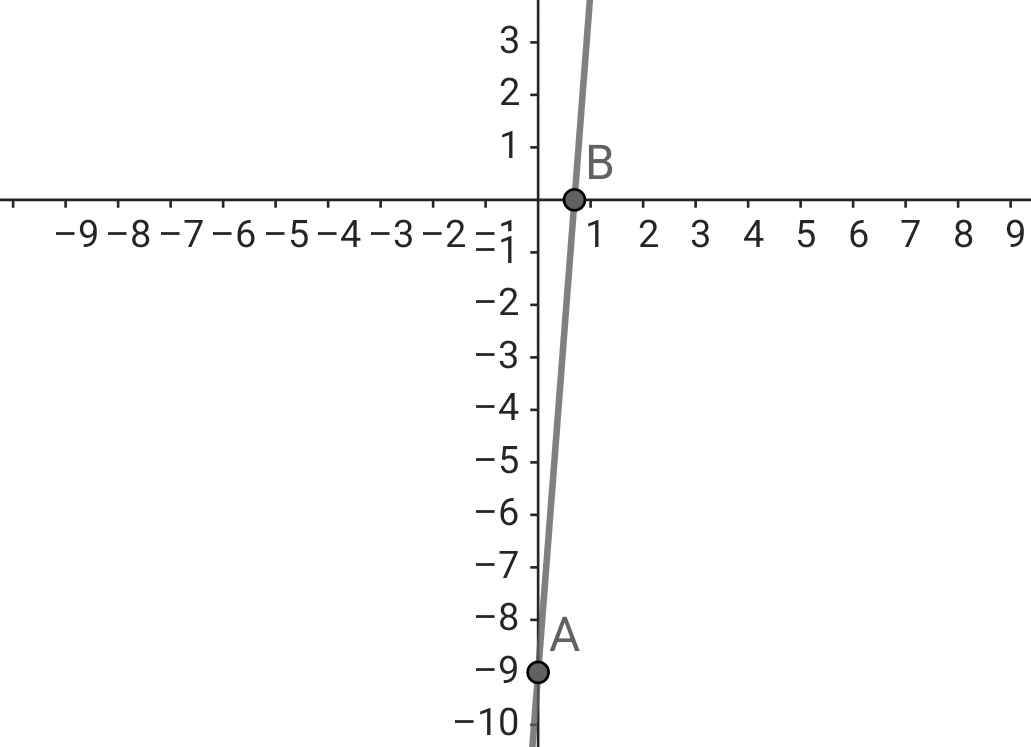
a;
Để d đi qua điểm A(1; 4)
Thì tọa độ điểm A phải thỏa mãn phương trình đường thẳng d
Thay tọa độ điểm A vào phương trình đường thẳng d ta có:
(-2m + 1).\(1\) + m - 3 = 4
-2m + 1 + m - 3 = 4
-m - 2 = 4
m = - 2 - 6
m = - 8

Olm chào em, lần sau em chụp ảnh câu hỏi vào đây để olm dễ check lại em nhé. Cảm ơn em đã tin tưởng và sử dụng olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm.

Nửa chu vi tam giác:
\(\dfrac{\left(10+17+21\right)}{2}=24\left(cm\right)\)
Diện tích tam giác:
\(S=\sqrt{24.\left(24-10\right).\left(24-17\right).\left(24-21\right)}=84\left(cm^2\right)\)
Xét Δ𝐴𝐵𝐶ΔABC có 𝐴𝐵=10AB=10 cm, 𝐴𝐶=17AC=17 cm, 𝐵𝐶=21BC=21 cm.
Gọi 𝐴𝐻AH là đường cao của tam giác.

Vì 𝐵𝐶BC là cạnh lớn nhất của tam giác nên 𝐵^,𝐶^<90∘B,C<90∘, do đó 𝐻H nằm giữa 𝐵B và 𝐶C.
Đặt 𝐻𝐶=𝑥,𝐻𝐵=𝑦HC=x,HB=y, ta có : 𝑥+𝑦=21x+y=21 (1)
Mặt khác 𝐴𝐻2=102−𝑦2,𝐴𝐻2=172−𝑥2AH2=102−y2,AH2=172−x2 nên 𝑥2−𝑦2=172−102=289−100=189x2−y2=172−102=289−100=189 (2)
Từ (1) và (2) suy ra 𝑥+𝑦=21x+y=21, 𝑥−𝑦=9x−y=9.
Do đó 𝑥=15x=15, 𝑦=6y=6.
Ta có 𝐴𝐻2=102−62=64AH2=102−62=64 nên 𝐴𝐻=8AH=8.
Vậy 𝑆𝐴𝐵𝐶=21.82=84SABC=221.8=84 (cm22).

Chiều cao của mỗi hình chóp tứ giác đều là:
30:2=1530:2=15 (m).
Thể tích của lồng đèn quả trám là:
𝑉=2.(13.20.20.15)=4000V=2.(31.20.20.15)=4000 (cm33).


a) Xét hai tam giác vuông: \(\Delta BHK\) và \(\Delta CHI\) có:
\(\widehat{BHK}=\widehat{CHI}\) (đối đỉnh)
\(\Rightarrow\Delta BHK\) ∽ \(\Delta CHI\left(g-g\right)\)
b) Do \(BH\) là tia phân giác của \(\widehat{KBC}\) (gt)
\(\Rightarrow\widehat{KBH}=\widehat{CBH}\)
\(\Rightarrow\widehat{KBH}=\widehat{CBI}\) (1)
Do \(\Delta BHK\) ∽ \(\Delta CHI\left(cmt\right)\)
\(\Rightarrow\widehat{KBH}=\widehat{ICH}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{ICH}=\widehat{CBI}\)
Xét hai tam giác vuông: \(\Delta CIB\) và \(\Delta HIC\) có:
\(\widehat{CBI}=\widehat{ICH}\left(cmt\right)\)
\(\Rightarrow\Delta CIB\) ∽ \(\Delta HIC\left(g-g\right)\)
\(\Rightarrow\dfrac{CI}{IH}=\dfrac{IB}{CI}\)
\(\Rightarrow CI^2=IH.IB\)
c) Do \(CI\perp BH\) tại \(I\) (gt)
\(\Rightarrow BI\perp AC\)
\(\Rightarrow BI\) là đường cao của \(\Delta ABC\)
Lại có:
\(CK\perp KB\left(gt\right)\)
\(\Rightarrow CK\perp AB\)
\(\Rightarrow CK\) là đường cao thứ hai của \(\Delta ABC\)
Mà H là giao điểm của \(BI\) và \(CK\) (gt)
\(\Rightarrow AH\) là đường cao thứ ba của \(\Delta ABC\)
\(\Rightarrow AD\perp BC\)
Xét hai tam giác vuông: \(\Delta BKH\) và \(\Delta BDH\) có:
\(BH\) là cạnh chung
\(\widehat{KBH}=\widehat{DBH}\) (do BH là tia phân giác của \(\widehat{B}\))
\(\Rightarrow\Delta BKH=\Delta BDH\) (cạnh huyền - góc nhọn)
\(\Rightarrow BK=BD\) (hai cạnh tương ứng)
\(\Rightarrow B\) nằm trên đường trung trực của DK (3)
Do \(\Delta BKH=\Delta BDH\left(cmt\right)\)
\(\Rightarrow HK=HD\) (hai cạnh tương ứng)
\(\Rightarrow H\) nằm trên đường trung trực của DK (4)
Từ (3) và (4) \(\Rightarrow BH\) là đường trung trực của DK
\(\Rightarrow\widehat{DKH}+\widehat{BHK}=90^0\)
Mà \(\widehat{BHK}=\widehat{CHI}\) (cmt)
\(\Rightarrow\widehat{DKH}+\widehat{CHI}=90^0\) (*)
\(\Delta ABC\) có:
\(BH\) là đường phân giác (cmt)
\(BH\) cũng là đường cao (cmt)
\(\Rightarrow\Delta ABC\) cân tại B
\(\Rightarrow BH\) là đường trung trực của \(\Delta ABC\)
\(\Rightarrow I\) là trung điểm của AC
\(\Rightarrow KI\) là đường trung tuyến của \(\Delta AKC\)
\(\Delta AKC\) vuông tại K có KI là đường trung tuyến ứng với cạnh huyền AC
\(\Rightarrow KI=IC=IA=\dfrac{AC}{2}\)
\(\Rightarrow\Delta IKC\) cân tại \(I\)
\(\Rightarrow\widehat{IKC}=\widehat{ICK}\)
\(\Rightarrow\widehat{IKH}=\widehat{ICH}\)
Mà \(\widehat{ICH}+\widehat{CHI}=90^0\)
\(\Rightarrow\widehat{IKH}+\widehat{CHI}=90^0\) (**)
Từ (*) và (**) \(\Rightarrow\widehat{IKH}=\widehat{DKH}\)
\(\Rightarrow KH\) là tia phân giác của \(\widehat{IKD}\)
Hay \(KC\) là tia phân giác của \(\widehat{IKD}\)
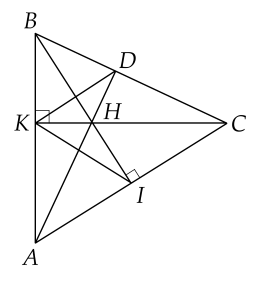
a) Vì tam giác 𝐾𝐵𝐶KBC vuông tại 𝐾K suy ra 𝐾𝐵𝐻^=90∘KBH=90∘
Vì 𝐶𝐼⊥𝐵𝐼CI⊥BI (gt) suy ra 𝐶𝑙𝐻^=90∘ClH=90∘
Xét △𝐾𝐵𝐻△KBH và △𝐶𝐻𝐼△CHI có:
𝐾𝐵𝐻^=𝐶𝐼𝐻^=90∘KBH=CIH=90∘;
𝐵𝐻𝐾^=𝐶𝐻𝐼^BHK=CHI (đối đỉnh)
Suy ra Δ𝐵𝐻𝐾∽Δ𝐶𝐻𝐼ΔBHK∽ΔCHI (g.g)
b) Ta có Δ𝐵𝐻𝐾∽Δ𝐶𝐻𝐼ΔBHK∽ΔCHI suy ra 𝐻𝐵𝐾^=𝐻𝐶𝐼^HBK=HCI (hai góc tương ứng)
Mà 𝐵𝐻BH là tia phân giác của 𝐴𝐵𝐶^ABC nên 𝐻𝐵𝐾^=𝐻𝐵𝐶^HBK=HBC.
Do đó 𝐻𝐵𝐶^=𝐻𝐶𝐼^HBC=HCI.
Xét △𝐶𝐼𝐵△CIB và △𝐻𝐼𝐶△HIC có:
𝐶𝐼𝐵^CIB chung;
𝐼𝐵𝐶^=𝐻𝐶𝐼^IBC=HCI (cmt)
Vậy Δ𝐶𝐼𝐵≈Δ𝐻𝐼𝐶ΔCIB≈ΔHIC (g.g) suy ra 𝐶𝐼𝐻𝐼=𝐼𝐵𝐼𝐶HICI=ICIB
Hay 𝐶𝐼2=𝐻𝐼.𝐼𝐵CI2=HI.IB
c) Xét △𝐴𝐵𝐶△ABC có 𝐵𝐼⊥𝐴𝐶BI⊥AC; 𝐶𝐾⊥𝐴𝐵CK⊥AB; 𝐵𝐼∩𝐶𝐾={𝐻}BI∩CK={H}
Nên 𝐻H là trực tâm △𝐴𝐵𝐶△ABC suy ra 𝐴𝐻⊥𝐵𝐶AH⊥BC tại 𝐷D.
Từ đó ta có △𝐵𝐾𝐶∽△𝐻𝐷𝐶△BKC∽△HDC (g.g) nên 𝐶𝐵𝐶𝐻=𝐶𝐾𝐶𝐷CHCB=CDCK
Suy ra 𝐶𝐵𝐶𝐾=𝐶𝐻𝐶𝐷CKCB=CDCH nên △𝐵𝐻𝐶∽△𝐾𝐷𝐶△BHC∽△KDC (c.g.c)
Khi đó 𝐻𝐵𝐶^=𝐷𝐾𝐶^HBC=DKC (hai góc tương ứng)
Chứng minh tương tự 𝐻𝐴𝐶^=𝐼𝐾𝐶^HAC=IKC
Mà 𝐻𝐴𝐶^=𝐻𝐵𝐶^HAC=HBC (cùng phụ 𝐴𝐶𝐵^ACB )
Suy ra 𝐷𝐾𝐶^=𝐼𝐾𝐶^ DKC=IKC.
Vậy 𝐾𝐶KC là tia phân giác của 𝐼𝐾𝐷^IKD.

a) Xét △ABC vuông tại A nên: AB2 + AC2 = BC2 (Định lí Pythagore)
suy ra BC = \(\sqrt{AB^2+AC^2}\)
= \(\sqrt{6^2+8^2}\)
= 10
Vậy BC = 10
a: Sửa đề: AB=6
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(\)\(BC^2=6^2+8^2=100=10^2\)
=>BC=10
b: Sửa đề: tính BD,CD
Xét ΔABC có AD là phân giác
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
=>\(\dfrac{DB}{6}=\dfrac{DC}{8}\)
=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)
mà DB+DC=BC=10
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{10}{7}\)
=>\(DB=3\cdot\dfrac{10}{7}=\dfrac{30}{7};DC=4\cdot\dfrac{10}{7}=\dfrac{40}{7}\)
Lời giải:
Với $x,y$ nguyên thì $2x^2+2y^2-4xy+2x-2y$ là 1 số chẵn. Mà $1$ là số lẻ nên không tồn tại $x,y$ nguyên thỏa mãn đề bài.