Số phần quả bóng còn lại so với tổng số bóng ban đầu là:

\(1-\dfrac{1}{7}-\dfrac{1}{5}=1-\dfrac{12}{35}=\dfrac{23}{35}\)

\(\left(x-1\right)+\left(x-2\right)+...+\left(x-20\right)=150\\ x-1+x-2+...+x-20=150\\ \left(x+x+...+x\right)-\left(1+2+...+20\right)\\ 20\cdot x-\left[\left(20-1\right):1+1\right]\cdot\left(20+1\right):2=150\\ 20\cdot x-20\cdot21:2=150\\ 20\cdot x-210=150\\ 20\cdot x=150+210\\ 20\cdot x=360\\ x=360:20\\ x=18\)

Diện tích tam giác ABC là:

\(S_{ABC}=\dfrac{1}{2}ab\cdot sinC=\dfrac{1}{2}\cdot7\cdot23\cdot sin130^o=61,7\) (đvdt) 

Thank you mngười nhìu ạ

Bài 14:

Số bao đường ở mỗi kho ban đầu là:

168:3=56(bao)

Số bao đường ở mỗi kho sau đó là:

56+16=72(bao)

Số bao đường đã bán hết là:

72x2=144(bao)

a: Ta có: \(\widehat{xOy}=\widehat{mOn}\)(hai góc đối đỉnh)

mà \(\widehat{xOy}=50^0\)

nên \(\widehat{mOn}=50^0\)

Ta có: \(\widehat{xOy}+\widehat{mOy}=180^0\)(hai góc kề bù)

=>\(\widehat{mOy}+50^0=180^0\)

=>\(\widehat{mOy}=130^0\)

Ta có: \(\widehat{xOn}=\widehat{mOy}\)(hai góc đối đỉnh)

mà \(\widehat{mOy}=130^0\)

nên \(\widehat{xOn}=130^0\)

b: Oa là phân giác của góc xOy

=>\(\widehat{yOa}=\dfrac{\widehat{xOy}}{2}=25^0\)

Ta có: Ob là phân giác của góc yOm

=>\(\widehat{yOb}=\dfrac{\widehat{yOm}}{2}=65^0\)

Ta có: \(\widehat{aOb}=\widehat{aOy}+\widehat{bOy}=25^0+65^0=90^0\)

Ta có:

+) Vì \(\overline{2abb}⋮\) \(2\) và \(5\)nên:

\(b=0\)

+) Vì \(\overline{2abb}⋮3\) nên:

\(2+a+b+b=2+a+0+0=a+2⋮3\)

\(\Rightarrow\left(a+2\right)\in\left\{3,6,9\right\}\) (vì \(1\le a\le9\))

\(\Rightarrow a\in\left\{1,4,7\right\}\)

Vậy...

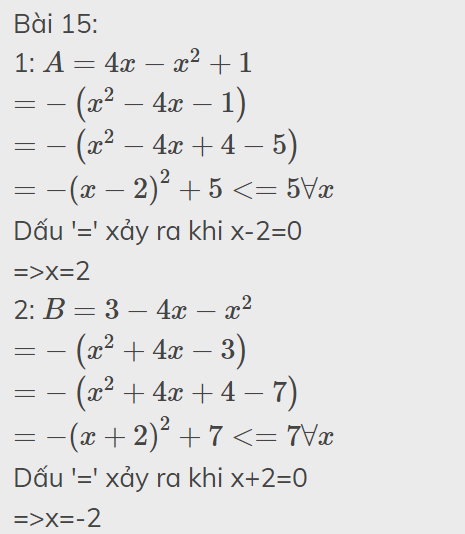
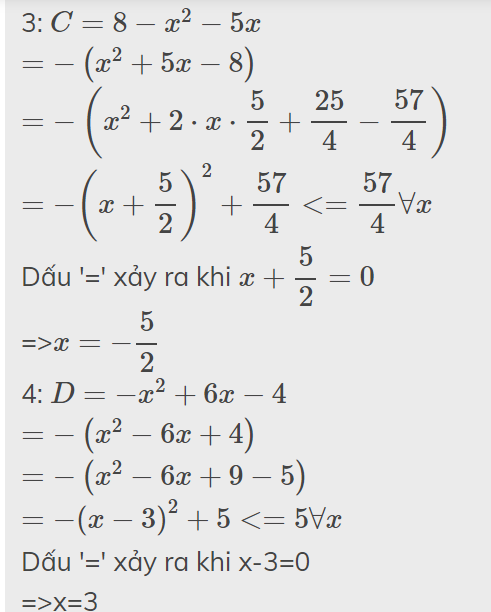
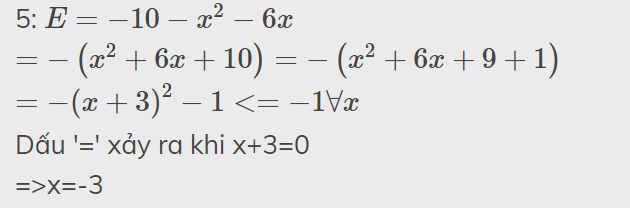
Bài 14:

1: \(A=x^2-x+3\)

\(=x^2-x+\dfrac{1}{4}+\dfrac{11}{4}\)

\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>=\dfrac{11}{4}\forall x\)

Dấu '=' xảy ra khi x-1/2=0

=>\(x=\dfrac{1}{2}\)

2: \(B=x^2+x+1\)

\(=x^2+x+\dfrac{1}{4}+\dfrac{3}{4}\)

\(=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall x\)

Dấu '=' xảy ra khi \(x+\dfrac{1}{2}=0\)

=>\(x=-\dfrac{1}{2}\)

3: \(C=x^2-4x+1\)

\(=x^2-4x+4-3\)

\(=\left(x-2\right)^2-3>=-3\forall x\)

Dấu '=' xảy ra khi x-2=0

=>x=2

4: \(D=x^2-5x+7\)

\(=x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}+\dfrac{3}{4}\)

\(=\left(x-\dfrac{5}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall x\)

Dấu '=' xảy ra khi \(x-\dfrac{5}{2}=0\)

=>\(x=\dfrac{5}{2}\)

5: \(E=x^2+2x+2\)

\(=x^2+2x+1+1=\left(x+1\right)^2+1>=1\forall x\)

Dấu '=' xảy ra khi x+1=0

=>x=-1

6: \(F=x^2-3x+1\)
\(=x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}-\dfrac{5}{4}\)

\(=\left(x-\dfrac{3}{2}\right)^2-\dfrac{5}{4}>=-\dfrac{5}{4}\forall x\)

Dấu '=' xảy ra khi \(x-\dfrac{3}{2}=0\)

=>\(x=\dfrac{3}{2}\)

7: \(G=x^2+3x+3\)

\(=x^2+2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{3}{4}\)

\(=\left(x+\dfrac{3}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall x\)

Dấu '=' xảy ra khi x+3/2=0

=>x=-3/2

8: \(H=3x^2+3-5x\)

\(=3\left(x^2-\dfrac{5}{3}x+1\right)\)

\(=3\left(x^2-2\cdot x\cdot\dfrac{5}{6}+\dfrac{25}{36}+\dfrac{11}{36}\right)\)

\(=3\left(x-\dfrac{5}{6}\right)^2+\dfrac{11}{12}>=\dfrac{11}{12}\forall x\)

Dấu '=' xảy ra khi x-5/6=0

=>x=5/6

9: \(I=4x+2x^2+3\)

\(=2\left(x^2+2x+\dfrac{3}{2}\right)\)

\(=2\left(x^2+2x+1+\dfrac{1}{2}\right)\)

\(=2\left(x+1\right)^2+1>=1\forall x\)

Dấu '=' xảy ra khi x+1=0

=>x=-1

10: \(K=4x^2+3x+2\)

\(=\left(2x\right)^2+2\cdot2x\cdot\dfrac{3}{4}+\dfrac{9}{16}+\dfrac{23}{16}\)

\(=\left(2x+\dfrac{3}{4}\right)^2+\dfrac{23}{16}>=\dfrac{23}{16}\forall x\)

Dấu '=' xảy ra khi 2x+3/4=0

=>x=-3/8

11: M=(x-1)(x-3)+11

\(=x^2-4x+3+11=x^2-4x+14\)

\(=x^2-4x+4+10=\left(x-2\right)^2+10>=10\forall x\)

Dấu '=' xảy ra khi x-2=0

=>x=2

12: \(N=\left(x-3\right)^2+\left(x-2\right)^2\)

\(=x^2-6x+9+x^2-4x+4\)

\(=2x^2-10x+13\)

\(=2\left(x^2-5x+\dfrac{13}{2}\right)=2\left(x^2-5x+\dfrac{25}{4}+\dfrac{1}{4}\right)\)

\(=2\left(x-\dfrac{5}{2}\right)^2+\dfrac{1}{2}>=\dfrac{1}{2}\forall x\)

Dấu '=' xảy ra khi x-5/2=0

=>x=5/2

a: Xét ΔBAE và ΔBDE có

BA=BD

\(\widehat{ABE}=\widehat{DBE}\)

BE chung

Do đó: ΔBAE=ΔBDE

b: ΔBAE=ΔBDE

=>\(\widehat{BAE}=\widehat{BDE}\)

=>\(\widehat{BDE}=90^0\)

=>DE\(\perp\)BC tại D

XétΔBHF vuông tại H và ΔBHC vuông tại H có

BH chung

\(\widehat{HBF}=\widehat{HBC}\)

Do đó ΔBHF=ΔBHC

c: Xét ΔBFC có

BH,CA là các đường cao

BH cắt CA tại E

Do đó: E là trực tâm của ΔBFC
=>FE\(\perp\)BC

mà DE\(\perp\)BC

và FE,DE có điểm chung là E

nên F,E,D thẳng hàng

\(d.\dfrac{59-x}{41}+\dfrac{57-x}{43}=\dfrac{41-x}{59}+\dfrac{43-x}{57}\\ \left(\dfrac{59-x}{41}+1\right)+\left(\dfrac{57-x}{43}+1\right)=\left(\dfrac{41-x}{59}+1\right)+\left(\dfrac{43-x}{57}+1\right)\\ \dfrac{100-x}{41}+\dfrac{100-x}{43}=\dfrac{100-x}{59}+\dfrac{100-x}{57}\\ \left(100-x\right)\left(\dfrac{1}{41}+\dfrac{1}{43}-\dfrac{1}{59}-\dfrac{1}{57}\right)=0\\ 100-x=0\\ x=100\)