\(-x\cdot x=-2\cdot2\)

\(x\cdot x=2\cdot2\)

\(x^2=4\)

\(x^2=2^2\)

\(\Rightarrow x=2.\)

-\(x.x\) = -2.2

\(x^2\)    = 4

\(\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)

Vậy \(x\) \(\in\) {-2; 2}

\(\left(2a-1\right)^{50}=2a-1\)

\(\Rightarrow\left(2a-1\right)^{50}-\left(2a-1\right)=0\)

\(\Rightarrow\left(2a-1\right)\left[\left(2a-1\right)^{49}-1\right]=0\)

\(\Rightarrow\left[{}\begin{matrix}2a-1=0\\\left(2a-1\right)^{49}=1\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}2a-1=0\\2a-1=1\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}2a=1\\2a=2\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}a=\dfrac{1}{2}\\a=1\end{matrix}\right.\)

Từ 1 đến 9 cần 9 chữ số:

Từ 10 đến 99 cần số chữ số là: 2 x [(99 - 10):1 + 1] = 180 (chữ số)

Số các chữ số còn lại là: 300 - (9 + 180) = 111 (chữ số)

Số các số có 3 chữ số là: 111 : 3  =  37

Chữ số 300 trong số đó là chữ thứ 3 của số thứ 37 trong dãy số sau:

     100; 101; 102; 103;..;Số thứ 37 của dãy số trên là:

      1 x (37 - 1) + 100 = 136

Vậy đó là chữ số 6

Kết luận chữ thứ 300 của số mà An viết là chữ số 6.

đây 

Từ 1 đến 9 cần 9 chữ số:

Từ 10 đến 99 cần số chữ số là: 2 x [(99 - 10):1 + 1] = 180 (chữ số)

Số các chữ số còn lại là: 300 - (9 + 180) = 111 (chữ số)

Số các số có 3 chữ số là: 111 : 3  =  37

Chữ số 300 trong số đó là chữ thứ 3 của số thứ 37 trong dãy số sau:

     100; 101; 102; 103;..;Số thứ 37 của dãy số trên là:

      1 x (37 - 1) + 100 = 136

Vậy đó là chữ số 6

Kết luận chữ thứ 300 của số mà An viết là chữ số 6.

Gói thứ nhất mỗi cái kẹo có giá là: 36000 : 8 = 4500 (đồng)

Gói thứ hai mỗi cái kẹo có giá là: 42000 : 12 = 3500 (đồng)

4500 đồng > 3500 đồng vậy giá của mỗi cái kẹo thứ nhất nhiều hơn giá của mỗi cái kẹo thứ hai.

Các cặp phân số bằng nhau: \(\dfrac{2}{4}\)=\(\dfrac{4}{8}\)=\(\dfrac{8}{16}\)=\(\dfrac{16}{32}\)

\(\dfrac{2}{8}\)=\(\dfrac{4}{16}=\dfrac{8}{32}\)

\(\dfrac{4}{2}=\dfrac{8}{4}=\dfrac{16}{8}=\dfrac{32}{16}\)

99 vì dãy số kết thúc ở số 91

99 nhé bạn.

Đề là gì em? So sánh à?

Bạn muốn làm gì với 2 lũy thừa trên(so sánh hay làm gì?)

So sánh: \(5^{36}\) và \(11^{24}\)

Ta có: \(5^{36}=\left(5^3\right)^{12}\) và \(11^{24}=\left(11^2\right)^{12}\)

Vậy \(5^{36}=\left(5^3\right)^{12}=125^{12}\) và \(11^{24}=\left(11^2\right)^{12}=121^{12}\)

Mà \(125^{12}>121^{12}\Rightarrow5^{36}>11^{24}\)

rảnh vx thoi bn ơi

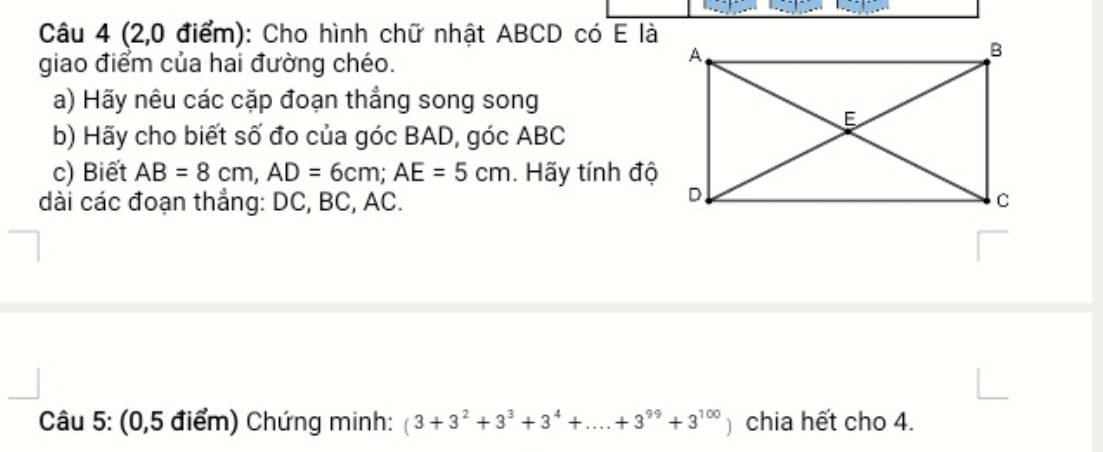
\(\left(3+3^2+3^3+3^4+...+3^{99}+3^{100}\right)\\ =3.\left(1+3\right)+3^3\left(1+3\right)+...+3^{99}\left(1+3\right)\\ =3.4+3^3.4+...+3^{99}.4\\ =4.\left(3+3^3+...+3^{99}\right)⋮4\left(ĐPCM\right)\)

TUI CẦN GẤP