một mảnh vườn hình chữ nhật có chu vi là 10m. người ta làm một lối đi xung quanh rộng 1,5m , phần còn lại để trồng rau có diện tích 459m2. tính diện tích khu vườn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


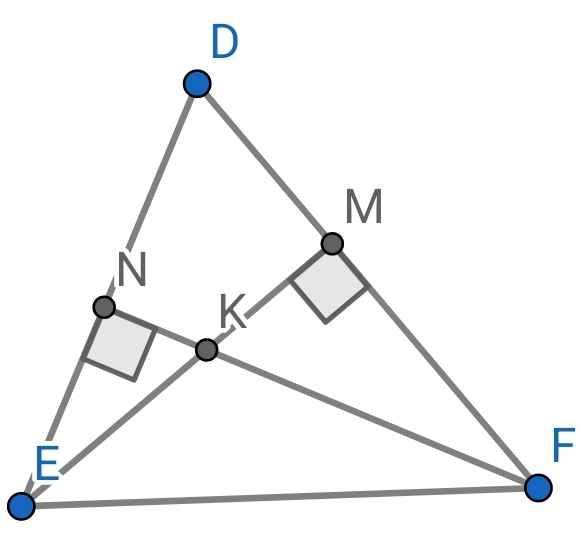
a) Xét hai tam giác vuông: ∆DEM và ∆DFN có:
∠D chung
⇒ ∆DEM ∽ ∆DFN (g-g)
b) Do ∆DEM ∽ ∆DFN (cmt)
⇒ DM/DN = DE/DF
⇒ 6/DN = 8/12
⇒ DN = 6.12 : 8 = 9 (cm)
c) Sửa đề: Chứng minh ∆DNM ∽ ∆DFE
Do DM/DN = DE/DF (cmt)
⇒ DN/DF = DM/DE
Xét ∆DNM và ∆DFE có:
DN/DF = DM/DE (cmt)
∠D chung
⇒ ∆DNM ∽ ∆DFE (c-g-c)

Gọi chiều rộng hình chữ nhật là x(m)
(ĐK: x>0)
Chiều dài hình chữ nhật là 2x(m)
Chiều dài sau khi giảm 2m là 2x-2(m)
Chiều rộng sau khi 2m là x-2(m)
Diện tích giảm đi 116m2 nên ta có:
\(2x^2-\left(2x-2\right)\left(x-2\right)=116\)
=>\(x^2-\left(x-1\right)\left(x-2\right)=116\)
=>\(x^2-\left(x^2-3x+2\right)=116\)
=>3x-2=116
=>3x=118
=>\(x=\dfrac{118}{3}\)(nhận)
Vậy: Chiều rộng là 118/3 m
Chiều dài là \(2\cdot\dfrac{118}{3}=\dfrac{236}{3}\left(m\right)\)

Gọi độ dài quãng đường từ Củ Chi đến Vũng Tàu là x(km)
(Điều kiện: x>0)
Thời gian đi là \(\dfrac{x}{40}\left(giờ\right)\)
Thời gian về là \(\dfrac{x}{40+10}=\dfrac{x}{50}\left(giờ\right)\)
Thời gian đi nhiều hơn thời gian về 27p=0,45 giờ nên ta có:
\(\dfrac{x}{40}-\dfrac{x}{50}=0,45\)
=>\(\dfrac{x}{200}=0,45\)
=>\(x=200\cdot0,45=90\left(nhận\right)\)
Vậy: Độ dài quãng đường từ Củ Chi đến Vũng Tàu là 90km

Quãng đường xe máy đi được sau 1 giờ là: \(45.1=45\left(km\right)\)
Độ dài quãng đường còn lại: \(360-45=315\left(km\right)\)
Tổng vận tốc hai xe: \(45+60=105\) (km/h)
Thời gian kể từ khi ô tô xuất phát đến khi 2 xe gặp nhau là: \(\dfrac{315}{105}=3\) (giờ)
Quãng đường từ chỗ hai xe gặp nhau tới B là: \(60.3=180\left(km\right)\)
Quãng đường từ chỗ hai xe gặp nhau tới A là: \(360-180=180\left(km\right)\)

\(A-B=2.2^{n+1}=2^{n+2}\) là 1 lũy thừa của 2 nên ko chia hết cho 5
\(\Rightarrow A;B\) ko thể đồng thời chia hết cho 5
\(\Rightarrow\) Trong 2 số A, B có tối đa 1 số chia hết cho 5
Do \(16\equiv1\left(mod5\right)\) nên:
TH1: \(n=4k\Rightarrow\left\{{}\begin{matrix}2^{2n+1}=2^{8k+1}=2.\left(16\right)^{2k}\\2^{n+1}=2^{4k+1}=2.\left(16\right)^k\end{matrix}\right.\)
Do \(A=2.\left(16\right)^{2k}+2.\left(16\right)^k+1\equiv2+2+1\left(mod5\right)\equiv0\left(mod5\right)\)
\(\Rightarrow A\) chia hết cho 5 (và hiển nhiên, theo cm ban đầu B sẽ ko chia hết cho 5)
TH2: \(n=4k+1\Rightarrow\left\{{}\begin{matrix}2^{2n+1}=2^{8k+3}=8.\left(16\right)^{2k}\\2^{n+1}=2^{4k+2}=4.\left(16\right)^k\end{matrix}\right.\)
\(\Rightarrow B=8\left(16\right)^{2k}-4.\left(16\right)^k+1\equiv8-4+1\left(mod5\right)\equiv0\left(mod5\right)\)
\(\Rightarrow B\) chia hết cho 5
TH3: \(n=4k+2\Rightarrow\left\{{}\begin{matrix}2^{2n+1}=2^{8k+5}=2.\left(16\right)^{2k+1}\\2^{n+1}=2^{4k+3}=8.\left(16\right)^k\end{matrix}\right.\)
\(B=2.\left(16\right)^{2k+1}-8.\left(16\right)^k+1\equiv2-8+1\left(mod5\right)\equiv0\left(mod5\right)\)
\(\Rightarrow B\) chia hết cho 5
TH4: \(n=4k+3\Rightarrow\left\{{}\begin{matrix}2^{2n+1}=2^{8k+7}=8.\left(16\right)^{2k+1}\\2^{n+1}=\left(16\right)^{k+1}\end{matrix}\right.\)
\(\Rightarrow A=8.\left(16\right)^{2k+1}+\left(16\right)^{k+1}+1\equiv8+1+1\left(mod5\right)\equiv0\left(mod5\right)\)
\(\Rightarrow A\) chia hết cho 5
Vậy với mọi số tự nhiên n thì trong 2 số A và B luôn tồn tại 1 và chỉ 1 số chia hết cho 5

3(x - 2) = ax + 4
3x - 6 = ax + 4
3x - ax = 4 + 6
(3 - a)x = 10
x = 10/(3 - a)
Để nghiệm của phương trình đã cho lớn hơn -1 thì:
10/(3 - a) > -1
3 - a < -10
-a > -10 - 3
-a > -13
a < -13

Em nên viết đề bài bằng công thức toán học có biểu tượng \(\Sigma\) góc trái màn hình.

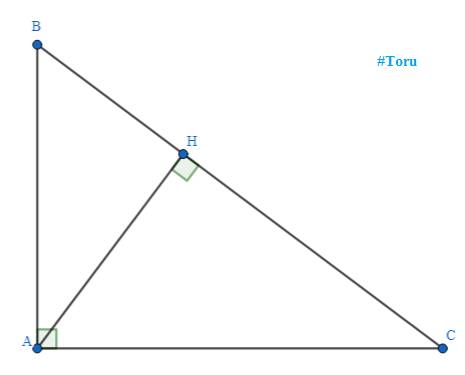
a, Xét \(\Delta HBA\) và \(\Delta ABC\) có:
\(\left\{{}\begin{matrix}\widehat{BHA}=\widehat{BAC}=90^{\circ}\left(AH\bot BC;\Delta ABC\text{ vuông tại }A\right)\\\widehat{ABC}\text{ chung}\end{matrix}\right.\)
\(\Rightarrow \Delta HBA\backsim \Delta ABC(g.g)\)
b, Vì \(\Delta HBA\backsim \Delta ABC(cmt)\Rightarrow \widehat{HAB}=\widehat{ACB}\) (hai góc tương ứng)
hay \(\widehat{HAB}=\widehat{HCA}\) (do \(H\in BC\)>)>
Xét \(\Delta AHB\) và \(\Delta CHA\) có: \(\left\{{}\begin{matrix}\widehat{AHB}=\widehat{CHA}=90^{\circ}\left(AH\bot BC\right)\\\widehat{HAB}=\widehat{HCA}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow \Delta AHB\backsim \Delta CHA(g.g)\Rightarrow \dfrac{AH}{CH}=\dfrac{HB}{HA}\) (các cạnh tương ứng)
\(\Rightarrow AH^2=HB\cdot HC\)

Hàm số bậc nhất có dạng: y = a\(x\) + b
Vì hệ số góc là - 3 nên a = -3 hàm số có dạng:
y = - 3\(x\) + b (d)
Vì hàm số cắt trục hoành tại đểm có hoành độ bằng 2 nên hàm số đó đi qua điểm A(2; 0).
Thay tọa độ điểm A vào phương trình đường thẳng d ta có
-3.2 + b = 0
-6 + b = 0
b = 6
Vậy hàm số có hệ số góc bằng -3 và cắt trục hoành có hoành độ bằng 2 có phương trình là:
y = -3\(x\) + 6
Lời giải:
Gọi chiều dài và chiều rộng khu vườn lần lượt là $a$ và $b$ (m)
Theo bài ra ta có:
$a+b=10:2=5$ (m)
Khi làm lối đi rộng 1,5 m thì phần còn lại là hcn có chiều dài $a-1,5-1,5=a-3$ (m) và chiều rộng $b-1,5-1,5=b-3$ (m)
Diện tích trồng rau là:
$(a-3)(b-3)=459$
$\Leftrightarrow ab-3(a+b)+9=459$
$\Leftrightarrow ab-3.5+9=459$
$\Leftrightarrow ab=465$
$\Leftrightarrow a(5-a)=465$
$\Leftrightarrow a^2-5a+465=0$
$\Leftrightarrow (a-2,5)^2=-458,75<0$ (vô lý)
Do đó không tồn tại khu vườn thỏa mãn đề.