Bài 2. Phân tích các đa thức sau thành nhân tử: a3b-ab3+a2+2ab+b2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Dựng điểm D đối xứng với điểm C qua đường thẳng xy
Gọi giao điểm của CD với xy là H, ta có: \(\widehat{DAH}=\widehat{HAC}\)
Mà \(\widehat{HAC}=\widehat{ACB}\)(Hai góc so le trong)
Còn \(\widehat{ACB}=\widehat{ABC}\)
Do vậy \(\widehat{DAC}+\widehat{CAB}=\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\) hay \(\widehat{BAD}=180^o\)
\(\Rightarrow A;B;D\) là điểm thẳng hàng
Mặt khác \(AD=AC;MD=MC\) do vậy
\(BC+CA+AB=BC+BA+AD=BC+BD< BC+MB+MD=BC+CM+MB\)
\(\Rightarrow Chuvi\Delta ABC< chuvi\Delta MBC\)

3x3 + 6x2 + 3x - 12xy2
= 3x(x2 + 2x + 1 - 4y2)
= 3x[(x + 1)2 - (2y)2]
= 3x(x + 1 + 2y)(x - 2y + 1)
\(3x^3+6x^2+3x-12xy^2\)
\(=3x\left(x^2+2x+1-4y^2\right)\)
\(=3x\left[\left(x+1\right)^2-\left(2y\right)^2\right]\)
\(=3x\left(x+1-2y\right)\left(x+1+2y\right)\)

\(2\left(x+1\right)\left(1-x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\1-x=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=-1\\x=1\end{cases}}\)
Vậy \(S=\left\{-1;1\right\}\)

Bài 2.
\(n^4-2n^3-n^2+2n=n\left(n^3-2n^2-n+2\right)=n\left[n^2\left(n-2\right)-\left(n-2\right)\right]\)
\(=n\left(n-2\right)\left(n^2-1\right)=\left(n-2\right)\left(n-1\right)n\left(n+1\right)\)
là tích của \(4\)số nguyên liên tiếp nên trong đó có ít nhất \(1\)thừa số chia hết cho \(4\), \(1\)thừa số chia hết cho \(3\), \(1\)thừa số chia hết cho \(2\)nhưng không chia hết cho \(4\)
do đó \(A\)chia hết cho \(2.3.4=24\).
Ta có đpcm.
Bài 1:
\(2-x=2\left(x-2\right)^3\)
\(\Leftrightarrow\left(x-2\right)\left[2\left(x-2\right)^2-1\right]=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\2\left(x-2\right)^2=1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=\pm\sqrt{\frac{1}{2}}+2\end{cases}}\)

11, \(a^4-16b^4=\left(a^2+4b^2\right)\left(a^2-4b^2\right)=\left(a^2+4b^2\right)\left(a-2b\right)\left(a+2b\right)\)
12, \(\left(a-b\right)^2-c^2=\left(a-b-c\right)\left(a-b+c\right)\)
13, \(\left(a-2b\right)^2-4b^2=\left(a-2b-2b\right)\left(a-2b+2b\right)=\left(a-4b\right).a\)
14, \(\left(a+3b\right)^2-9b^2=\left(a+3b-3b\right)\left(a+3b+3b\right)=a.\left(a+6b\right)\)
15, \(\left(a-5b\right)^2-16b^2=\left(a-5b-4b\right)\left(a-5b+4b\right)=\left(a-9b\right)\left(a-1\right)\)
16, \(36a^2-\left(3a-2b\right)^2=\left(6a-3a+2b\right)\left(6a+3a-2b\right)=\left(3a+2b\right)\left(9a-2b\right)\)
17, \(4a^2-\left(a+b\right)^2=\left(2a-a-b\right)\left(2a+a+b\right)=\left(a-b\right)\left(3a+b\right)\)
18, \(49a^2-\left(2a-b\right)^2=\left(7a-2a+b\right)\left(7a+2a-b\right)=\left(5a+b\right)\left(9a-b\right)\)

Trả lời:
\(A=2x^2+x=2\left(x^2+\frac{1}{2}x\right)=2\left(x^2+2.x\frac{1}{4}+\frac{1}{16}-\frac{1}{16}\right)\)
\(=2\left[\left(x+\frac{1}{4}\right)^2-\frac{1}{16}\right]=2\left(x+\frac{1}{4}\right)^2-\frac{1}{8}\ge-\frac{1}{8}\forall x\)
Dấu "=" xảy ra khi \(x+\frac{1}{4}=0\Leftrightarrow x=-\frac{1}{4}\)
Vậy \(Min_A=-\frac{1}{8}\Leftrightarrow x=-\frac{1}{4}\)

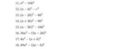
\(a^3b-ab^3+a^2+2ab+b^2\)
\(=\left(a^3b-ab^3\right)+\left(a^2+2ab+b^2\right)\)
\(=ab\left(a^2-b^2\right)+\left(a+b\right)^2\)
\(=ab\left(a-b\right)\left(a+b\right)+\left(a+b\right)^2\)
\(=\left(a+b\right)\left[ab\left(a-b\right)+\left(a+b\right)\right]\)
\(=\left(a+b\right)\left(a^2b-ab^2+a+b\right)\)
Bài 2. Phân tích các đa thức sau thành nhân tử: a3b-ab3+a2+2ab+b2
Giải
a3b-ab3+a2+2ab+b2
= ab(a2-b2)+(a+b)2
= ab(a-b)(a+b)+(a+b)2
= [a2b-ab2+a+b] . (a+b)