những dạng bất phương trình đơn giản thường gặp ở tiểu học. Ở mỗi dạng hãy lấy ví dụ minh họa và hướng dẫn học sinh giải
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


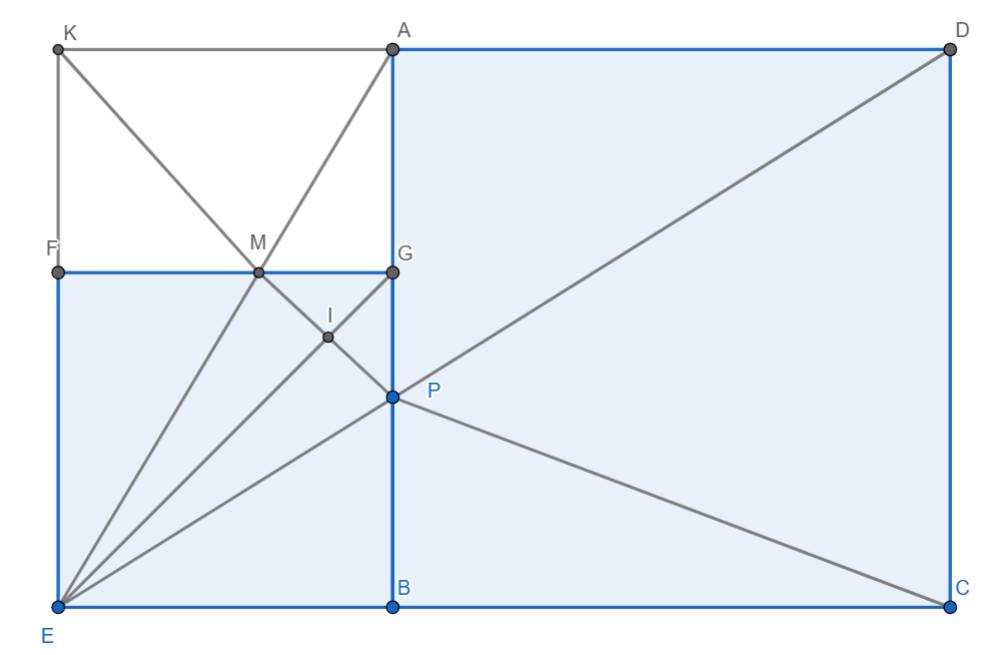
a) \(S_{EAG}=\dfrac{1}{2}\times AG\times ED=\dfrac{1}{2}\times2\times3=3\left(cm^2\right)\)
\(S_{PBC}=\dfrac{1}{2}\times BC\times DC=\dfrac{1}{2}\times5\times5=12,5\left(cm^2\right)\)
b) Ta có:
\(S_{EBC}=\dfrac{1}{2}\times BC\times EC=\dfrac{1}{2}\times5\times8=20\left(cm^2\right)\)
\(S_{PEC}=S_{ECB}-S_{PBC}=20-12,5=7,5\left(cm^2\right)\)
Vậy nên:
\(PD=\dfrac{2\times S_{PEC}}{EC}=\dfrac{2\times7,5}{8}=1,875\left(cm\right)\)
c) Ta thấy:
\(\dfrac{IM}{IP}=\dfrac{S_{MIG}}{S_{IPG}}=\dfrac{S_{MIE}}{S_{IPE}}\) nên \(\dfrac{IM}{IP}=\dfrac{S_{MGE}}{S_{GPE}}=\dfrac{\dfrac{1}{2}\times MG\times3}{\dfrac{1}{2}\times GP\times3}=\dfrac{MG}{GP}\)
Kéo dài AD cắt EF tại K.
Ta có \(S_{AKM}=\dfrac{1}{2}\times3\times2=3\left(cm^2\right)\)
nên \(S_{EKM}=S_{AKE}-S_{AKM}=\dfrac{1}{2}\times3\times5-3=4,5\left(cm^2\right)\)
Vậy \(FM=\dfrac{2\times S_{EKM}}{KE}=1,8\left(cm\right)\)
Thế thì \(MG=3-1,8=1,2\left(cm\right)\)
Lại có \(GP=3-1,875=1,125\left(cm\right)\)
Vậy nên:
\(\dfrac{IM}{IP}=\dfrac{MG}{GP}=\dfrac{1,2}{1,125}=\dfrac{16}{15}\).


a: 11+13+15+17+19
=(11+19)+(13+17)+15
=30+30+15
=75
b: \(122+2116+278+84\)
=(122+278)+(2116+84)
=400+2200
=2600
c: \(12\times125\times54\)
=1500x54
=81000
d: \(27\times36+27\times64=27\times\left(36+64\right)=27\times100=2700\)
e: \(25\text{x}37+25\text{x}63-150\)
=25x(37+63)-150
=25x100-150
=2500-150
=2350
f: \(425\text{x}74-27\text{x}425-1\)
=425x(74-27-1)
=425x46=19550
g: \(8\text{x}9\text{x}14+6\text{x}17\text{x}12+19\text{x}4\text{x}18\)
=14x72+17x72+19x72
=72x(14+17+19)
=50x72=3600
a) $11+13+15+17+19$
$=(11+19)+(13+17)+15$
$=30+30+15$
$=60+15=75$
b) $122+2116+278+84$
$=(122+278)+(2116+84)$
$=400+2200=2600$
c) $12\times125\times54$
$=3\times4\times125\times2\times27$
$=(4\times2)\times125\times(3\times27)$
$=8\times125\times81$
$=1000\times81=81000$
d) $27\times36+27\times64$
$=27\times(36+64)$
$=27\times100=2700$
e) $25\times37+25\times63-150$
$=25\times(37+63)-150$
$=25\times100-150$
$=2500-150=2350$
f) $425\times74-27\times425-425$
$=425\times(74-27-1)$
$=425\times(47-1)$
$=425\times46=19550$
g) $8\times9\times14+6\times17\times12+19\times4\times18$
$=(8\times9)\times14+(6\times12)\times17+(4\times18)\times19$
$=72\times14+72\times17+72\times19$
$=72\times(14+17+19)$
$=72\times(31+19)$
$=72\times50=3600$
$\mathtt{Toru}$

Ta có :
\(\dfrac{1300}{1500}=\dfrac{13}{15}=1-\dfrac{2}{15}\)
\(\dfrac{1333}{1555}=1-\dfrac{222}{1555}\)
Vì \(\dfrac{222}{1555}>\dfrac{2}{15}\)
\(\Rightarrow1-\dfrac{222}{1555}< 1-\dfrac{2}{15}\)
\(\dfrac{\Rightarrow1333}{1555}< \dfrac{1300}{1500}\)

\(\dfrac{29}{2}=\dfrac{28+1}{2}=14+\dfrac{1}{2}=14\dfrac{1}{2}\)
\(\dfrac{15}{4}=\dfrac{12+3}{4}=3+\dfrac{3}{4}=3\dfrac{3}{4}\)
\(\dfrac{31}{2}=\dfrac{30+1}{2}=15\dfrac{1}{2}\)
\(\dfrac{29}{3}=\dfrac{27+2}{3}=9\dfrac{2}{3}\)
\(\dfrac{125}{8}=\dfrac{120+5}{8}=15+\dfrac{5}{8}=15\dfrac{5}{8}\)
\(\dfrac{36}{27}=\dfrac{27+9}{27}=1+\dfrac{9}{27}=1\dfrac{9}{27}\)
\(\dfrac{124}{15}=\dfrac{120+4}{15}=8+\dfrac{4}{15}=8\dfrac{4}{15}\)
\(\dfrac{96}{3}=\dfrac{93+3}{3}=31\dfrac{3}{3}\)
\(\dfrac{129}{24}=\dfrac{120+9}{24}=5+\dfrac{9}{24}=5\dfrac{9}{24}\)
\(\dfrac{78}{13}=\dfrac{65+13}{13}=5+\dfrac{13}{13}=5\dfrac{13}{13}\)
\(\dfrac{91}{4}=\dfrac{88+3}{4}=22+\dfrac{3}{4}=22\dfrac{3}{4}\)
\(\dfrac{115}{8}=\dfrac{112+3}{8}=14+\dfrac{3}{8}=14\dfrac{3}{8}\)

a: \(B=2021\times2025=\left(2023-2\right)\times\left(2023+2\right)=2023\times2023-2\times2\)
=>\(B=A-4\)
=>A lớn hơn B 4 đơn vị
b: \(C=35\times53-18=35\times35+35\times18-18\)
\(=35\times35+18\times\left(35-1\right)\)
\(=35\times35+18\times34\)
\(D=35+53\times34\)
\(=35+\left(35-1\right)\times\left(35+18\right)\)
\(=35+35\times35+35\times18-35\times1-18\)
\(=35\times35+35\times17+17=35\times35+36\times17\)
\(=35\times35+18\times34\)
=C
=>C=D

Gọi số cần tìm có dạng là \(X=\overline{ab}\)
Vì viết thêm số 7 vào bên trái số đó thì sẽ được số mới gấp 36 lần số cần tìm nên ta có: \(\overline{7ab}=36\times\overline{ab}\)
=>\(700+\overline{ab}=36\times\overline{ab}\)
=>\(35\times X=700\)
=>X=20
Vậy: Số cần tìm là 20
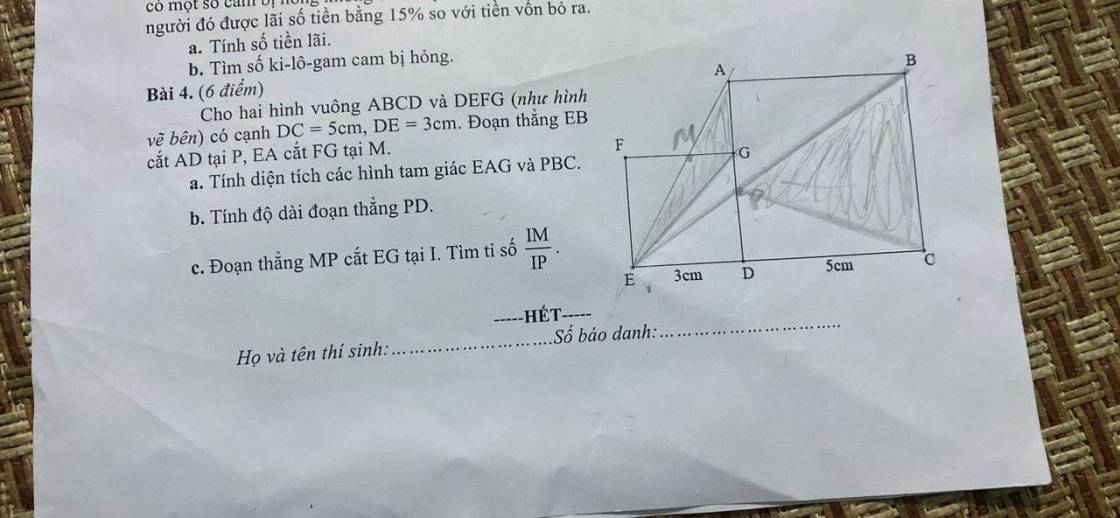
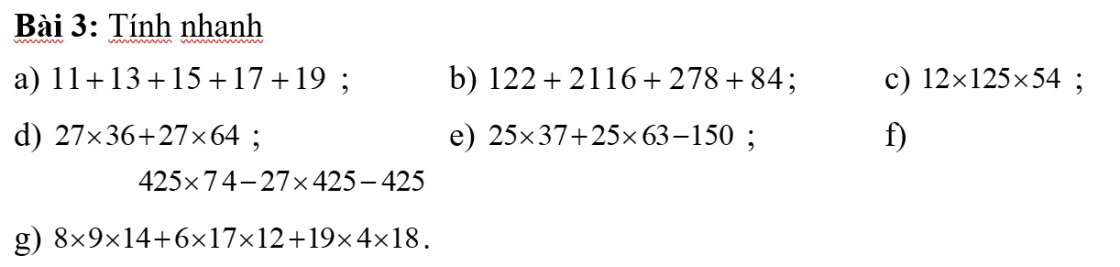
 dạo này nhìu btvn quá , nhờ mn 1 tí nhá
dạo này nhìu btvn quá , nhờ mn 1 tí nhá