Cho tam giác ABC có ba góc nhọn và AB<AC. Kẻ các đường cao BE,CF (E ∈∈ AB), gọi H là giao điểm của BE với CF.
a) Chứng minh rằng AFHE là tứ giác nội tiếp.
b) Gọi D =AHˆADF���^ +...
Đọc tiếp
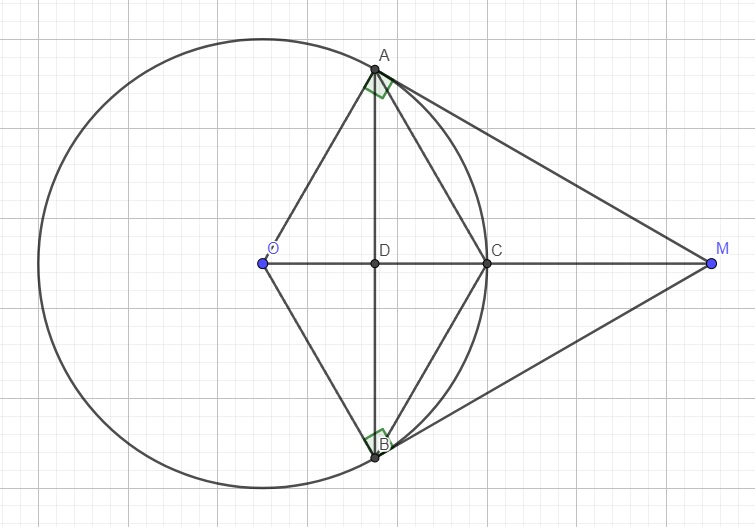
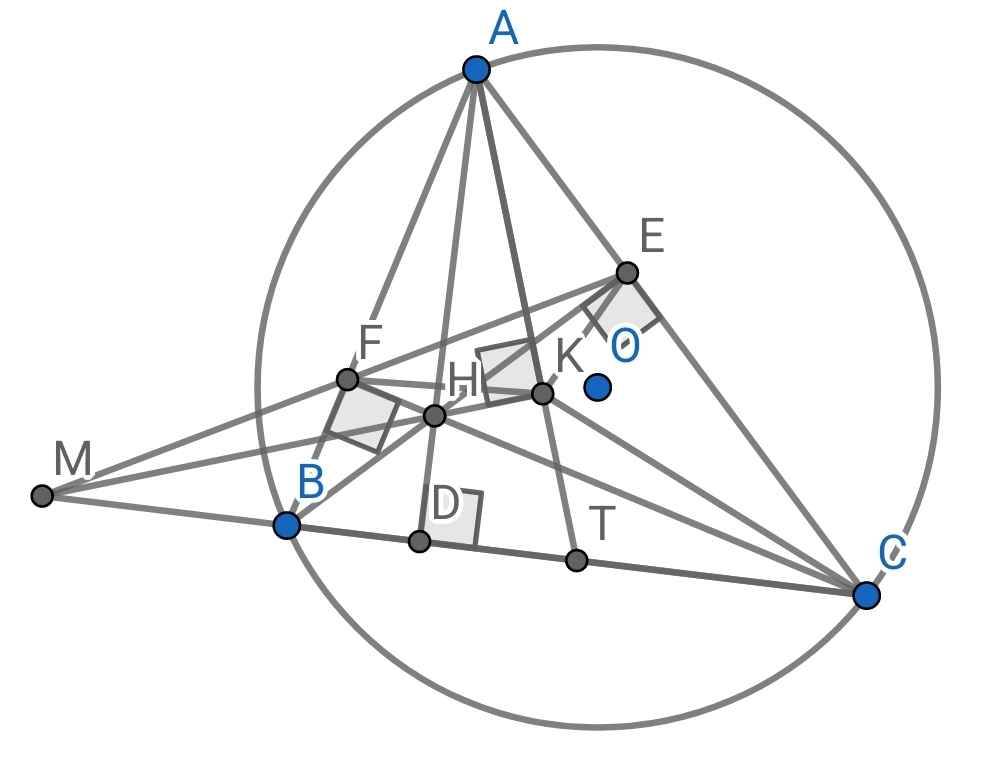
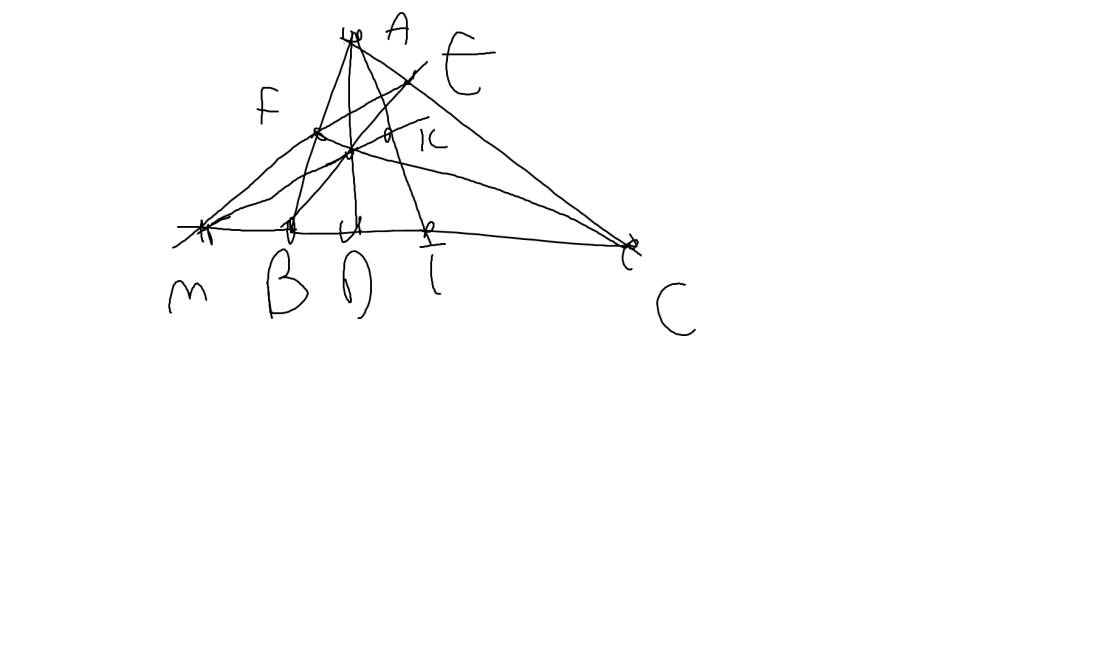
Cho tam giác ABC có ba góc nhọn và AB<AC. Kẻ các đường cao BE,CF (E ∈∈ AC; F ∈∈ AB), gọi H là giao điểm của BE với CF.
a) Chứng minh rằng AFHE là tứ giác nội tiếp.
b) Gọi D =AH∩∩ BC, chứng minh rằng AFDC là tứ giác nội tiếp vàˆADF���^ + ˆBC��^ =90°.
c) Kẻ hai tiếp tuyến AP,AQ tới đường tròn đường kính BC (P,Q là các tiếp điểm). Chứng minh rằng APDQ là tứ giác nội tiếp và ba điểm P,H.Q thẳng hàng.







Ở câu b, đề là \(\widehat{ADF}+\) cái gì \(=90^0\) độ em ha?