Số có hai chữ số có dạng: \(\overline{ab}\) 

Khi viết thêm vào bên phải số đó hai chữ số: c;d

Thì được số mới có dạng: \(\overline{abcd}\)

Theo bài ra ta có: \(\overline{abcd}\) - \(\overline{ab}\) = 1995

                            \(\overline{ab}\) \(\times\) 100 + \(\overline{cd}\) - \(\overline{ab}\) = 1995

                            \(\overline{ab}\) \(\times\) ( 100 - 1) + \(\overline{cd}\) = 1995

                            \(\overline{ab}\) \(\times\) 99 + \(\overline{cd}\)         = 1995

                           \(\overline{ab}\) \(\times\) 99 = 1995 - \(\overline{cd}\)

                           \(\overline{ab}\)        = \(\dfrac{1995-\overline{cd}}{99}\) 

                           \(\overline{ab}\)   = 20 - \(\dfrac{cd-15}{99}\)

                          ⇒ \(\overline{cd}\) - 15 ⋮ 99  vì \(\overline{cd}\) ≤ 99 ⇒ \(\overline{cd}\)  = 15; 

                           \(\overline{ab}\) = 20

Vậy số có hai chữ số ban đầu là 20; hai chữ số viết thêm là: 15

Trong hai giờ ô tô đi được tất cả là: \(\dfrac{2}{6}\) + \(\dfrac{3}{7}\) =  \(\dfrac{16}{21}\) (quãng đường)

Đáp số: \(\dfrac{16}{21}\) (quãng đường)

Giả sử ta coi số hsinh giỏi là 2 phần bằng nhau, số hsinh khá là 3 phần cũng bằng nhau và số hsinh trung bình là 4 phần như vậy.

Tổng số phần bằng nhau là: 2+4+3=9 (phần)

Ta có: Nếu hsinh yếu là 4 bạn thì số hsinh giỏi, khá và trung bình là 37 bạn. Mà 37 không chia hết cho 9 nên số hsinh yếu là 5 bạn hsinh.

Số hsinh giỏi là: (41-5):9x2=8 (hsinh)

Số hsinh khá là: 8:2x3=12 (hsinh)

Số hsinh trung bình là: 12:3x4=16(hsinh)

đ/s:...

Vì số học sinh giỏi bằng \(\dfrac{2}{3}\) số học sinh khá nên số học sinh khá phải chia hết cho 3.

Số học sinh trung bình bằng: 1 : \(\dfrac{3}{4}\) = \(\dfrac{4}{3}\) (số học sinh khá)

Tổng số học sinh giỏi, khá, trung bình bằng:

             \(\dfrac{2}{3}\) + 1 + \(\dfrac{4}{3}\) = 3 (lần số học sinh khá)

Vì số học sinh cả lớp bớt đi số học sinh kém sẽ gấp 3 lần số học sinh khá.

Nên số học sinh cả lớp bớt đi số học sinh kém phải chia hết cho 3

                  41 : 3 = 13 dư 2

Vậy số học sinh kém phải là 2 hoặc 5

Nếu số học sinh kém là 2 thì số học sinh khá  là:

                ( 41 - 2): 3 = 13 (loại vì không chia hết cho 3)

Nếu số học sinh kém là 5 thì số học sinh khá là:

                ( 41 - 5): 3 = 12 (học sinh)

Số học sinh giỏi là: \(\dfrac{2}{3}\) \(\times\) 12 = 8 (học sinh)

Số học sinh trung bình là: 12 \(\times\) \(\dfrac{4}{3}\) = 16 (học sinh)

Đáp số: Số học sinh giỏi 8 học sinh

             Số học sinh khá 12 học sinh

             Số học sinh trung bình là 16 học sinh

             Số học sinh kém là 5 học sinh

\(\left(12\cdot15-x\right)\cdot\dfrac{1}{4}=120\cdot\dfrac{1}{4}\)

\(\Rightarrow\left(180-x\right)\cdot\dfrac{1}{4}=30\)

\(\Rightarrow180-x=30:\dfrac{1}{4}\)

\(\Rightarrow180-x=120\)

\(\Rightarrow x=180-120\)

\(\Rightarrow x=60\)

Bài 1:

a) Sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác OAB, OBC,OCD và ODA.

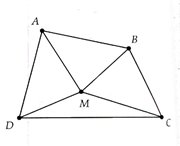
b) Chứng minh tổng hai đường chéo lớn hơn nửa chu vi tứ giác sử dụng kết quả của a).

Chứng minh tổng hai đường chéo nhỏ hơn chu vi tứ giác sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác ABC, ADC, ABD và CBD

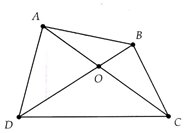
Bài 3:

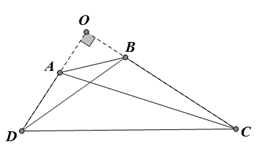
Gọi O là giao điểm AD và BC.

Ta có $\hat{C}+\stackrel{⌢}{D}={90}^0$ nên $\hat{O}={90}^0$

Áp dụng định lí Py – ta – go,

Ta có 

$A{C}^2=O{A}^2+O{C}^2.$

$B{D}^2=O{B}^2+O{D}^2$

Nên $A{C}^2+B{D}^2=\left(O{A}^2+O{B}^2\right)+\left(O{C}^2+O{D}^2\right)=A{B}^2+C{D}^2$

Bài 1: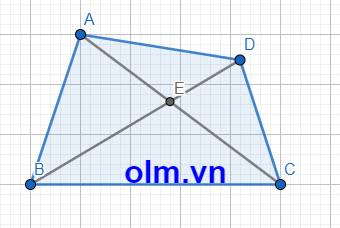 

Gọi E là giao điểm của hai đường chéo AC và BD 

Xét tam giác AEB ta có: AE + BE > AB (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)

Xét tam giác DEC ta có: DE + CE > DC (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)

Cộng vế với vế ta có: AE + BE + DE + CE > AB + DC 

                                  (AE + CE) + (BE + DE) > AB + DC

                                     AC + BD > AB + DC 

Tương tự ta có AC + BD > AD + BC 

Kết luận: Trong một tứ giác tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối.

Nửa chu vi của tứ giác ABCD là: \(\dfrac{AB+BC+CD+DA}{2}\)

Theo chứng minh trên ta có:

 \(\dfrac{AB+BC+CD+DA}{2}\)< \(\dfrac{\left(AB+CD\right)\times2}{2}\) = AB + CD (1)

Vì trong một tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại nên ta có:

AB + AD > BD 

AB + BC > AC

BC + CD > BD 

CD + AD > AC 

Cộng vế với vế ta có:

(AB + BC + CD + DA)\(\times\)2 > (BD + AC ) \(\times\) 2

⇒AB + BC + CD + DA > BD + AC  (2)

Kết hợp (1) và (2) ta có:

Tổng hai đường chéo của tứ giác lớn hơn nửa chu vi của tứ giác nhưng nhỏ hơn chu vi của tứ giác

\(3\cdot x+1^2=100\)

\(\Rightarrow3\cdot x+1=100\)

\(\Rightarrow3\cdot x=100-1\)

\(\Rightarrow3\cdot x=99\)

\(\Rightarrow x=\dfrac{99}{3}\)

\(\Rightarrow x=33\)

Gọi số chính phương là a² ( a ϵ N* )

Ta có n² + 2026 = a²

Vì 2025 < 2026 < 2116 ⇒ 45² < 2026 < 46²

Suy ra 2026 không phải số chính phương 

Vậy không có giá trị tự nhiên nào của n thỏa mãn n² + 2026 là số chính phương

Đặt \(n^2+2026=a^2\left(a\in Z\right)\)

\(\Rightarrow n^2-a^2=2026\)

\(\Rightarrow\left(n-a\right)\left(n+a\right)=2026\left(1\right)\)

Ngoài ra ta có :

\(\left(n+a\right)+\left(n-a\right)=2n⋮2\)

\(\Rightarrow n+a⋮2;n-a⋮2\)

\(\Rightarrow\left(n+a\right)\left(n-a\right)⋮4\)

mà 2026 không chia hết cho 4

⇒ (1) không thỏa

⇒ Không có n nào để \(n^2+2026\) là số chính phương

`@` `\text {Ans}`

`\downarrow`

`-4/5 - 1/2 = -x`

`=> -8/10 - 5/10 = -x`

`=> -13/10 = -x`

`=> x = 13/10 = 1,3`

Vậy, `x = 1,3.`

\(-\dfrac{4}{5}-\dfrac{1}{2}=-x\)

\(-\dfrac{13}{10}=-x\)

\(x=\dfrac{13}{10}\)

Vậy \(x=\dfrac{13}{10}\)