Tìm nϵN sao cho 12n+8⋮(4n+1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(4=2^2\)
\(6=2\cdot3\)
\(9=3^2\)
\(\Rightarrow BCNN\left(4,6,9\right)=2^2\cdot3^2=4\cdot9=36\)
\(B\left(36\right)=\left\{36;...;468;504;540\right\}\)
\(B\left(36\right)+2=\left\{38;...470;506;542\right\}\)
Số cần tìm trong tập B(36)+2 là số lớn hơn 450 và không lớn hơn 500.
Vậy số học sinh của khối là 470

An và Bình cùng đếm số trái cây mình có, An nói: “Nếu cậu cho mình 4 trái thì 2 tụi mình sẽ có số trái cây bằng nhau”. Bình nói lại với An: “Còn nếu cậu cho mình 2 trái thì số trái cây của tớ sẽ gấp 4 lần cậu”. Hỏi mỗi bạn có bao nhiêu trái

\(A=2^0+2^1+2^2+...+2^{20}\)
\(2A=2^1+2^2+2^3+...+2^{21}\)
\(A=2^{21}-1\)
Vậy \(A>B\)

Lời giải:
$\overline{abcabc}=\overline{abc}\times 1000+\overline{abc}$
$=\overline{abc}\times (1000+1)=\overline{abc}\times 1001=\overline{abc}\times 143\times 7\vdots 7$
Ta có đpcm.

Lời giải:
$16^x=16^{x^3}$
$\Rightarrow x=x^3$
$\Rightarrow x^3-x=0$
$\Rightarrow x(x^2-1)=0$
$\Rightarrow x=0$ hoặc $x^2-1=0$
$\Rightarrow x=0$ hoặc $x^2=1$
$\Rightarrow x=0$ hoặc $x=1$ hoặc $x=-1$

\(2x-2^0=3^5:3^3\\\Rightarrow 2x-1=3^2\\\Rightarrow2x-1=9\\\Rightarrow2x=9+1\\\Rightarrow 2x=10\\\Rightarrow x=10:2\\\Rightarrow x=5\\Vậy:x=5\)

4x + 18:2 = 13
=> 4x + 9 = 13
=> 4x = 13 - 9 = 4
=> x = 4÷4
=> x =1

Xét TH n3 lẻ => n lẻ =>n3+n +1 là lẻ ( n3+n chẵn +1 là lẻ)
n3chẵn =>n chẵn => n3+n+1 là lẻ
=>n^3+n+1 k chia hết cho 2 và 4

\(a,A=2+2^2+2^3+...+2^{100}\)
\(=\left(2+2^2\right)+\left(2^3+2^4\right)+\left(2^5+2^6\right)...+\left(2^{99}+2^{100}\right)\)
\(=6+2^2\cdot\left(2+2^2\right)+2^4\cdot\left(2+2^2\right)...+2^{98}\cdot\left(2+2^2\right)\)
\(=6+2^2\cdot6+2^4\cdot6...+2^{98}\cdot6\)
\(=6\cdot\left(1+2^2+2^4+...+2^{98}\right)\)
Vì \(6\cdot\left(1+2^2+2^4+...+2^{98}\right)⋮6\)
nên \(A⋮6\)
\(b,A=2+2^2+2^3+...+2^{100}\)
\(=\left(2+2^3\right)+\left(2^2+2^4\right)+\left(2^3+2^5\right)+...+\left(2^{97}+2^{99}\right)+\left(2^{98}+2^{100}\right)\)
\(=10+2\cdot\left(2+2^3\right)+2^2\cdot\left(2+2^3\right)+...+2^{96}\cdot\left(2+2^3\right)+2^{97}\cdot\left(2+2^3\right)\)
\(=10+2\cdot10+2^2\cdot10+...+2^{96}\cdot10+2^{97}\cdot10\)
\(=10\cdot\left(1+2+2^2+...+2^{96}+2^{97}\right)\)
Vì \(10\cdot\left(1+2+2^2+...+2^{96}+2^{97}\right)⋮10\)
nên \(A⋮10\)
#\(Toru\)
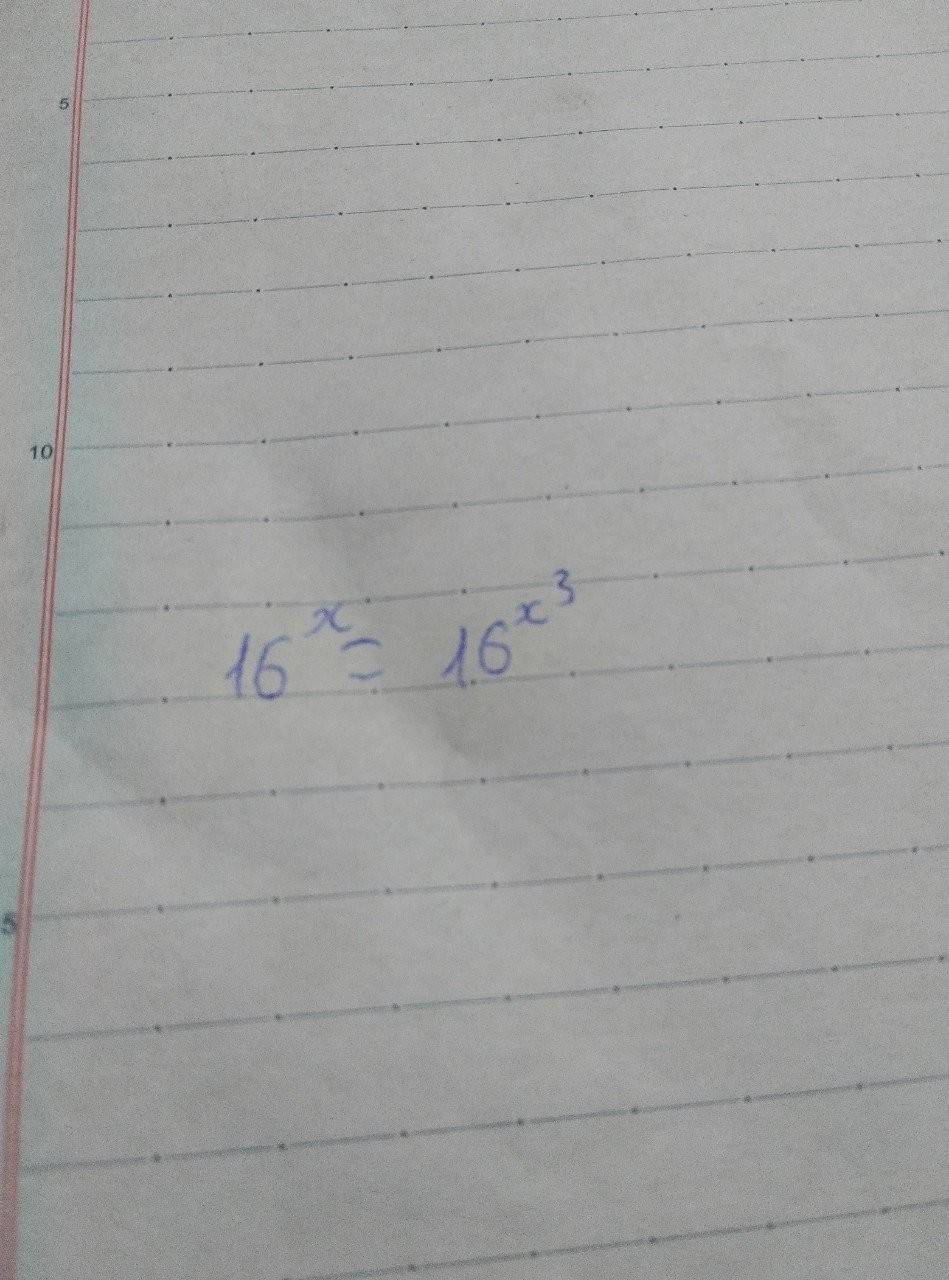
Lời giải:
$12n+8\vdots 4n+1$
$\Rightarrow 3(4n+1)+5\vdots 4n+1$
$\Rightarrow 5\vdots 4n+1$
Do $4n+1>0$ với mọi $n\in\mathbb{N}$ nên:
$\Rightarrow 4n+1\in\left\{1; 5\right\}$
$\Rightarrow n\in\left\{0; 1\right\}$ (đều thỏa mãn)