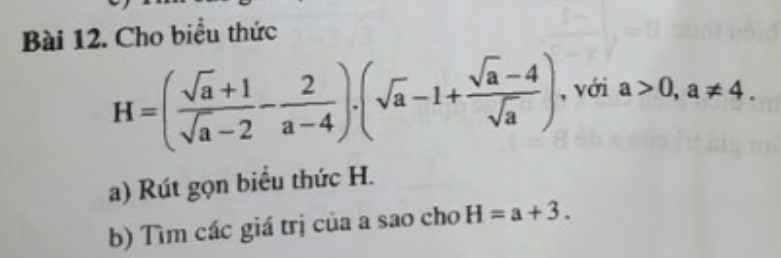
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng BĐT Cô-si:
\(\sqrt{3x+2y+z}+\sqrt{3y+2z+x}+\sqrt{3z+2x+y}\)
\(=\dfrac{1}{2\sqrt{6}}.\left(2.\sqrt{6}.\sqrt{3x+2y+z}+2.\sqrt{6}.\sqrt{3y+2z+x}+2.\sqrt{6}.\sqrt{3z+2x+y}\right)\)
\(\le\dfrac{1}{2\sqrt{6}}\left(6+3x+2y+z+6+3y+2z+x+6+3z+2x+y\right)\)
\(=\dfrac{1}{2\sqrt{6}}\left(6x+6y+6z+18\right)=\dfrac{36}{2\sqrt{6}}=3\sqrt{6}\) (đpcm)
Dấu "=" xảy ra khi \(x=y=z=1\)
cho pt x^2-2(m-1)x+m^2+2,m la ham so.tim m để pt co 2no pb x1,x2 thỏa mãn:x1^2-3x2^2=2.(m^2+x1.x2-1)


a: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
=>\(\widehat{BFE}+\widehat{BCE}=180^0\)
mà \(\widehat{BFE}+\widehat{AFE}=180^0\)(hai góc kề bù)
nên \(\widehat{AFE}=\widehat{ACB}\)
b: Gọi Ax là tiếp tuyến tại A của (O)
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\)
mà \(\widehat{ABC}=\widehat{AEF}\left(=180^0-\widehat{FEC}\right)\)
nên \(\widehat{xAC}=\widehat{AEF}\)
=>FE//Ax
=>IK//Ax
Xét (O) có
\(\widehat{xAK}\) là góc tạo bởi tiếp tuyến Ax và dây cung AK
\(\widehat{AIK}\) là góc nội tiếp chắn cung AK
Do đó: \(\widehat{xAK}=\widehat{AIK}\)
mà \(\widehat{xAK}=\widehat{AKI}\)(IK//Ax)
nên \(\widehat{AIK}=\widehat{AKI}\)
=>\(sđ\stackrel\frown{AK}=sđ\stackrel\frown{AI}\)
Xét (O) có
\(\widehat{ACK}\) là góc nội tiếp chắn cung AK
\(\widehat{AKI}\) là góc nội tiếp chắn cung AI
\(sđ\stackrel\frown{AK}=sđ\stackrel\frown{AI}\)
Do đó: \(\widehat{ACK}=\widehat{AKI}\)
Xét ΔACK và ΔAKE có
\(\widehat{ACK}=\widehat{AKE}\)
\(\widehat{CAK}\) chung
Do đó ΔACK~ΔAKE
=>\(\dfrac{AC}{AK}=\dfrac{AK}{AE}\)
=>\(AK^2=AC\cdot AE\)

∆ = (2m + 1)² - 4.1.(m² + 3m)
= 4m² + 4m + 1 - 4m² - 12m
= -8m + 1
Để phương trình có hai nghiệm phân biệt thì ∆ > 0
⇔ -8m + 1 > 0
⇔ m < 1/8
Theo hệ thức Vi-ét, ta có:
x₁ + x₂ = -(2m + 1)
x₁x₂ = m² + 3m
Q = x₁² + x₂² = (x₁ + x₂)² - 2x₁x₂
= [-(2m + 1)]² - 2(m² + 3m)
= 4m² + 4m + 1 - 2m² - 6m
= 2m² - 2m + 1
= 2(m² - m + 1/2)
= 2(m² - 2.m.1/2 + 1/4 + 1/4)
= 2(m - 1/2)² + 1/2
Do (m - 1/2)² ≥ 0 với mọi x ∈ R
⇒ 2(m - 1/2)² ≥ 0 với mọi x ∈ R
⇒ 2(m - 1/2)² + 1/2 ≥ 1/2
⇒ Q nhỏ nhất là 1/2 khi m = 1/2 (không thỏa mãn m < 1/8)
Vậy không tìm được m để Q nhỏ nhất

Giải:
Gọi chiều dài là \(x\) (m); \(x\) > 0
Nửa chu vi của hình chữ nhật là: 340 : 2 = 170 (m)
Chiều rộng của hình chữ nhật là: 170 - \(x\) (m)
Ba lần chiều dài của hình chữ nhật là: \(x\times\) 3 = 3\(x\) (m)
Bốn lần chiều rộng của hình chữ nhật là: (170 - \(x\)) \(\times\) 4 = 680 - 4\(x\)(m)
Theo bài ra ta có phương trình:
3\(x\) - (680 - 4\(x\)) = 20
3\(x\) - 680 + 4\(x\) = 20
7\(x\) - 680 = 20
7\(x\) = 20 + 680
7\(x\) = 700
\(x\) = 700 : 7
\(x\) = 100
Vậy chiều dài của hình chữ nhật là: 100 m
Chiều rộng của hình chữ nhật là: 170 - 100 = 70 (m)
Kết luận: Chiều dài của hình chữ nhật là 100 m
Chiều rộng của hình chữ nhật là 70 m

a: Gọi phương trình đường thẳng AB là (d): y=ax+b
Thay x=5 và y=2 vào y=ax+b, ta được:
\(a\cdot5+b=2\)(1)
Thay x=3 và y=-4 vào y=ax+b, ta được:
\(a\cdot3+b=-4\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}5a+b=2\\3a+b=-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a=6\\5a+b=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=3\\b=2-5a=2-5\cdot3=-13\end{matrix}\right.\)
Vậy: AB: y=3x-13
b: M thuộc trục hoành nên M(x;0)
M(x;0); A(5;2); B(3;-4)
\(MA=\sqrt{\left(5-x\right)^2+\left(2-0\right)^2}=\sqrt{\left(x-5\right)^2+4}\)
\(MB=\sqrt{\left(3-x\right)^2+\left(-4-0\right)^2}=\sqrt{\left(x-3\right)^2+16}\)
ΔMAB cân tại M
=>MA=MB
=>\(\left(x-5\right)^2+4=\left(x-3\right)^2+16\)
=>\(\left(x-5\right)^2-\left(x-3\right)^2=12\)
=>\(x^2-10x+25-x^2+6x-9=12\)
=>-4x+16=12
=>-4x=-4
=>x=1
vậy: M(1;0)

a: A(-2;0); B(0;4); C(1;1); D(-3;2)
\(\overrightarrow{AB}=\left(2;4\right);\overrightarrow{AD}=\left(-1;2\right)\)
Vì \(\dfrac{2}{-1}\ne2=\dfrac{4}{2}\)
nên A,B,D không thẳng hàng
\(\overrightarrow{AB}=\left(2;4\right);\overrightarrow{AC}=\left(3;1\right)\)
Vì \(\dfrac{2}{3}\ne\dfrac{4}{1}\)
nên A,B,C không thẳng hàng
b: \(AB=\sqrt{2^2+4^2}=2\sqrt{5};AC=\sqrt{3^2+1^2}=\sqrt{10}\)
\(BC=\sqrt{\left(1-0\right)^2+\left(1-4\right)^2}=\sqrt{10}\)
Vì \(CA^2+CB^2=AB^2\)
nên ΔCAB vuông tại C
=>\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}\cdot10=5\)

Xét ΔABC vuông tại A có \(cosABC=\dfrac{AB}{BC}\)
=>\(\dfrac{2}{BC}=cos60=\dfrac{1}{2}\)
=>BC=4(cm)
Xét ΔAHB vuông tại H có \(sinB=\dfrac{AH}{AB}\)
=>\(\dfrac{AH}{2}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(AH=\sqrt{3}\left(cm\right)\)
a: \(H=\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{2}{a-4}\right)\cdot\left(\sqrt{a}-1+\dfrac{\sqrt{a}-4}{\sqrt{a}}\right)\)
\(=\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{2}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\right)\cdot\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)+\sqrt{a}-4}{\sqrt{a}}\)
\(=\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}+2\right)-2}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\cdot\dfrac{a-4}{\sqrt{a}}\)
\(=\dfrac{a+3\sqrt{a}}{\sqrt{a}}=\sqrt{a}+3\)
b: H=a+3
=>\(a+3=\sqrt{a}+3\)
=>\(a-\sqrt{a}=0\)
=>\(\sqrt{a}\left(\sqrt{a}-1\right)=0\)
=>\(\left[{}\begin{matrix}a=0\left(loại\right)\\a=1\left(nhận\right)\end{matrix}\right.\)