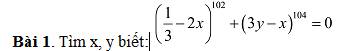có ba kho thóc sau khi chuyển đi 1/5 số thóc ở kho 1, 1/6 số thóc ở kho 2 và 1/11 số thóc ở kho 3 thì tổng số thóc ở ba kho là 600 tấn biết số thóc ở cả ba kho là như nhau tìm tổng số thóc của cả ba kho lúc ban đầu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$\frac{2a+b+c+d}{a}=\frac{a+2b+c+d}{b}=\frac{a+b+2c+d}{c}=\frac{a+b+c+2d}{d}$
$\Rightarrow 1+\frac{a+b+c+d}{a}=1+\frac{a+b+c+d}{b}=1+\frac{a+b+c+d}{c}=1+\frac{a+b+c+d}{d}$
$\Rightarrow \frac{a+b+c+d}{a}=\frac{a+b+c+d}{b}=\frac{a+b+c+d}{c}=\frac{a+b+c+d}{d}$
$\Rightarrow a+b+c+d=0$ hoặc $a=b=c=d$
Nếu $a+b+c+d=0$ thì:
$M=\frac{a+b}{-(a+b)}+\frac{b+c}{-(b+c)}+\frac{c+d}{-(c+d)}+\frac{d+a}{-(d+a)}=(-1)+(-1)+(-1)+(-1)=-4$
Nê $a=b=c=d$ thì:
$M=\frac{a+a}{a+a}+\frac{a+a}{a+a}+\frac{a+a}{a+a}+\frac{a+a}{a+a}$
$=1+1+1+1=4$

Lời giải:
a. Chiều dài mới bằng $100+30=130$ % chiều dài cũ.
Chiều rộng mới bằng $100+20=120$ % chiều rộng cũ.
Diện tích mới bằng: $130.120:100=156$ (%) diện tích cũ.
Diện tích sân vận động tăng $156-100=56$ %
b.
30% chiều dài sân vận động tăng thêm ứng với 60 m
Suy ra chiều dài sân vận động ban đầu là: $60:30.100=200$ (m)
Chiều rộng sân vận động ban đầu: $200\times 3:4=150$ (m)

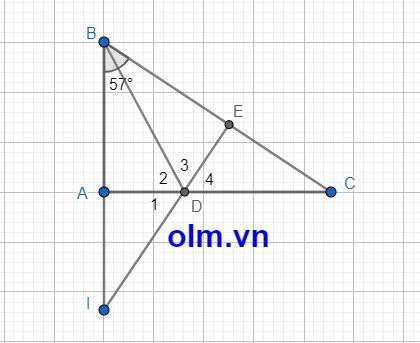
Xét tam giác ABD và tam giác EBD có
\(\widehat{ABD}\) = \(\widehat{EBD}\) (gt)
AB = BE (gt)
BD chung
⇒\(\Delta\)ABD = \(\Delta\) EBD (c-g-c)
⇒AD = DE
⇒ \(\widehat{BAD}\) = \(\widehat{BED}\) = 900
\(\widehat{DEC}\) = 1800 - 900 = 900
Xét tam giác ADI và tam giác EDC có:
\(\widehat{DAI}\) = \(\widehat{DEC}\) = 900 (cmt)
AD = DE (cmt)
AI = EC (gt)
⇒ \(\Delta\)ADI = \(\Delta\)EDC (c-g-c)
⇒ D1 = D4
Mà D2 + D3 + D4 = 1800
⇒ D1 + D2 + D3 = 1800
⇒ \(\widehat{IDE}\) = 1800
⇒ I;D;E thẳng hàng (đpcm)
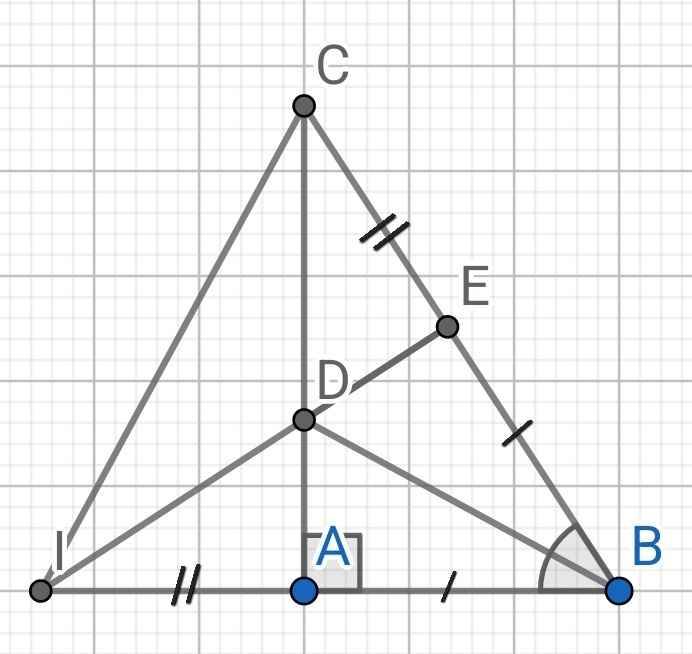 Do BD là tia phân giác của ∠ABC (gt)
Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠EBD
Xét ∆ABD và ∆EBD có:
AB = BE (gt)
∠ABD = ∠EBD (cmt)
BD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
⇒ ∠BAD = ∠BED = 90⁰ (hai góc tương ứng)
⇒ DE ⊥ BC
Do AI = EC (gt)
AB = BE (gt)
⇒ BI = AI + AB = BE + EC = BC
∆BCI có:
BI = BC (cmt)
⇒ ∆BCI cân tại B
Mà BD là tia phân giác của ∠ABC
⇒ BD là tia phân giác của ∠IBC
⇒ BD là đường cao của ∆BCI
Lại có:
CA ⊥ AB (∆ABC vuông tại A)
CA ⊥ BI
⇒ CA là đường cao thứ hai của ∆BCI
⇒ ID là đường cao thứ ba của ∆BCI
⇒ ID ⊥ BC
Mà DE ⊥ BC (cmt)
⇒ I, D, E thẳng hàng

A = \(\dfrac{2}{x^2+1}\)
A \(\notin\) Z ⇔ 2 không chia hết \(x^2\) + 1
⇒ \(x^2\) + 1 \(\notin\) Ư(2)
Ư(2) = 1; 2
⇒ \(x^2\) + 1 ≠ 1; 2
th1: \(x^2\) + 1 ≠ 1 ⇒ \(x\)≠ 0;
th2 \(x^2\) + 1 ≠ 2 ⇒ \(x\) \(\ne\) 1 ⇒ \(x\) ≠ \(\pm\) 1
Vây \(x\) \(\ne\) -1; 0; 1

(1/3 - 2x)¹⁰² + (3y - x)¹⁰⁴ = 0
⇒ 1/3 - 2x = 0 và 3y - x = 0
*) 1/3 - 2x = 0
2x = 1/3
x = 1/3 : 2
x = 1/6
*) 3y - x = 0
3y - 1/6 = 0
3y = 1/6
y = 1/6 : 3
y = 1/18
Vậy x = 1/6; y = 1/18