Chứng minh rằng
\(\dfrac{3}{1^2\text{x }2^2}+\dfrac{5}{2^2\text{x }3^2}+\dfrac{7}{3^2\text{x }4^2}+...+\dfrac{19}{9^2\text{x }10^2}< 1.\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do hình vuông có 4 cạnh nên ta lấy 3x4=12
đáp án là D.12 lần
Gọi cạnh ban đầu của hình vuông là `a`
`=>` Chu vi ban đầu của hình vuông là `C_{t}=4a` `(1)`
Tăng cạnh hình vuông gấp `3` lần thì cạnh hình vuông lúc này là `3 \times a`
`=>` Chu vi sau khi tăng cạnh của hình vuông là `C_{s}4 \times(3 \times a)=12 \times a` `(2)`
Từ `(1);(2)=>` Chu vi tăng `12 l`
`->D`

Ngày thứ ba đắp được số m đường là:
100 x 2= 200 ( m)
Trung bình mỗi ngày đội đó đắp được số m đường là:
( 150 + 100 + 200) : 3 = 150 ( m)
Đáp số:................
Ngày thứ 3 đắp được : 100 x 2 = 200 ( m )
Trung bình mỗi ngày đội đắp được là ;
( 150 + 200 + 100 ) : 3 =150 (m )

\(T=\dfrac{\sqrt{\sqrt{5}+2}+\sqrt{\sqrt{5}-2}}{\sqrt{\sqrt{5}+1}}-\sqrt{\left(\sqrt{2}-1\right)^2}\)
\(=\dfrac{\sqrt{\left(\sqrt{5}+2\right)\left(\sqrt{5}+1\right)}+\sqrt{\left(\sqrt{5}-2\right)\left(\sqrt{5}+1\right)}}{\sqrt{5}+1}-\sqrt{2}+1\)
\(=\dfrac{\sqrt{7+3\sqrt{5}}+\sqrt{3-\sqrt{5}}}{\sqrt{5}+1}-\sqrt{2}+1\)
\(\sqrt{2}T=\dfrac{\sqrt{14+6\sqrt{5}}+\sqrt{6-2\sqrt{5}}}{\sqrt{5}+1}-2+\sqrt{2}\)
\(=\dfrac{\sqrt{\left(3+\sqrt{5}\right)^2}+\sqrt{\left(\sqrt{5}-1\right)^2}}{\sqrt{5}+1}-2+\sqrt{2}\)
\(=\dfrac{2+2\sqrt{5}}{\sqrt{5}+1}-2+\sqrt{2}=\sqrt{2}\Rightarrow T=\dfrac{\sqrt{2}}{\sqrt{2}}=1\)
\(T=\dfrac{\sqrt{\sqrt{5}+2}+\sqrt{\sqrt{5}-2}}{\sqrt{\sqrt{5}+1}}-\sqrt{3-2\sqrt{2}}\)
\(=\dfrac{\sqrt{\left(\sqrt{\sqrt{5}+2}+\sqrt{\sqrt{5}-2}\right)^2}}{\sqrt{\sqrt{5}+1}}-\sqrt{\left(\sqrt{2}-1\right)^2}\)
\(=\dfrac{\sqrt{\sqrt{5}+2+2\sqrt{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)+\sqrt{5}-2}}}{\sqrt{\sqrt{5}+1}}-\sqrt{2}+1\)
\(=\dfrac{\sqrt{2\sqrt{5}+2\sqrt{5-4}}}{\sqrt{\sqrt{5}+1}}-\sqrt{2}+1\)
\(=\dfrac{\sqrt{2\sqrt{5}+2}}{\sqrt{\sqrt{5}+1}}-\sqrt{2}+1\)
\(=\dfrac{\sqrt{2}.\sqrt{\sqrt{5}+1}}{\sqrt{\sqrt{5}+1}}-\sqrt{2}+1\)
\(=\sqrt{2}-\sqrt{2}+1=1\)

\(\dfrac{x}{5}=\dfrac{x+2}{7}\\ =>7x=5\left(x+2\right)\\ =>7x=5x+10\\ =>7x-5x=10\\ =>2x=10\\ =>x=5\)
\(\Rightarrow7x=5x+10\Leftrightarrow2x=10\Leftrightarrow x=5\)

Có 3 người trong bữa cơm: một bà , một người mẹ, một đứa con

pp ẩn dụ thì mk ko bt chỉ bt đặt ẩn phụ thôi mà chỗ kia là đấu + ms đúng
\(\left(x^2+x+2\right)^4-3x^2.\left(x^2+x+2\right)^2+2x^4\)
đặt \(\left(x^2+x+2\right)^2=a\left(a>0\right)\)và \(x^2=b\)
\(=a^2-3ab+2b^2\)
\(=\left(a-b\right).\left(a-2b\right)\)
\(=\left[\left(x^2+x+2\right)^2-x^2\right].\left[\left(x^2+x+2\right)^2-2x^2\right]\)
bạn tự pt nốt nhé
Sửa đề: \(A=\left(x^2+x+2\right)^4-3x^2\left(x^2+x+2\right)^2+2x^4\)
- Đặt \(\left\{{}\begin{matrix}\left(x^2+x+2\right)^2=a\\x^2=b\end{matrix}\right.\)
\(\Rightarrow A=a^2-3ab+2b^2=a^2-ab-2ab+2b^2=a\left(a-b\right)-2b\left(a-b\right)=\left(a-b\right)\left(a-2b\right)\)
\(\Rightarrow A=\left[\left(x^2+x+2\right)^2-x^2\right]\left[\left(x^2+x+2\right)^2-2x^2\right]\)
\(=\left(x^2+2\right)\left(x^2+2x+2\right)\left(x^2+x-x\sqrt{2}+2\right)\left(x^2+x+x\sqrt{2}+2\right)\)

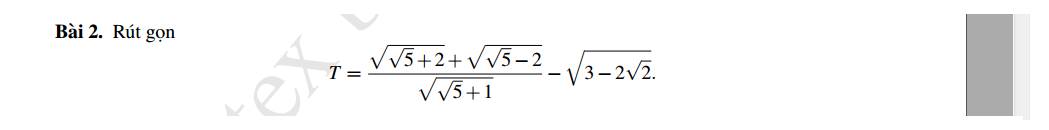
\(\dfrac{3}{1^2x2^2}+\dfrac{5}{2^2x3^2}+\dfrac{7}{3^2x4^2}+...+\dfrac{19}{9^2x10^2}\\ =\dfrac{2^2}{1^2x2^2}-\dfrac{1^2}{1^2x2^2}+\dfrac{3^2}{2^2x3^2}-\dfrac{2^2}{2^2x3^2}+\dfrac{4^2}{3^2x4^2}-\dfrac{3^2}{3^2x4^2}+...+\dfrac{10^2}{9^2x10^2}-\dfrac{9^2}{9^2x10^2}\\ =\dfrac{1}{1^2}-\dfrac{1}{2^2}+\dfrac{1}{2^2}-\dfrac{1}{3^2}+\dfrac{1}{3^2}-\dfrac{1}{4^2}+...+\dfrac{1}{9^2}-\dfrac{1}{10^2}\\ =1-\dfrac{1}{10^2}< 1\\ =>DPCM\)
helppppp