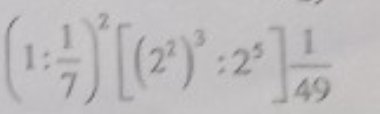
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)5x+17-(2x+5)=0
=>5x+17-2x-5=0
=>3x+12=0
=>3x=-12
=>x=-12:3=-4
b)3(1-x)-(5-2x)=0
=>3-3x-5+2x=0
=>-2-x=0
=>x=-2
c)2(x-1)-3(x-2)=0
=>2x-2-3x+6=0
=>-x+4=0
=>x=4
d)(x-3)(2x-5)+(2x-4)(5-2x)=0
=>(x-3)(2x-5)-(2x-4)(2x-5)=0
=>(2x-5)(x-3-2x+4)=0
=>(2x-5)(1-x)=0
TH1: 2x - 5=0=>2x=5=>x=5/2
TH2: 1-x=0=>x=1
a: Đặt 5x+17-(2x+5)=0
=>\(5x+17-2x-5=0\)
=>\(3x+12=0\)
=>\(3x=-12\)
=>\(x=-\dfrac{12}{3}=-4\)
b: Đặt \(3\left(1-x\right)-\left(5-2x\right)=0\)
=>\(3-3x-5+2x=0\)
=>\(-x-2=0\)
=>x+2=0
=>x=-2
c: Đặt \(2\left(x-1\right)-3\left(x-2\right)=0\)
=>\(2x-2-3x+6=0\)
=>4-x=0
=>x=4
d: Sửa đề: (x-3)(2x-5)+(2x-4)*(5-x)
Đặt \(\left(x-3\right)\left(2x-5\right)+\left(2x-4\right)\left(5-x\right)=0\)
=>\(2x^2-5x-6x+15+10x-2x^2-20+4x=0\)
=>3x-5=0
=>3x=5
=>\(x=\dfrac{5}{3}\)

Đặt 5x+17-(2x+5)=0
=>5x+17-2x-5=0
=>3x+12=0
=>3x=-12
=>\(x=-\dfrac{12}{3}=-4\)

Diện tích xung quanh của căn phòng là:
\(\left(8+6\right)\times2\times4=8\times14=112\left(m^2\right)\)
Diện tích trần nhà là \(8\times6=48\left(m^2\right)\)
Diện tích cửa ra vào là 1x2,2=2,2(m2)
Diện tích 4 cửa số hình vuông là:
4x0,8x0,8=0,64x4=2,56(m2)
Diện tích cần quét vôi là:
112+48-2,2-2,56=155,24(m2)
Diện tích của tất cả cửa là:
\(1\times2,2+4\times0,8\times0,8=4,76\left(m^2\right)\)
Diện tích xung quanh và trần nhà là::
\(2\times4\times\left(8+6\right)+6\times8=160\left(m^2\right)\)
Diện tich cần quét vôi là:
\(160-4,76=155,24\left(m^2\right)\)

Đổi: 8 phút = \(\dfrac{2}{15}\left(h\right)\)
Vận tốc của xe đạp là:
\(1,6:\dfrac{2}{15}=12\left(km/h\right)\)
1,6km=1600m
Vận tốc của xe đạp là 1600:8=200(m/p)=12km/h
=>Chọn C

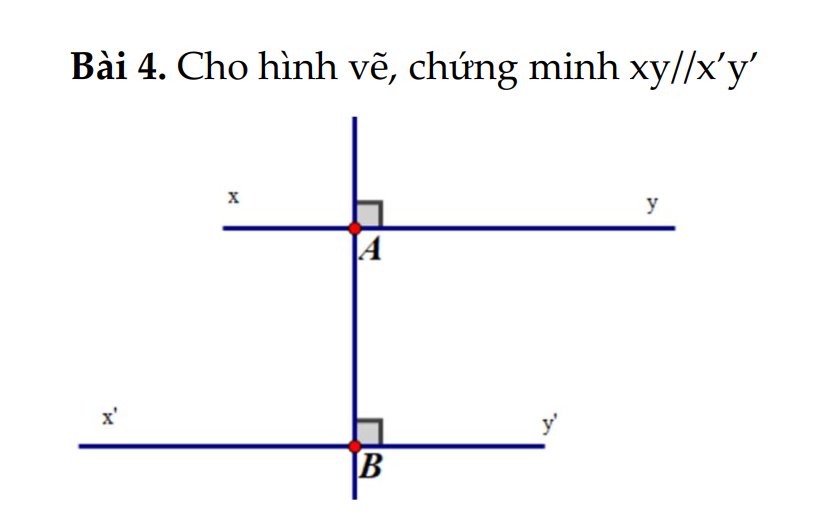
1: Sửa đề: Vẽ \(\widehat{x'Ay'}\) là góc đối đỉnh của góc xAy
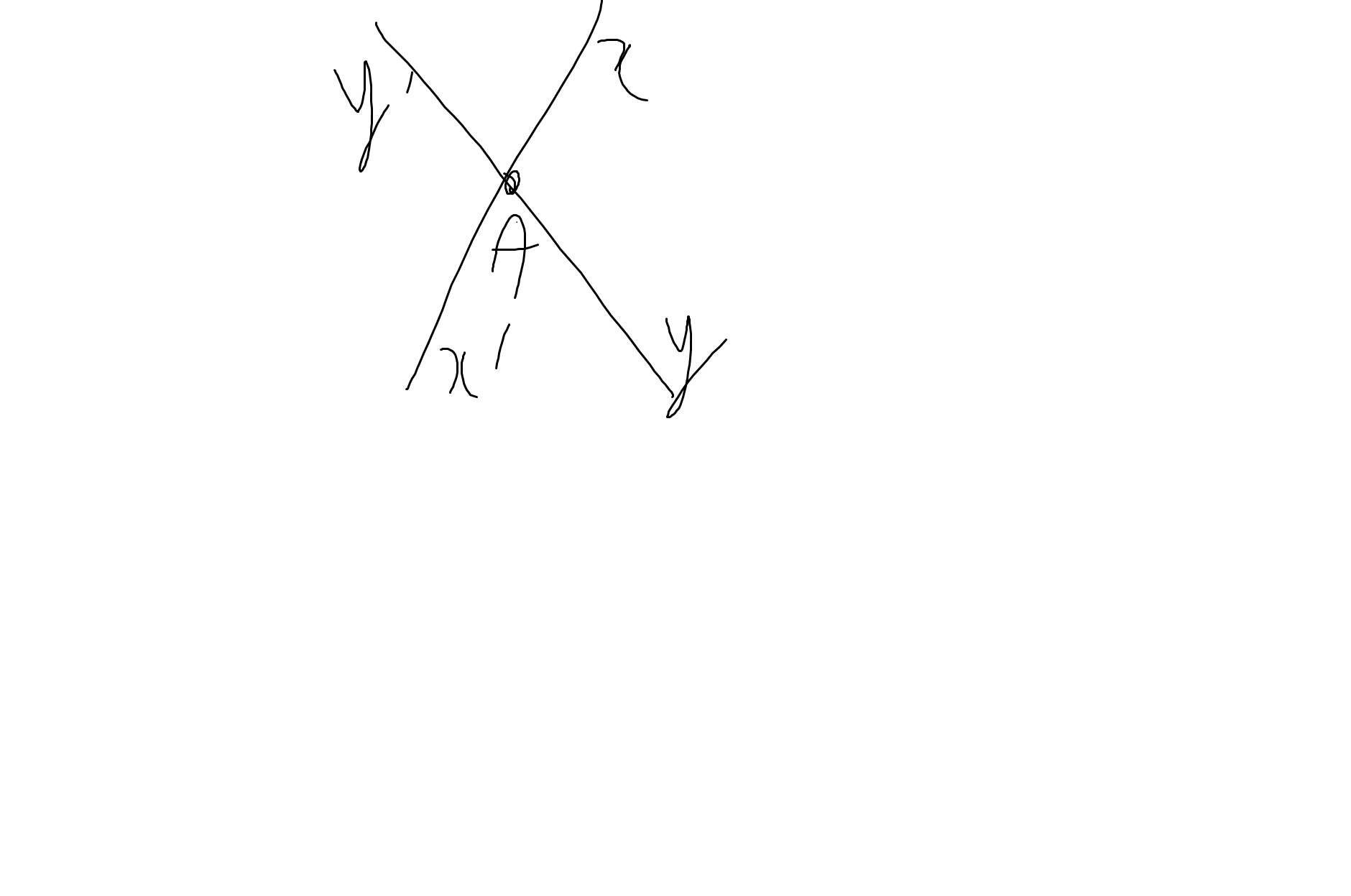
2: Ta có: \(\widehat{xAy}+\widehat{xAy'}=180^0\)(hai góc kề bù)
=>\(\widehat{xAy'}+100^0=180^0\)
=>\(\widehat{xAy'}=80^0\)
Ta có: \(\widehat{xAy}=\widehat{x'Ay'}\)(hai góc đối đỉnh)
mà \(\widehat{xAy}=100^0\)
nên \(\widehat{x'A'y}=100^0\)
Ta có: \(\widehat{xAy'}=\widehat{x'Ay}\)(hai góc đối đỉnh)
mà \(\widehat{xAy'}=80^0\)
nên \(\widehat{x'Ay}=80^0\)

\(\left[\left(\dfrac{4}{3}\right)^{-3}\cdot\left(\dfrac{3}{4}\right)^5\right]:\left(\dfrac{3}{8}\right)^7\\ =\left[\left(\dfrac{3}{4}\right)^3\cdot\left(\dfrac{3}{4}\right)^5\right]:\left(\dfrac{3}{8}\right)^7\\ =\left(\dfrac{3}{4}\right)^{3+5}:\dfrac{3^7}{8^7}\\ =\left(\dfrac{3}{4}\right)^8\cdot\dfrac{8^7}{3^7}\\ =\dfrac{3^8}{4^8}\cdot\dfrac{8^7}{3^7}\\ =\dfrac{3^8}{2^{16}}\cdot\dfrac{2^{21}}{3^7}=3\cdot2^5=3\cdot32=96\)
\(\left[\left(\dfrac{4}{3}\right)^{-3}\cdot\left(\dfrac{3}{4}\right)^5\right]:\left(\dfrac{3}{8}\right)^7\)
\(=\left[\left(\dfrac{3}{4}\right)^3\cdot\left(\dfrac{3}{4}\right)^5\right]:\dfrac{3^7}{8^7}\)
\(=\left(\dfrac{3}{4}\right)^8\cdot\dfrac{8^7}{3^7}=\dfrac{3^8}{4^8}\cdot\dfrac{8^7}{3^7}=\dfrac{3\cdot2^{21}}{2^{16}}=3\cdot2^5=3\cdot32=96\)

a: \(\left\{{}\begin{matrix}x+3y=11\\3x-y=9-2y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+3y=11\\3x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+3y=11\\9x+3y=27\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x+3y-x-3y=27-11\\x+3y=11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x=16\\3y=11-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{11-x}{3}=\dfrac{11-2}{3}=\dfrac{9}{3}=3\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}5\left(x+2y\right)=3x-1\\2x+4=3\left(x-5y\right)-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+10y-3x=-1\\2x+4-3x+15y=-12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+10y=-1\\-x+15y=-16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\-2x+30y=-32\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+10y-2x+30y=-1+\left(-32\right)\\x-15y=16\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}40y=-33\\x=15y+16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{33}{40}\\x=15\cdot\dfrac{-33}{40}+16=\dfrac{29}{8}\end{matrix}\right.\)
a)
\(\left\{{}\begin{matrix}x+3y=11\\3x-y=9-2y\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+3y=11\\3x+y=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3x+9y=33\\3x+y=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}8y=24\\3x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\3x+3=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3\\x=\dfrac{6}{3}=2\end{matrix}\right.\)
b)
\(\left\{{}\begin{matrix}5\left(x+2y\right)=3x-1\\2x+4=3\left(x-5y\right)-12\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x+10y=3x-1\\2x+4=3x-15y-12\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\x-15y=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\2x-30y=32\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}40y=-33\\x-15y=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{33}{40}\\x+\dfrac{99}{8}=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{33}{40}\\x=16-\dfrac{99}{8}=\dfrac{29}{8}\end{matrix}\right.\)

Số có 8 chữ số sẽ có dạng là \(\overline{abcdefgh}\)
chữ số hàng trăm nghìn là 3
=>c=3
Chữ số hàng nghìn là 6
=>e=6
Chữ số hàng chục là 5
=>g=5
=>Số cần tìm có dạng là \(\overline{ab3d6f5h}\)
=>Số lớn nhất sẽ là 99396959
Để số cần tìm lớn nhất có thể thì các chữ số phải là chữ số lớn nhất (số 9) trừ các chữ số đã cho trước.
Số cần tìm là: 99396959
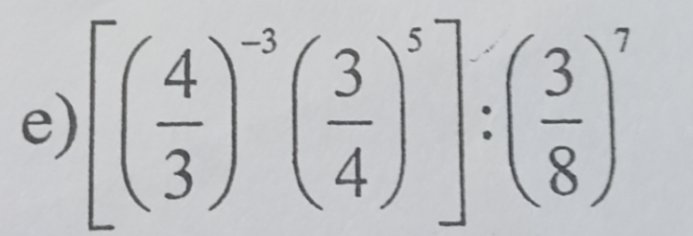
\(\left(1:\dfrac{1}{7}\right)^2\left[\left(2^2\right)^3:2^5\right]\cdot\dfrac{1}{49}\\ =7^2\left(2^6:2^5\right)\cdot\dfrac{1}{7^2}\\=\left(7^2\cdot\dfrac{1}{7^2}\right)\cdot2^{6-5}\\ =1\cdot2^1\\ =2\)
\(\left(1:\dfrac{1}{7}\right)^2\left[\left(2^2\right)^3:2^5\right]\cdot\dfrac{1}{49}\)
\(=\dfrac{7^2}{49}\cdot\left(2^6:2^5\right)\)
\(=\dfrac{49}{49}\cdot2=2\)