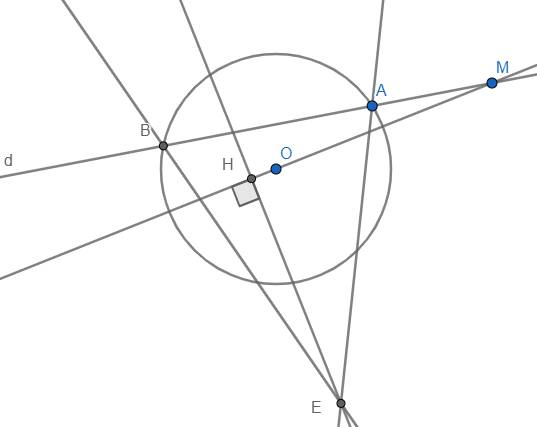
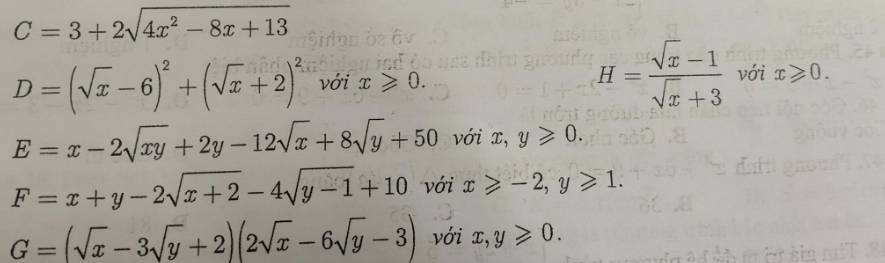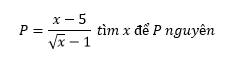cho đường tròn (O;R) và điểm M cố định nằm ngoài đường tròn. một đường thẳng d đi qua M cắt đường tròn (O)tại điểm A và B (MA< MB , d không đi qua tâm O ). Các tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại điểm E. gọi H là chân đường vuông góc kẻ từ điểm E đến OM. vẽ hình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số than đội xe phải chở mỗi ngày theo kế hoạch là x (tấn)
Thời gian chở hết than theo kế hoạch là: \(\dfrac{120}{x}\) ngày
Thực tế mỗi ngày đội chở được: \(x+6\) tấn
Thực tế số than đội chở được là: \(120+10=130\) (tấn)
Thực tế thời gian chở hết số than là: \(\dfrac{130}{x+6}\) ngày
Do đội hoàn thành trước kế hoạch 1 ngày nên ta có pt:
\(\dfrac{120}{x}-\dfrac{130}{x+6}=1\)
\(\Rightarrow120\left(x+6\right)-130x=x\left(x+6\right)\)
\(\Leftrightarrow x^2+16x-720=0\Rightarrow\left[{}\begin{matrix}x=20\\x=-36\left(loại\right)\end{matrix}\right.\)

\(C=3+2\sqrt{4x^2-8x+13}\)
\(=3+2\sqrt{4x^2-8x+4+9}\)
\(=3+2\sqrt{\left(2x-2\right)^2+9}>=3+2\cdot\sqrt{9}=9\)
Dấu '=' xảy ra khi 2x-2=0
=>x=1
\(D=\left(\sqrt{x}-6\right)^2+\left(\sqrt{x}+2\right)^2\)
\(=x-12\sqrt{x}+36+x+4\sqrt{x}+4\)
\(=2x-8\sqrt{x}+40\)
\(=2\left(x-4\sqrt{x}+20\right)\)
\(=2\left(x-4\sqrt{x}+4+16\right)\)
\(=2\left(\sqrt{x}-2\right)^2+32>=32\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\sqrt{x}-2=0\)
=>x=4
\(F=x+y-2\sqrt{x+2}-4\sqrt{y-1}+10\)
\(=x+2-2\sqrt{x+2}+1+y-1-4\sqrt{y-1}+4+4\)
\(=\left(\sqrt{x+2}-1\right)^2+\left(\sqrt{y-1}-2\right)^2+4>=4\forall x,y\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x+2=1\\y-1=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=5\end{matrix}\right.\)

(d')//(d)
=>\(\left\{{}\begin{matrix}a=-1\\b\ne-2\end{matrix}\right.\)
vậy: (d'): y=-x+b
Thay x=-1 và y=3 vào (d'), ta được:
b+1=3
=>b=2(nhận)
vậy: y=-x+2

a: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>CA\(\perp\)SB tại A
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>BD\(\perp\)SC tại D
Xét ΔSBC có
BD,CA là các đường cao
BD cắt CA tại H
Do đó: H là trực tâm của ΔSBC
=>SH\(\perp\)BC tại E
Xét tứ giác HECD có \(\widehat{HDC}+\widehat{HEC}=90^0+90^0=180^0\)
nên HECD là tứ giác nội tiếp
b: ΔSAH vuông tại A
mà AT là đường trung tuyến
nên TA=TH
=>ΔTHA cân tại T
=>\(\widehat{TAH}=\widehat{THA}\)
mà \(\widehat{THA}=\widehat{EHC}\)(hai góc đối đỉnh)
và \(\widehat{EHC}=\widehat{EDC}\)(HDCE nội tiếp)
nên \(\widehat{TAH}=\widehat{KDC}\)

Gọi A là giao điểm của (d') và Ox, tọa độ A là nghiệm:
\(\left\{{}\begin{matrix}y=2x-1\\y=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2x-1=0\\y=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=0\end{matrix}\right.\)
\(\Rightarrow A\left(\dfrac{1}{2};0\right)\)
Để (d) cắt (d') tại 1 điểm trên trục hoành \(\Rightarrow A\) thuộc (d)
Thay tọa độ A vào pt (d) ta được:
\(\dfrac{1}{2}.\left(2m-1\right)+3=0\)
\(\Rightarrow2m+5=0\Rightarrow m=-\dfrac{5}{2}\)

\(P=\dfrac{x-1-4}{\sqrt{x}-1}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)-4}{\sqrt{x}-1}=\sqrt{x}+1-\dfrac{4}{\sqrt{x}-1}\)
P nguyên \(\Rightarrow\dfrac{4}{\sqrt{x}-1}\) nguyên \(\Rightarrow\sqrt{x}-1=Ư\left(4\right)\)
Mà \(\sqrt{x}-1\ge-1;\forall x\)
\(\Rightarrow\sqrt{x}-1=\left\{-1;1;2;4\right\}\)
\(\Rightarrow\sqrt{x}=\left\{0;2;3;5\right\}\)
\(\Rightarrow x=\left\{0;4;9;25\right\}\)


Anh ơi,anh đã có ai nhận được rồi nhé. Em xin nghỉ được vào cao điểm của bạn chưa mình đi.