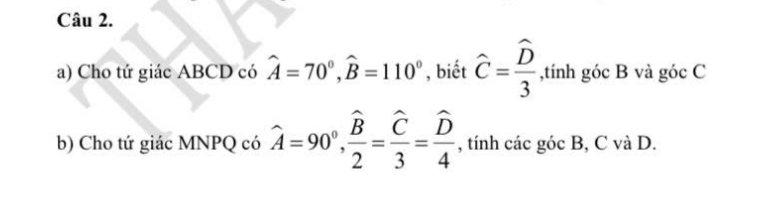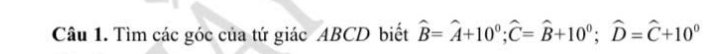`  25.x:17-6=19`

`=>   25.x:17 =19 + 6`

`=>   25.x:17= 25`

`=> 25.x = 25.17`

`=> x =25 . 17 : 25`

`=> x = 17`

Vậy `x = 17`

``
` 2021-10.(x-5)=2021`

`=> 10.(x-5) = 2021 - 2021`

`=> 10 (x-5) = 0`

`=> x - 5 = 0 : 10`

`=> x - 5 = 0`

`=> x = 0+5`

`=> x = 5`

Vậy `x = 5`

\(25x:17-6=19\)

\(25x:17=19+6\)

\(25x:17=25\)

\(x:17=25:25\)

\(x:17=1\)

\(x=1.17\)

\(x=17\)

Vậy `x = 17`

\(2021-10.\left(x-5\right)=2021\)

\(10.\left(x-5\right)=2021-2021\)

\(10.\left(x-5\right)=0\)

\(x-5=0:10\)

\(x-5=0\)

\(x=0+5\)

\(x=5\)

Vậy `x = 5`

a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)

=>\(\widehat{C}+\widehat{D}=360^0-110^0-70^0=180^0\)

=>\(\dfrac{1}{3}\cdot\widehat{D}+\widehat{D}=180^0\)

=>\(\dfrac{4}{3}\cdot\widehat{D}=180^0\)

=>\(\widehat{D}=135^0\)

\(\widehat{C}=\dfrac{1}{3}\cdot135^0=45^0\)

b:

Sửa đề: Cho tứ giác ABCD.

Đặt \(\widehat{B}=x;\widehat{C}=y;\widehat{D}=z\)

\(\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}\)

=>\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\)

Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)

=>\(x+y+z=360^0-90^0=270^0\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{270}{9}=30^0\)

=>\(x=2\cdot30^0=60^0;y=3\cdot30^0=90^0;z=4\cdot30^0=120^0\)

Vậy: \(\widehat{B}=x=60^0;\widehat{C}=y=90^0;\widehat{D}=z=120^0\)

a: \(x=\left(x^3\right)^{\dfrac{1}{3}}\)

b: \(x=\left(x^5\right)^{\dfrac{1}{5}}\)

\(\dfrac{1}{3^6}=\dfrac{1}{3^4\cdot3^2}=\dfrac{1}{81\cdot9}=\dfrac{1}{729}\)

  \(\dfrac{1}{3^6}\) = \(\dfrac{1}{3^4.3^2}\) = \(\dfrac{1}{81.9}\) = \(\dfrac{1}{729}\) 

\(\widehat{C}=\widehat{B}+10^0=\widehat{A}+10^0+10^0=\widehat{A}+20^0\)

\(\widehat{D}=\widehat{C}+10^0=\widehat{A}+20^0+10^0=\widehat{A}+30^0\)

Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)

=>\(\widehat{A}+\widehat{A}+10^0+\widehat{A}+20^0+\widehat{A}+30^0=360^0\)

=>\(4\cdot\widehat{A}=300^0\)

=>\(\widehat{A}=75^0\)

\(\widehat{B}=75^0+10^0=85^0\)

\(\widehat{C}=75^0+20^0=95^0\)

\(\widehat{D}=75^0+30^0=105^0\)

Chưa rõ cụ thể em hỏi cái gì?

nhờ mn giúp mình viết 1 dãy gồm 10000 số pi với ạ mình cảm ơn

Ngày thứ hai bán được số ki-lô-gam là:

\(748\times\dfrac{1}{4}=187\left(kg\right)\)

Tổng số ki-lô-gam của ngày `1` và ngày `2` là:

`748 + 187 = 935 (kg)`

Ngày thứ ba bán được số ki-lô-gam là:

`1080 - 935 = 145 (kg)`

Đáp số : ...

P/S: Sai nói luôn

giải:

Ngày thứ hai bán được số kg đường là:

          748x \(\dfrac{1}{4}\)=187 (kg)

Ngày thứ ba bán được số kg đường là:

          1080 - (748+187)= 145 (kg)

                                      Đ/s:

a: \(\dfrac{\left(-1\right)^2}{2^2}=\dfrac{1}{4};\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)

Do đó: \(\dfrac{\left(-1\right)^2}{2^2}=\left(-\dfrac{1}{2}\right)^2\)

b: \(\dfrac{3^3}{5^3}=\left(\dfrac{3}{5}\right)^3< \dfrac{3}{5}\)(do \(0< \dfrac{3}{5}< 1\))

d: \(\left(\dfrac{3}{4}\right)^7:\left(\dfrac{3}{4}\right)^3=\left(\dfrac{3}{4}\right)^4\)

Vì \(0< \dfrac{3}{4}< 1\)

nên \(\left(\dfrac{3}{4}\right)^4< \left(\dfrac{3}{4}\right)^2\)

=>\(\left(\dfrac{3}{4}\right)^7:\left(\dfrac{3}{4}\right)^3< \left(\dfrac{3}{4}\right)^2\)

e: \(\left(0,5\right)^6:\left(0,5\right)^2=\left(0,5\right)^{6-2}=\left(0,5\right)^4=\left(0,5\right)^{2\cdot2}=\left[\left(0,5\right)^2\right]^2\)

cíu với

\(\left(x+y\right)^2-2\left(x+y\right)+1\)

\(=\left(x+y-1\right)^2\) (HĐT số 2)