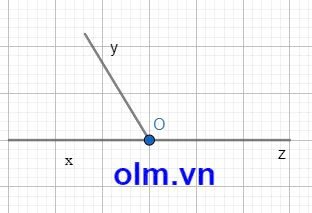
Cho góc xoy kề bù với góc yoz
a)Vẽ hình
b)Vẽ ot,om lần lượt là các tia phân giác của góc xoz,góc yoz.Tính số đo góc tom.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^2y-5y-8x-1=0\)
\(\Leftrightarrow y\left(x^2-5\right)=8x+1\)
\(\Rightarrow y=\dfrac{8x+1}{x^2-5}\) (1)
y nguyên \(\Rightarrow\dfrac{8x+1}{x^2-5}\) nguyên
\(\Rightarrow8x+1⋮x^2-5\)
\(\Rightarrow x\left(8x+1\right)⋮x^2-5\)
\(\Rightarrow8\left(x^2-5\right)+x+40⋮x^2-5\)
\(\Rightarrow x+40⋮x^2-5\)
\(\Rightarrow8\left(x+40\right)-\left(8x+1\right)⋮x^2-5\)
\(\Rightarrow329⋮x^2-5\)
\(\Rightarrow x^2-5\inƯ\left(329\right)\)
Mà \(x^2-5\ge-5;\forall x\)
\(\Rightarrow x^2-5\in\left\{-1;1;11;29;319\right\}\)
\(\Rightarrow x^2\in\left\{4;6;16;34;324\right\}\)
\(\Rightarrow x^2\in\left\{4;16;324\right\}\) do \(x^2\) là SCP
\(\Rightarrow x\in\left\{-18;-4;-2;2;4;18\right\}\)
Thay lần lượt vào (1) ta được: \(\left(x;y\right)=\left(-2;15\right);\left(2;-17\right);\left(4;3\right)\)

\(F=-1-\dfrac{1}{3}-\dfrac{1}{6}-...-\dfrac{1}{1225}\)
\(=-2\left(\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{2450}\right)\)
\(=-2\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}\right)\)
\(=-2\left(1-\dfrac{1}{50}\right)=-2\cdot\dfrac{49}{50}=-\dfrac{49}{25}\)

Để giải hệ phương trình này, chúng ta có thể sử dụng phương pháp giải hệ phương trình bằng cách loại bỏ biến một cách tuần tự. Dưới đây là cách giải:
Từ phương trình thứ nhất: (xy + 2y = 4x + 6) Ta có thể viết lại thành: (2y + xy = 4x + 6) (y(2 + x) = 4x + 6) (y = \frac{4x + 6}{2 + x})
Từ phương trình thứ hai: (yz + 4z = 6y) Ta có thể viết lại thành: (4z + yz = 6y) (z(4 + y) = 6y) (z = \frac{6y}{4 + y})
Từ phương trình thứ ba: (zx + 6x = 2z) Ta có thể viết lại thành: (6x + zx = 2z) (x(6 + z) = 2z) (x = \frac{2z}{6 + z})
Substitute (y) từ phương trình thứ nhất vào phương trình thứ ba, ta được: (y = \frac{4(\frac{2z}{6 + z}) + 6}{2 + \frac{2z}{6 + z}})
Substitute (z) từ phương trình thứ hai vào phương trình thứ ba, ta được: (x = \frac{2(\frac{6(\frac{6y}{4 + y})}{4 + (\frac{6y}{4 + y})})}{6 + \frac{6y}{4 + y}})
Từ đó, chúng ta có thể tìm ra giá trị cụ thể của (x), (y), (z).

\(=\left(2x^3-6x^2\right)+\left(5x^2-15x\right)+\left(2x-6\right)\)
\(=2x^2\left(x-3\right)+5x\left(x-3\right)+2\left(x-3\right)\)
\(=\left(x-3\right)\left(2x^2+5x+2\right)\)
\(=\left(x-3\right)\left(2x^2+4x+x+2\right)\)
\(=\left(x-3\right)\left[2x\left(x+2\right)+\left(x+2\right)\right]\)
\(=\left(x-3\right)\left(x+2\right)\left(2x+1\right)\)

Lời giải:
a. $A(x) = 6x^3-7x^2-x+m=3x^2(2x+1)-5x(2x+1)+2(2x+1)+m-2$
$=(2x+1)(3x^2-5x+2)+m-2$
$=B(x)(3x^2-5x+2)+m-2$
Vậy $A(x):B(x)$ được thương $3x^2-5x+2$ và dư $m-2$
b.
Để dư bằng 4 thì $m-2=4$
$\Leftrightarrow x=6$
a: \(\dfrac{A\left(x\right)}{B\left(x\right)}=\dfrac{6x^3-7x^2-x+m}{2x+1}\)
\(=\dfrac{6x^3+3x^2-10x^2-5x+4x+2+m-2}{2x+1}\)
\(=3x^2-5x+2+\dfrac{m-2}{2x+1}\)
b: Để phép chia \(\dfrac{A\left(x\right)}{B\left(x\right)}\) có dư là 4 thì m-2=4
=>m=6


5A:
b: \(47-\dfrac{\left(45\cdot24-5^2\cdot12\right)}{14}\)
\(=47-\dfrac{1080-25\cdot12}{14}\)
\(=47-\dfrac{1080-300}{14}=47-\dfrac{780}{14}=-\dfrac{61}{7}\)
d: \(2345-1000:\left[19-2\left(2\cdot1-18^2\right)\right]\)
\(=2345-1000:\left(19+2\cdot322\right)\)
\(=2345-\dfrac{1000}{19+644}=2345-\dfrac{1000}{663}=\dfrac{1553735}{663}\)
5B:
b: \(50-\left[\left(20-2^3\right)\right]:2+34\)
\(=84-\dfrac{20-8}{2}=84-6=78\)
c: \(20-\left[30-\left(5-1\right)^2\right]:3\)
\(=20-\dfrac{\left[30-4^2\right]}{3}\)
\(=20-\dfrac{14}{3}=\dfrac{46}{3}\)
d: \(205-\left[1200-\left(4^2-23\right)^3\right]:40\)
\(=205-\left[1200-\left(16-23\right)^3\right]:40\)
\(=205-\dfrac{\left[1200-\left(-7\right)^3\right]}{40}\)
\(=205-\dfrac{1200+343}{40}\)
\(=205-38,575=166,425\)

\(\dfrac{49^5+49^7+49^9}{7^{11}+7^{13}+7^{15}+7^{17}+7^{19}+7^{21}}\)
\(=\dfrac{7^{10}+7^{14}+7^{18}}{7^{11}\left(1+7^2\right)+7^{15}\left(1+7^2\right)+7^{19}\left(1+7^2\right)}\)
\(=\dfrac{7^{10}\left(1+7^4+7^8\right)}{7^{11}\left(1+7^2\right)\left(1+7^4+7^8\right)}=\dfrac{1}{7\left(1+7^2\right)}=\dfrac{1}{7\cdot50}=\dfrac{1}{350}\)
a;