cho S = 3 / 10 + 3 / 11 + 3 / 12 + 3 / 13 + 3 / 14 . chứng minh rằng 1 < S <2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{1}{4}+\dfrac{1}{3}:\left(2x-1\right)=-1\\ \dfrac{1}{3}:\left(2x-1\right)=-\dfrac{5}{4}\\ 2x-1=-\dfrac{4}{15}\\ 2x=\dfrac{11}{15}\\ x=\dfrac{11}{30}\)

Bài 3:
a; \(\frac16\) + \(\frac{-5}{6}\)
= \(-\frac46\)
= \(-\frac23\)
b; \(\frac{-2}{17}\) + \(\frac{3}{19}\) + \(\frac{-15}{17}\) + \(\frac{16}{19}\) + \(\frac56\)
= (\(\frac{-2}{17}\) + \(\frac{-15}{17}\)) + (\(\frac{3}{19}\) + \(\frac{16}{19}\)) + \(\frac56\)
= - 1 + 1 + \(\frac56\)
= 0 + \(\frac56\)
= \(\frac56\)

Olm chào em, với dạng này thì cần có hình minh họa em nhé. Cảm ơn em đã đồng hành cùng Olm. Chúc em học tập hiệu quả và vui vẻ cùng Olm.

Giải:
xét mẫu số các phân số lần lượt là: 11; - 119; -1,1; -2,9
-1,1; -2,9 là số thập phân âm.
11 là số nguyên dương
- 119 là số nguyên âm.
Vậy phân số thỏa mãn đề bài là: \(\frac{31}{-119}\)

Bài 1';
a; \(\frac13\) + \(\frac54\) = \(\frac{4}{12}+\frac{15}{12}\) = \(\frac{19}{12}\)
b; 1,6.2\(\frac14\) - 1,6.3\(\frac12\)
= 1,6.(2\(\frac14\) - 3\(\frac12\))
= 1,6.(\(\frac94\) - \(\frac72\))
= 1,6.(\(\frac94\) - \(\frac{14}{4}\))
= 1,6.(- \(\frac54\))
= -2
c; \(\frac{11}{4}\) .(- \(\frac{4}{11}\)) - \(\frac54\) : \(\frac{11}{4}\)
= -1 - \(\frac54\) x \(\frac{4}{11}\)
= - 1 - \(\frac{5}{11}\)
= - \(\frac{16}{11}\)

Gọi A là góc tạo bởi đường thẳng Y bằng -2x + 1 và chục Ox khi đó.
A 90'< a < 180 B. 90'< a
C.a < 90' D. 0' < a < 90'
Giải giúp v ạ

A = \(\frac{1}{50}\) + \(\frac{1}{51}\) + ... + \(\frac{1}{99}\)
Xét dãy số: 50; 51; 52;..;99
Dãy số trên là dãy số cách đều với khoảng cách là:
51 - 50 = 1
Số số hạng của dãy số trên là: (99 - 50) : 1 + 1 = 50 (số hạng)
Vậy A là tổng của 50 phân số.
\(\frac{1}{50}>\frac{1}{51}>\frac{1}{52}>\ldots>\frac{1}{99}\)
Suy ra: A= \(\frac{1}{50}\) + \(\frac{1}{51}\) + ...+ \(\frac{1}{99}\) > \(\frac{1}{99}\) + \(\frac{1}{99}\) + ... + \(\frac{1}{99}\)(50 phân số\(\frac{1}{99}\))
A = \(\frac{1}{50}+\frac{1}{51}+\frac{1}{52}+\cdots+\frac{1}{99}\) > \(\frac{1}{99}\) x 50
A = \(\frac{1}{50}+\frac{1}{51}+\frac{1}{52}+\cdots+\frac{1}{99}\) > \(\frac{50}{99}\) > \(\frac{50}{100}\) = \(\frac12\) (đpcm)

Giải:
a; A = \(\frac{n-7}{n+3}\)
A ∈ Z khi và chi khi:
(n - 7) ⋮ (n + 3)
[(n + 3) - 10] ⋮ (n + 3)
10 ⋮ (n+ 3)
(n + 3) ∈ Ư(10) = {-10; -5; -2; -1; 1; 2; 5; 10}
Lập bảng ta có:
n+3 | -10 | -5 | -2 | -1 | 1 | 2 | 5 | 10 |
n | -13 | -8 | -5 | -4 | -2 | -1 | 2 | 7 |
n∈Z | tm | tm | tm | tm | tm | tm | tm | tm |
Theo bảng trên ta có:
n ∈ {-13; -8; -5; -4; -2; -1; 2; 7}
Vậy n ∈ {-13; -8; -5; -4; -2; -1; 2; 7}
b; B = \(\frac{6n-5}{3n+2}\)
B ∈ Z khi và chỉ khi:
(6n - 5) ⋮ (3n + 2)
[2.(3n + 2) - 9]⋮(3n + 2)
9 ⋮ (3n + 2)
(3n + 2) ∈ Ư(9) = {-9; -3; -1; 1; 3; 9}
Lập bảng giá trị ta có:
3n+2 | -9 | -3 | -1 | 1 | 3 | 9 |
n | -\(\frac{11}{3}\) | -\(\frac53\) | -1 | -\(\frac13\) | \(\frac13\) | \(\frac73\) |
n∈Z | loại | loại | tm | loại | loại | loại |
Theo bảng trên ta có: n = -1
Vậy n = -1
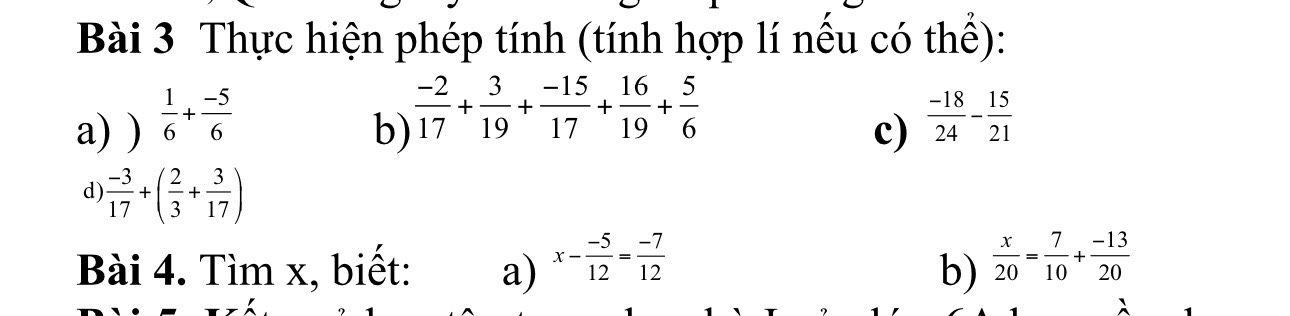
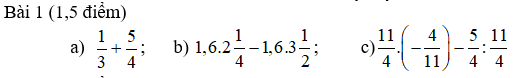
Vì \(\frac{3}{10}>\frac{3}{11}>\frac{3}{12}>\frac{3}{13}>\frac{3}{14}\)
Ta có: \(\frac{3}{14}\) x 5 < \(\frac{3}{10}+\frac{3}{11}<\frac{3}{12}<\frac{3}{13}<\frac{3}{14}\) < \(\frac{3}{10}\) x 5
\(\frac{15}{14}\) < S < \(\frac{15}{10}\)
1\(\frac{1}{14}\) < S < 1\(\frac{5}{10}\)
1 < S < 2 (đpcm)
các bạn trả lời nhiều quá