
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\dfrac{x-1}{4}-\dfrac{3x}{2}=1+\dfrac{2x-1}{3}\)
=>\(\dfrac{x-1-6x}{4}=\dfrac{3+2x-1}{3}\)
=>\(\dfrac{-5x-1}{4}=\dfrac{2x+2}{3}\)
=>\(4\left(2x+2\right)=3\left(-5x-1\right)\)
=>-15x-3=8x+8
=>-23x=11
=>\(x=-\dfrac{11}{23}\)
b: \(\left(4x-1\right)\left(x+5\right)=x^2-25\)
=>\(\left(4x-1\right)\left(x+5\right)-\left(x-5\right)\left(x+5\right)=0\)
=>\(\left(x+5\right)\left(4x-1-x+5\right)=0\)
=>(x+5)(3x+4)=0
=>\(\left[{}\begin{matrix}x=-5\\x=-\dfrac{4}{3}\end{matrix}\right.\)
c: \(x\left(x-1\right)\left(x^2-x+1\right)-6=0\)
=>\(\left(x^2-x\right)\left(x^2-x+1\right)-6=0\)
=>\(\left(x^2-x\right)^2+\left(x^2-x\right)-6=0\)
=>\(\left(x^2-x+3\right)\left(x^2-x-2\right)=0\)
mà \(x^2-x+3=\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\forall x\)
nên \(x^2-x-2=0\)
=>(x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)

a: Thay x=5 vào A, ta được:
\(A=\dfrac{5+3}{5^2}=\dfrac{8}{25}\)
b: \(B=\dfrac{x-6}{x^2-4}+\dfrac{3}{x-2}+\dfrac{x}{x+2}\)
\(=\dfrac{x-6}{\left(x-2\right)\left(x+2\right)}+\dfrac{3}{x-2}+\dfrac{x}{x+2}\)
\(=\dfrac{x-6+3\left(x+2\right)+x\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x-6+3x+6+x^2-2x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+2x}{\left(x-2\right)\left(x+2\right)}=\dfrac{x}{x-2}\)
c: \(P=A\cdot B=\dfrac{x}{x-2}\cdot\dfrac{x+3}{x^2}=\dfrac{x+3}{x\left(x-2\right)}\)
\(P=\dfrac{1}{x+2}\)
=>\(\dfrac{x+3}{x\left(x-2\right)}=\dfrac{1}{x+2}\)
=>\(x\left(x-2\right)=\left(x+3\right)\left(x+2\right)\)
=>\(x^2+5x+6=x^2-2x\)
=>7x=-6
=>\(x=-\dfrac{6}{7}\left(nhận\right)\)

Đây là dạng toán nâng cao chuyên tổng tỉ lồng nhau, cấu trúc thi chuyên, thi viplympic, thi học sinh giỏi các cấp. Hôm nay Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Số khẩu trang ủng hộ đợt 1 là:
12000 x 25% = 3000 (khẩu trang)
Tổng số khẩu trang ủng hộ đợt 2 và đợt 3 là:
12000 - 3000 = 9000 (khẩu trang)
Nếu đợt 2 phân xưởng ủng hộ thêm 250 hộp khẩu trang nữa thì tổng số khẩu trang của đợt 2 và đợt 3 là:
9000 + 250 = 9250 (khẩu trang)
Ta có sơ đồ:
Theo sơ đồ ta có:
Số khẩu trang đợt 3 là:
9250 : (2 + 3) x 3 = 5550 (khẩu trang)
Số khẩu trang đợt 2 là:
12000 - 3000 - 5550 = 3450 (khẩu trang)
Đáp số:...

a: \(3x\left(x-7\right)+2xy-14y\)
\(=3x\left(x-7\right)+2y\left(x-7\right)\)
=(x-7)(3x+2y)
b: \(\left(4x-y\right)\left(a+b\right)-\left(y-4x\right)\left(b-1\right)\)
\(=\left(4x-y\right)\left(a+b\right)+\left(4x-y\right)\left(b-1\right)\)
\(=\left(4x-y\right)\left(a+b+b-1\right)\)
\(=\left(4x-y\right)\left(a+2b-1\right)\)
c: \(2x^2-x-6xy+3y\)
\(=\left(2x^2-x\right)-\left(6xy-3y\right)\)
\(=x\left(2x-1\right)-3y\left(2x-1\right)\)
\(=\left(2x-1\right)\left(x-3y\right)\)
d: \(x^2-z^2+4xy+4y^2\)
\(=\left(x^2+4xy+4y^2\right)-z^2\)
\(=\left(x+2y\right)^2-z^2\)
\(=\left(x+2y+z\right)\left(x+2y-z\right)\)

a: \(\left(2-3x\right)^2-5x\left(x-4\right)+4\left(x-1\right)\)
\(=9x^2-12x+4-5x^2+20x+4x-4\)
\(=4x^2+12x\)
b: \(\left(x-1\right)^2-2\left(x-1\right)\left(x+2\right)+\left(x+2\right)^2+5\left(2x-3\right)\)
\(=x^2-2x+1-2\left(x^2+x-2\right)+x^2+4x+4+10x-15\)
\(=2x^2+12x-14-2x^2-2x+4\)
=10x-10
c: \(\left(x-2\right)^3-6\left(x+4\right)\left(x-4\right)-\left(x-2\right)\left(x^2+2x+4\right)\)
\(=x^3-6x^2+12x-8-\left(x^3-8\right)-6\left(x^2-16\right)\)
\(=x^3-6x^2+12x-8-x^3+8-6x^2+96\)
\(=-12x^2+12x+96\)

Lời giải:
Giả sử đội 1 và đội 2 làm riêng trong lần lượt $a$ và $b$ giờ thì hoàn thành công việc.
Trong 1 giờ: đội 1 làm được $\frac{1}{a}$ công việc, đội 2 làm được $\frac{1}{b}$ công việc.
Theo bài ra ta có:
\(\left\{\begin{matrix}\ \frac{6}{a}+\frac{6}{b}=\frac{11}{15}\\ \frac{5}{a}+\frac{6}{b}=\frac{2}{3}\end{matrix}\right.\Rightarrow \left\{\begin{matrix} \frac{1}{a}=\frac{1}{15}\\ \frac{1}{b}=\frac{1}{18}\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=15\\ b=18\end{matrix}\right.\)

b: Phương trình hoành độ giao điểm là:
\(x^2=x+2\)
=>\(x^2-x-2=0\)
=>(x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Khi x=2 thì \(y=2^2=4\)
Khi x=-1 thì \(y=\left(-1\right)^2=1\)
Vậy: A(-1;1); B(2;4)
C thuộc (P)
=>\(C\left(x;x^2\right)\)
B(2;4); A(-1;1); C(x;x2)
\(\overrightarrow{BA}=\left(-3;-3\right);\overrightarrow{BC}=\left(x-2;x^2-4\right)\)
ΔBAC vuông tại B
=>\(\overrightarrow{BA}\cdot\overrightarrow{BC}=0\)
=>\(-3\left(x-2\right)+\left(-3\right)\left(x^2-4\right)=0\)
=>\(\left(x-2\right)+\left(x^2-4\right)=0\)
=>\(x^2+x-6=0\)
=>(x+3)(x-2)=0
=>\(\left[{}\begin{matrix}x=-3\left(nhận\right)\\x=2\left(loại\right)\end{matrix}\right.\)
Khi x=-3 thì \(y=\left(-3\right)^2=9\)
vậy: C(-3;9); A(-1;1); B(2;4)
\(BA=\sqrt{\left(-1-2\right)^2+\left(1-4\right)^2}=3\sqrt{2}\)
\(BC=\sqrt{\left(-3-2\right)^2+\left(9-4\right)^2}=5\sqrt{2}\)
\(AC=\sqrt{\left(-3+1\right)^2+\left(9-1\right)^2}=2\sqrt{17}\)
Khoảng cách từ B đến AC là:
\(\dfrac{BA\cdot BC}{AC}=\dfrac{3\sqrt{2}\cdot5\sqrt{2}}{2\sqrt{17}}=\dfrac{15}{\sqrt{17}}\)

Gọi số đó là abcd (a;b;c;d đều là chữ số, a khác 0)
Theo bài ra ta có:
abcd chia hết cho cả 2 và 5 ⇒ d=0 ⇒ abcd có dạng abc0
Lại có abc0 = 1638 + abc
⇒ abc x 10 = 1638 + abc
⇒ abc x 10 - abc = 1638
⇒ abc x 9 = 1638
⇒ abc = 1638 : 9
⇒ abc = 182 ⇒ abcd = 1820
Vậy số cần tìm là 1820
Giải:
Vì số cần tìm chia hết cho 2 và 5 nên số cần tìm có chữ số tận cùng là 0
Vì bỏ chữ số tận cùng của số đó đi thì được số mới nên số mới bằng \(\dfrac{1}{10}\) số cần tìm.
Ta có sơ đồ:
Theo sơ đồ ta có: Số cần tìm là: 1638 : (10 - 1) x 10 = 1820
Đáp số: 1820.

Hướng dẫn giải
Bước 1 tìm xem khi đổi chỗ chữ số 8 và chữ số 4 ta được số mới là số nào?
Bước 2: So sánh xem số mới bé hơn hay lớn hơn số ban đầu?
Bước 3 tìm xem số mới hơn hay kém số ban đầu bao nhiêu đơn vi?
Bước 4 kết luận:
Giải:
Số 18540 khi đổi chỗ chữ số 8 và chữ số 4 ta được số mới là: 14580
Vì 18540 > 14580 vậy số 18540 khi đổi chỗ chữ số 8 cho chữ số 4 thì số đó giảm đi và giảm đi số đơn vị là:
18540 - 14580 = 3960 (đơn vị)
Kết luận: Khi thay đổi chữ số 8 và chữ số 4 của số 18 540 thì số đó giảm đi, và giảm đi 3960 đơn vị
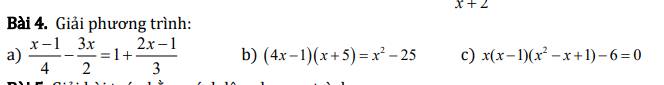


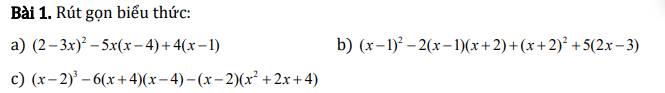
Gọi độ dài quãng đường AB là x(km)
(Điều kiện: x>0)
Thời gian ô tô đi từ A đến B là \(\dfrac{x}{50}\left(giờ\right)\)
Thời gian ô tô đi từ B về A là \(\dfrac{x}{60}\left(giờ\right)\)
Tổng thời gian đi và về là:
4h-20p=3h40p=11/3(giờ)
Do đó, ta có phương trình:
\(\dfrac{x}{50}+\dfrac{x}{60}=\dfrac{11}{3}\)
=>\(\dfrac{11x}{300}=\dfrac{11}{3}\)
=>\(\dfrac{x}{300}=\dfrac{1}{3}\)
=>x=100(nhận)
vậy: Độ dài quãng đường AB là 100km