
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(3\cdot9\cdot\left(-27\right)=3\cdot3^2\cdot\left(-3^3\right)=-3^6\)
b: \(5\cdot25\cdot\left(-125\right)^2=5\cdot5^2\cdot\left(5^3\right)^2=5^9\)
c: \(0,5\cdot\left(-0,25\right)\cdot0,0625=0,5\cdot\left(-1\right)\cdot\left(0,5\right)^2\cdot\left(0,5\right)^4\)
\(=-\left(0,5\right)^7\)
d: \(2\cdot32\cdot\left(-1024\right)=2\cdot2^5\cdot\left(-1\right)\cdot2^{10}=-2^{16}\)
e: \(49\cdot7^3\cdot\left(-7\right)^3=7^2\cdot7^3\cdot\left(-1\right)\cdot7^3=-7^8\)
f: \(\dfrac{3}{4}\cdot\dfrac{9}{16}\cdot\dfrac{27}{64}=\dfrac{3}{4}\cdot\left(\dfrac{3}{4}\right)^2\cdot\left(\dfrac{3}{4}\right)^3=\left(\dfrac{3}{4}\right)^6\)
a, 3.9.27
= - 3.32.33
= - 31+2+3
= - 33+3
= - 36

Bài 3:
a: ĐKXĐ: \(x\ne-1\)
Để A là số nguyên thì \(4⋮x+1\)
=>\(x+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{0;-2;1;-3;3;-5\right\}\)
b: DKXĐ: x<>-1
Để B là số nguyên thì \(x+3⋮x+1\)
=>\(x+1+2⋮x+1\)
=>\(2⋮x+1\)
=>\(x+1\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{0;-2;1;-3\right\}\)
c: ĐKXĐ: x<>2
Để C là số nguyên thì \(x-5⋮x-2\)
=>\(x-2-3⋮x-2\)
=>\(-3⋮x-2\)
=>\(x-2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{3;1;5;-1\right\}\)
d: ĐKXĐ: x<>-1/2
Để D là số nguyên thì \(4x-3⋮2x+1\)
=>\(4x+2-5⋮2x+1\)
=>\(-5⋮2x+1\)
=>\(2x+1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{0;-1;2;-3\right\}\)
Bài 4:
a: ĐKXĐ: \(x\ne0\)
Để \(\dfrac{3}{x}>0\) thì x>0
b: ĐKXĐ: \(x\ne0\)
Để \(\dfrac{4}{3x}>0\) thì 3x>0
=>x>0
c: ĐKXĐ: \(x\ne-1\)
Để \(\dfrac{2}{x+1}>0\) thì x+1>0
=>x>-1
d: ĐKXĐ: \(x\ne2\)
Để \(-\dfrac{1}{x-2}\)>0 thì x-2<0
=>x<2
e: ĐKXĐ: \(x\ne-4\)
Để \(\dfrac{x}{x+4}>0\) thì \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x>0\\x+4>0\end{matrix}\right.\\\left\{{}\begin{matrix}x< 0\\x+4< 0\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x>0\\x< -4\end{matrix}\right.\)

1: \(\dfrac{-2}{3}+\dfrac{3}{4}-\dfrac{-1}{6}+\dfrac{-2}{5}\)
\(=-\dfrac{40}{60}+\dfrac{45}{60}+\dfrac{10}{60}-\dfrac{24}{60}\)
\(=\dfrac{5-14}{60}=-\dfrac{9}{60}=-\dfrac{3}{20}\)
2: \(\dfrac{-2}{3}+\dfrac{-1}{5}+\dfrac{3}{4}-\dfrac{5}{6}-\dfrac{-7}{10}\)
\(=\left(-\dfrac{2}{3}+\dfrac{3}{4}-\dfrac{5}{6}\right)+\left(-\dfrac{1}{5}+\dfrac{7}{10}\right)\)
\(=\left(-\dfrac{8}{12}+\dfrac{9}{12}-\dfrac{10}{12}\right)+\left(-\dfrac{2}{10}+\dfrac{7}{10}\right)\)
\(=\dfrac{-9}{12}+\dfrac{5}{10}=-\dfrac{3}{4}+\dfrac{1}{2}=-\dfrac{3}{4}+\dfrac{2}{4}=-\dfrac{1}{4}\)
3: \(\dfrac{1}{2}-\dfrac{-2}{5}+\dfrac{1}{3}+\dfrac{5}{7}-\dfrac{-1}{6}+\dfrac{-4}{35}+\dfrac{1}{41}\)
\(=\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{6}\right)+\left(\dfrac{2}{5}+\dfrac{5}{7}-\dfrac{4}{35}\right)+\dfrac{1}{41}\)
\(=\dfrac{3+2+1}{6}+\dfrac{14+25-4}{35}+\dfrac{1}{41}\)
\(=\dfrac{6}{6}+\dfrac{35}{35}+\dfrac{1}{41}=2+\dfrac{1}{41}=\dfrac{83}{41}\)
4: \(\dfrac{1}{100\cdot99}-\dfrac{1}{99\cdot98}-\dfrac{1}{98\cdot97}-...-\dfrac{1}{3\cdot2}-\dfrac{1}{2\cdot1}\)
\(=\dfrac{1}{100\cdot99}-\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{97\cdot98}+\dfrac{1}{98\cdot99}\right)\)
\(=\dfrac{1}{100\cdot99}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{98}-\dfrac{1}{99}\right)\)
\(=\dfrac{1}{99}-\dfrac{1}{100}-\dfrac{98}{99}=\dfrac{-97}{99}-\dfrac{1}{100}=\dfrac{-9799}{9900}\)
5: \(\dfrac{\left(\dfrac{3}{10}-\dfrac{4}{15}-\dfrac{7}{20}\right)\cdot\dfrac{5}{19}}{\left(\dfrac{1}{14}+\dfrac{1}{7}-\dfrac{-3}{35}\right)\cdot\dfrac{-4}{3}}=\dfrac{\dfrac{18-16-21}{60}\cdot\dfrac{5}{19}}{\dfrac{5+10+6}{70}\cdot\dfrac{-4}{3}}\)
\(=\dfrac{\dfrac{-19}{60}\cdot\dfrac{5}{19}}{\dfrac{21}{70}\cdot\dfrac{-4}{3}}=\dfrac{-5}{60}:\dfrac{-84}{210}=\dfrac{-1}{12}\cdot\dfrac{-5}{2}=\dfrac{5}{24}\)
6: \(\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{\dfrac{4}{9}-\dfrac{4}{7}-\dfrac{4}{11}}+\dfrac{\dfrac{3}{5}-\dfrac{3}{25}-\dfrac{3}{125}-\dfrac{3}{625}}{\dfrac{4}{5}-\dfrac{4}{25}-\dfrac{4}{125}-\dfrac{4}{625}}\)
\(=\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{4\left(\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}\right)}+\dfrac{3\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}{4\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}\)
\(=\dfrac{1}{4}+\dfrac{3}{4}=\dfrac{4}{4}=1\)

\(D=x^2+y^2-x+6y+10\\ =\left(x^2-x+\dfrac{1}{4}\right)+\left(y^2+6y+9\right)+\dfrac{3}{4}\\ =\left(x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}\right)+\left(y^2+2\cdot y\cdot3+3^2\right)+\dfrac{3}{4}\\ =\left(x-\dfrac{1}{2}\right)^2+\left(y+3\right)^2+\dfrac{3}{4}\)
Ta có: \(\left\{{}\begin{matrix}\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\\\left(y+3\right)^2\ge0\forall y\end{matrix}\right.=>D=\left(x-\dfrac{1}{2}\right)^2+\left(y+3\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x,y\)
Dấu "=" xảy ra \(\left\{{}\begin{matrix}x-\dfrac{1}{2}=0\\y+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-3\end{matrix}\right.\)
______________________________
\(F=2xy-2x^2-y^2+10x-27\\ =-\left(x^2-2xy+y^2\right)-\left(x^2-10x+25\right)-2\\ =-\left(x-y\right)^2-\left(x-5\right)^2-2\)
Ta có: \(\left\{{}\begin{matrix}\left(x-y\right)^2\le0\forall x,y\\-\left(x-5\right)^2\le0\forall x\end{matrix}\right.=>F=-\left(x-y\right)^2-\left(x-5\right)^2-2\le-2\forall x,y\)
Dấu "=" xảy ra: \(\left\{{}\begin{matrix}x-y=0\\x-5=0\end{matrix}\right.\Leftrightarrow x=y=5\)
\(A=-x^2+x-1\)
\(=-\left(x^2-x+1\right)\)
\(=-\left(x^2-x+\dfrac{1}{4}+\dfrac{3}{4}\right)\)
\(=-\left(x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}< =-\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{1}{2}=0\)
=>\(x=\dfrac{1}{2}\)
\(B=6x-x^2-10\)
\(=-\left(x^2-6x+10\right)\)
\(=-\left(x^2-6x+9+1\right)\)
\(=-\left(x-3\right)^2-1< =-1\forall x\)
Dấu '=' xảy ra khi x-3=0
=>x=3
\(C=-x^2+5x+3\)
\(=-\left(x^2-5x-3\right)\)
\(=-\left(x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}-\dfrac{37}{4}\right)\)
\(=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{37}{4}< =\dfrac{37}{4}\forall x\)
Dấu '=' xảy ra khi x-5/2=0
=>x=5/2
\(D=x^2-x+y^2+6y+10\)
\(=x^2-x+\dfrac{1}{4}+y^2+6y+9+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\left(y+3\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-\dfrac{1}{2}=0\\y+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-3\end{matrix}\right.\)
\(F=2xy-2x^2-y^2+10x-27\)
\(=-\left(2x^2+y^2-2xy-10x+27\right)\)
\(=-\left(x^2-2xy+y^2+x^2-10x+25+2\right)\)
\(=-\left(x-y\right)^2-\left(x-5\right)^2-2< =-2\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-y=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=x=5\end{matrix}\right.\)


Gọi mẫu số của phân số cần tìm là x
Theo đề, ta có: \(-\dfrac{11}{13}< \dfrac{9}{x}< \dfrac{-11}{15}\)
=>\(\dfrac{11}{13}>\dfrac{-9}{x}>\dfrac{11}{15}\)
=>\(\dfrac{99}{117}>\dfrac{-99}{11x}>\dfrac{99}{135}\)
=>\(\dfrac{99}{117}>\dfrac{99}{-11x}>\dfrac{99}{135}\)
=>\(-11x\in\left\{118;119;...;134\right\}\)
=>\(x\in\left\{-\dfrac{118}{11};-\dfrac{119}{11};...;\dfrac{134}{-11}\right\}\)
mà x nguyên
nên \(x\in\left\{-11;-12\right\}\)
Vậy: Hai phân số cần tìm là \(\dfrac{9}{-11};\dfrac{9}{-12}\)
=>

\(\dfrac{a}{d}+\dfrac{c}{d}=\dfrac{a}{b}\cdot\dfrac{c}{d}\\ =>\dfrac{a}{b}\cdot\dfrac{c}{d}-\dfrac{c}{d}=\dfrac{a}{b}\\ =>\dfrac{c}{d}\cdot\left(\dfrac{a}{b}-1\right)=\dfrac{a}{b}\\ =>\dfrac{c}{d}\cdot\dfrac{a-b}{b}=\dfrac{a}{b}\\ =>\dfrac{c}{d}=\dfrac{a}{b}:\dfrac{a-b}{b}\\ =>\dfrac{c}{d}=\dfrac{a}{b}\cdot\dfrac{b}{a-b}\\ =>\dfrac{c}{d}=\dfrac{a}{a-b}\)
Vậy: ...

a) Để A là phân số thì \(n-2\ne0\Rightarrow n\ne2\)
b) \(A=-3=>\dfrac{2n-7}{n-2}=-3\)
\(=>2n-7=-3\left(n-2\right)\\ =>2n-7=-3n+6\\ =>2n+3n=6+7\\ =>5n=13\\ =>n=\dfrac{13}{5}\left(ktm\right)\)
c) \(A=\dfrac{2n-7}{n-2}=\dfrac{2n-4-3}{n-2}=\dfrac{2\left(n-2\right)-3}{n-2}=2-\dfrac{3}{n-2}\)
Để A nguyên thì: 3 ⋮ n - 2
=> n - 2 ∈ Ư(3) ={1; -1; 3; -3}
=> n ∈ {3; 1; 5; -1}
d) Để A lớn nhất thì \(\dfrac{3}{n-2}\) nhỏ nhất
=> \(\dfrac{3}{n-2}=-1\)
=> 3 = -(n - 2)
=> 3 = -n + 2
=> n = -1
e) Để A nhỏ nhất thì \(\dfrac{3}{n-2}\) lớn nhất
=> \(\dfrac{3}{n-2}=1\)
=> 3 = n - 2
=> n = 3 + 2
=> n = 5
f) Để A là phân số tối giản => ƯCLN(2n - 7; n - 2) = 1
=> ƯCLN(3; n - 2) = 1
=> n - 2 không chia hết cho 3
=> n - 2 ≠ 3k
=> n ≠ 3k + 2
g) Gọi d là ước nguyên tố của 2n - 7 và n - 2 ta có:
2n - 7 ⋮ d và n - 2 ⋮ d
=> 2n - 7 ⋮ d và 2(n - 2) ⋮ d
=> (2n - 4) - (2n - 7) ⋮ d
=> 3 ⋮ d
=> d ∈ {1; -1; 3; -3}
Mà d là STN => d = 3
Với d = 3 => 2n - 7 ⋮ 3 => 2(2n - 7) ⋮ 3 => 4n - 7 ⋮ 3
=> 3n + n - 7 ⋮ 3
=> n - 7 ⋮ 3
=> n - 7 = 3k
=> n = 3k + 7
bạn cho mình hỏi sao câu d và câu e lại là -1 và 1 thế ạ?

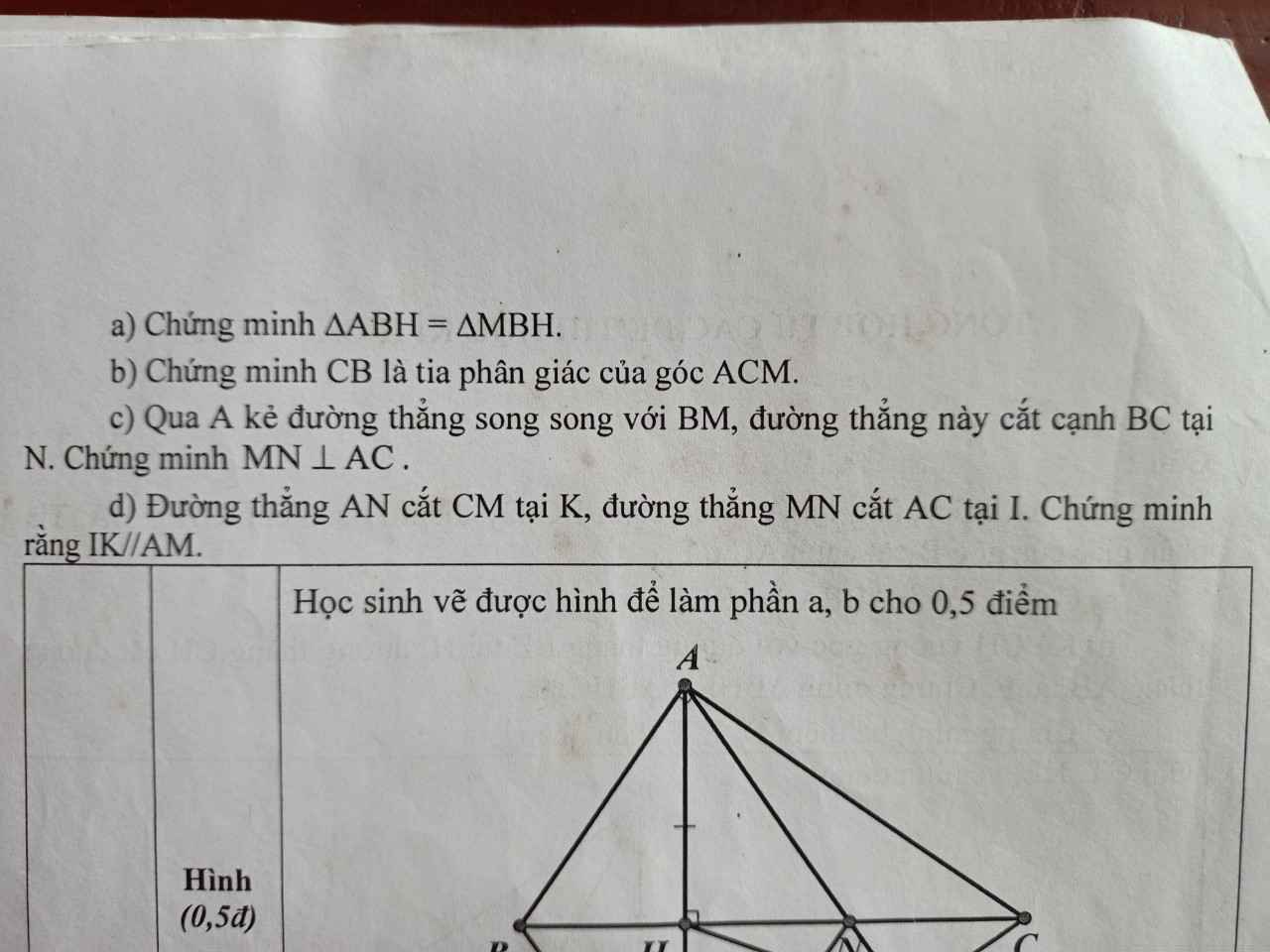
Câu 2:
a: Xét ΔBHA vuông tại H và ΔBHM vuông tại H có
BH chung
HA=HM
Do đó: ΔBHA=ΔBHM
b: ΔBHA=ΔBHM
=>BA=BM và \(\widehat{ABH}=\widehat{MBH}\)
Xét ΔBAC và ΔBMC có
BA=BM
\(\widehat{ABC}=\widehat{MBC}\)
BC chung
Do đó: ΔBAC=ΔBMC
=>\(\widehat{ACB}=\widehat{MCB}\)
=>CB là phân giác của góc ACM
c: ΔBAC=ΔBMC
=>\(\widehat{BAC}=\widehat{BMC}\)
=>\(\widehat{BMC}=90^0\)
Ta có: AN//BM
BM\(\perp\)MC
Do đó: AN\(\perp\)CM
Xét ΔCAM có
CH,AN là các đường cao
CH cắt AN tại N
Do đó: N là trực tâm của ΔCAM
=>MN\(\perp\)AC
d: ΔCAB=ΔCMB
=>CA=CM
=>ΔCAM cân tại C
Xét ΔCKA vuông tại K và ΔCIM vuông tại I có
CA=CM
\(\widehat{ACK}\) chung
Do đó: ΔCKA=ΔCIM
=>CI=CK
Xét ΔCAM có \(\dfrac{CI}{CA}=\dfrac{CK}{CM}\)
nên IK//AM




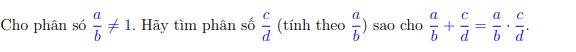
 Help!
Help!
Bài 12:
Thay x=1 vào A(x), ta được:
\(A\left(1\right)=\left(3-4\cdot1+1^2\right)^{2004}\cdot\left(3+4\cdot1+1^2\right)^{2005}=0\)
=>Tổng của tất cả các hệ số là 0