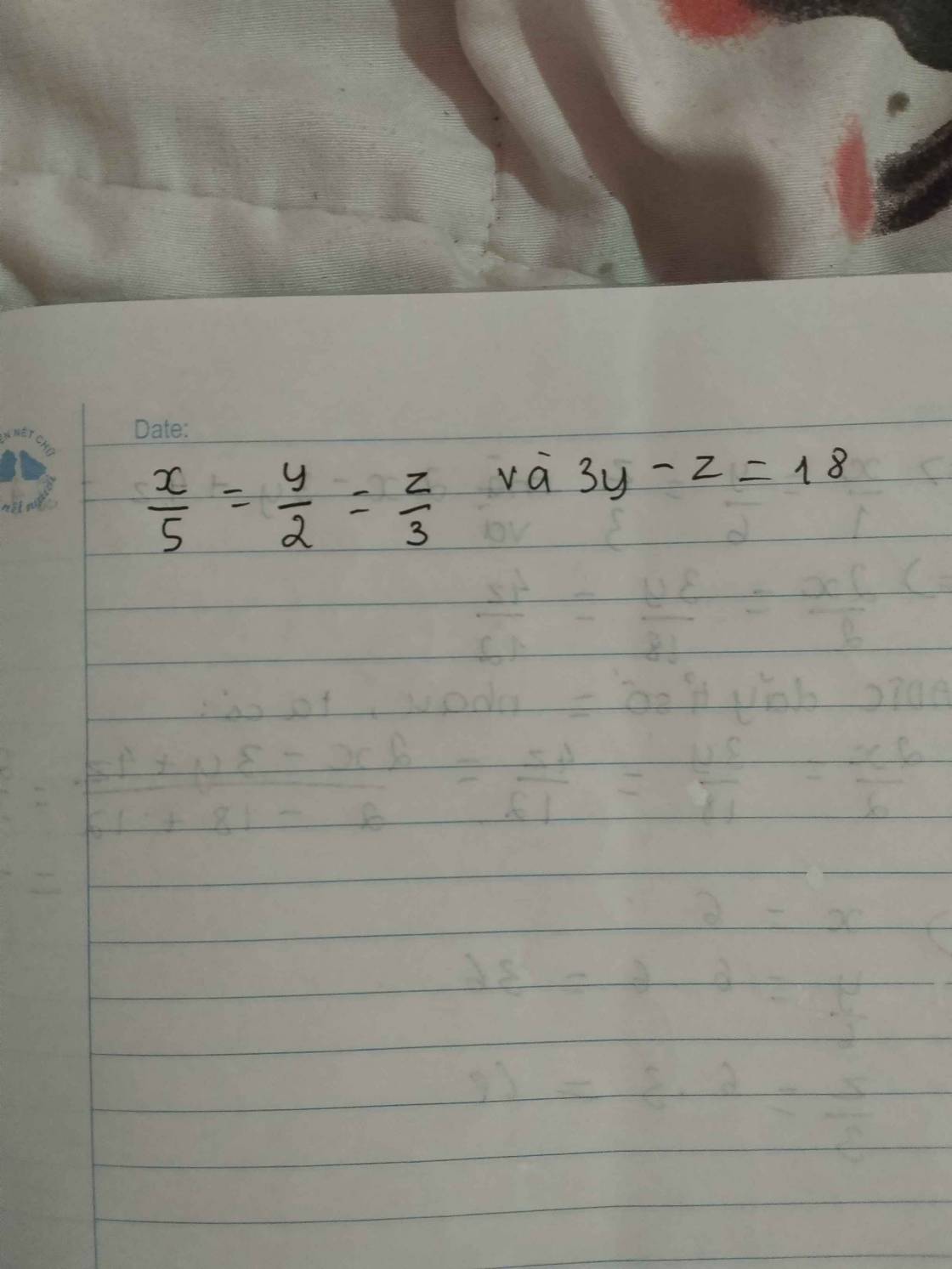Đặt \(\dfrac{a}{b}\)= \(\dfrac{c}{d}\)= k  <=> \(\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)

\(VT:\dfrac{7a^2+3ab}{11a^2-8b^2}=\dfrac{7b^2k^2+3b^2k}{11b^2k^2-8b^2}=\dfrac{b^2\left(7k^2+3k\right)}{b^2\left(11k^2-8\right)}\)\(=\dfrac{7k^2+3k}{11k^2-8}\)

\(VP:\dfrac{7c^2+3cd}{11c^2-8d^2}=\dfrac{7d^2k^2+3d^2k}{11d^2k^2-8d^2}=\dfrac{d^2\left(7k^2+3k\right)}{d^2\left(11k^2-8\right)}=\dfrac{7k^2+3k}{11k^28}\)

⇒VT=VP

⇒đpcm

-12phần5

\(\dfrac{3}{5}=0,6\)                 1\(\dfrac{1}{4}\) = 1,25 

gọi 3 phần của số 106 lần lượt là x; y; z 

theo bài ra ta có : 

\(\dfrac{x}{0,6}\)= \(\dfrac{y}{1,25}\) = \(\dfrac{z}{0,8}\)

áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\dfrac{x}{0,6}\) = \(\dfrac{y}{1,25}\)= \(\dfrac{z}{0,8}\) = \(\dfrac{x+y+z}{0,6+1,25+0,8}\) = \(\dfrac{106}{2,65}\) = 40

\(x=40.0,6=24\) ;  y = 40.1,25 = 50;    z = 40.0,8 = 32

vậy 106 được chia thành 3 phần là 24; 50; 32 

Lời giải:

1.

$(x+\frac{1}{2})^2=25=5^2=(-5)^2$

$\Rightarrow x+\frac{1}{2}=5$ hoặc $x+\frac{1}{2}=-5$

$\Rightarrow x=\frac{9}{2}$ hoặc $x=\frac{-11}{2}$

2.

$2^{x-1}=16=2^4$

$\Rightarrow x-1=4$

$\Rightarrow x=5$

3.

$6x=10y=15z$

$\Rightarrow \frac{6x}{30}=\frac{10y}{30}=\frac{15z}{30}$

$\Rightarrow \frac{x}{5}=\frac{y}{3}=\frac{z}{2}$

$=\frac{x+y+z}{5+3+2}=\frac{90}{10}=9$

$\Rightarrow x=5.9=45; y=3.9=27; z=2.9=18$

Lời giải:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\frac{x}{5}=\frac{y}{2}=\frac{z}{3}=\frac{3y}{6}=\frac{z}{3}$

$=\frac{3y-z}{6-3}=\frac{18}{3}=6$

$\Rightarrow x=5.6=30; y=2.6=12; z=3.6=18$ 

Vậy..........

Lời giải:

Đặt $\frac{a}{b}=\frac{c}{d}=k$
$\Rightarrow a=bk; c=dk$. Khi đó:
$\frac{5a+3b}{5a-3b}=\frac{5bk+3b}{5bk-3b}=\frac{b(5k+3)}{b(5k-3)}=\frac{5k+3}{5k-3}(1)$
$\frac{5c+3d}{5c-3d}=\frac{5dk+3d}{5dk-3d}=\frac{d(5k+3)}{d(5k-3)}=\frac{5k+3}{5k-3}(2)$

Từ $(1); (2)\Rightarrow \frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}$
b. Bạn làm tương tự. Thay $a=bk; c=dk$ vào rồi rút gọn thôi.