giúp mình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


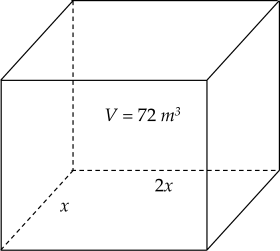
Diện tích đáy bể là: \(2x^2\) `(m^2)`
Chiều cao bể là: \(\dfrac{72}{2x^2}=\dfrac{36}{x^2}\left(m^2\right)\)
Diện tích xung quanh bể là: \(\left(2x+x\right).2.\dfrac{36}{x^2}=\dfrac{216}{x}\left(m^2\right)\)
Diện tích cần xây là:
\(2x^2+\dfrac{216}{x}=2\left(x^2+\dfrac{54}{x}+\dfrac{54}{x}\right)\ge2.3\sqrt[3]{x^2.\dfrac{54}{x}.\dfrac{54}{x}}=54\sqrt[3]{4}\left(m^2\right)\)
Dấu "=" xảy ra khi \(x^2=\dfrac{54}{x}\Rightarrow x=\sqrt[3]{54}=3,78\left(m\right)\)

a: Ta có: AM\(\perp\)AB
BP\(\perp\)AB
Do đó: AM//BP
Xet ΔOAM vuông tại A và ΔOBP vuông tại B có
OA=OB
\(\widehat{AOM}=\widehat{BOP}\)(hai góc đối đỉnh)
Do đó: ΔOAM=ΔOBP
=>OM=OP
b: Xét ΔNOM vuông tại O và ΔNOP vuông tại O có
NO chung
OM=OP
Do đó: ΔNOM=ΔNOP
=>\(\widehat{NMO}=\widehat{NPO}\)
=>\(\widehat{NMO}=\widehat{AMO}\)
=>MO là phân giác của góc AMN
Xét ΔMAO vuông tại A và ΔMHO vuông tại H có
MO chung
\(\widehat{AMO}=\widehat{HMO}\)
Do đó: ΔMAO=ΔMHO
=>OA=OH
=>OH=R
Xét (O) có
OH là bán kính
MN\(\perp\)OH tại H
Do đó: MN là tiếp tuyến của (O)
Xét (O) có
NH,NB là các tiếp tuyến
Do đó: NH=NB
ΔMAO=ΔMHO
=>MA=MH
Xét ΔOMN vuông tại O có OH là đường cao
nên \(HM\cdot HN=OH^2=R^2\)
=>\(MA\cdot BN=R^2\)

a: Ta có: ΔOBD cân tại O
mà OA là đường cao
nên OA là phân giác của góc BOD
Xét ΔOBA và ΔODA có
OB=OD
\(\widehat{BOA}=\widehat{DOA}\)
OA chung
Do đó: ΔOBA=ΔODA
=>\(\widehat{OBA}=\widehat{ODA}\)
=>\(\widehat{ODA}=90^0\)
=>AD là tiếp tuyến của (O)
Xét (O) có
ΔBDE nội tiếp
BE là đường kính
Do đó: ΔBDE vuông tại D
=>BD\(\perp\)DE
mà BD\(\perp\)OA
nên OA//DE
b: Xét (O) có
ΔBFE nội tiếp
BE là đường kính
Do đó: ΔBFE vuông tại F
=>BF\(\perp\)AE tại F
Xét ΔBEA vuông tại B có BF là đường cao
nên \(AF\cdot AE=AB^2\left(1\right)\)
Xét ΔABO vuông tại B có BC là đường cao
nên \(AC\cdot AO=AB^2\left(2\right)\)
Từ (1),(2) suy ra \(AF\cdot AE=AC\cdot AO\)

Diện tích mảnh vườn là:
25x10:2=125(m2)
Số tiền cần dùng là
55000x125=6875000(đồng)
Diện tích mảnh vườn là:
\(25\times10:2=125\left(m^2\right)\)
Số tiền cần để mua cỏ là:
\(125\times55000=6875000\) (đồng)

a: 0,25x92,6x40
=40x0,25x92,6
=92,6x10
=926
b: 97,1x0,01+102,9x0,01
=0,01x(97,1+102,9)
=0,01x200
=2
Trả lời:
a) 0,25 × 92,6 × 40 b) 97,1 × 0,01 + 102,9 × 0,01
=(0,25 x 40) x 92,6 =(102,9+97,1) x 0,01
=10 x 92,6 =200 x 0,01
=926 =2


a: \(317ha=3,17km^2\)
b: 67ml=0,067 lít
c: 9 yến 5kg=9,5 yến
d: 9m17cm=9,17m
Trả lời:
a) 317 ha =3,17 km2
b) 67 ml =0,067 l
c) 9 yến 5 kg =9,5 yến
d) 9 m 17 cm =9,17 m

Số tiền giảm đi:
\(15750000\times10\%=1575000\) (đồng)
Giá bán của chiếc máy tính sau khi giảm giá:
\(15750000-1575000=14175000\) (đồng)

a) \(0,125\times7,21\times80\)
\(=\left(0,125\times80\right)\times7,21\)
\(=10\times7,21\)
\(=72,1\)
b) \(7,3\times0,001+92,7\times0,001\)
\(=0,001\times\left(7,3+92,7\right)\)
\(=0,001\times100\)
\(=0,1\)

Câu 3.1
+ Vì p; q đều là số nguyên tố nên p.q > 2 mà pq + 11 là số nguyên tố nên pq + 11 là số lẻ.
+ Vì 11 là số lẻ thì pq là số chẵn. Vậy p, q phải có ít nhất một số là số chẵn.
a; Nếu p = 2 ta có: 14 + q \(\in\) P và 2q + 11 \(\in\) P
+ Nếu q = 2 ta có: 14 + 2 = 16 (loại vì 16 không phải là số nguyên tố)
+ Nếu q = 3 ta có: \(\left\{{}\begin{matrix}14+q=14+3=17\left(tm\right)\\2.q+11=2.3+11=17\left(tm\right)\end{matrix}\right.\)
+ Nếu q > 3 thì q có dạng: q = 3k + 1 hoặc 3k + 2
Trường hợp 1: q = 3k + 1 thì
14 + q = 14 + 3k + 1 = (14 + 1) + 3k = 15 + 3k ⋮ 3 (loại vì đây là hợp số)
Trường hợp 2: q = 3k + 2 thì:
2q + 11 = 2.(3k + 2) + 11 = 6k + 4 +11 = 6k + (4 + 11) = 6k + 15 ⋮ 3(loại vì đây là hợp số)
b; Nếu q = 2 ta có: 7p + 2 \(\in\) P và 2p + 11 \(\in\) P
Chứng minh tương tự ta có: q = 2 và p = 3
Từ những lập luận và phân tích trên ta có các cặp số nguyên tố p và q thỏa mãn đề bài là:
(p; q) = (2; 3); (3; 2)
Câu 4:
Gọi chiều rộng khu đất là x(m)
(Điều kiện: x>0)
Chiều dài khu đất là 3x(m)
Chiều rộng khu đất sau khi tăng thêm 3m là x+3(m)
Chiều dài khu đất sau khi giảm đi 3m là 3x-3(m)
Diện tích tăng thêm 75m2 nên ta có:
\(\left(3x-3\right)\left(x+3\right)-3x\cdot x=75\)
=>\(3x^2+9x-3x-9-3x^2=75\)
=>6x=9+75=84
=>x=14(nhận)
Vậy: Chiều rộng khu đất là 14m
Chiều dài khu đất là 14*3=42m
Câu 4: Số học sinh khối 6 tham dự là:
\(250\cdot40\%=100\left(bạn\right)\)
Tổng số học sinh khối 7 và khối 8 tham dự là:
250-100=150(bạn)
Tỉ số giữa số học sinh khối 7 và khối 8 là:
\(\dfrac{4}{7}:\dfrac{1}{2}=\dfrac{8}{7}\)
Số học sinh khối 7 tham dự là:
\(150\cdot\dfrac{8}{7+8}=150\cdot\dfrac{8}{15}=80\left(bạn\right)\)
Số học sinh khối 8 tham dự là:
150-80=70(bạn)