Cho hai điểm A, B vẽ đường thẳng m vuông góc với đoạn thẳng AB tại điểm A. Lấy điểm M thuộc đường thẳng m, trên tia đối của tia AM lấy điểm N sao cho AM = AN. Qua N kẻ đường thẳng vuông góc với MB cắt AB tại H.
a) Chứng minh MH vuông góc với NC.
b) Chứng minh tam giác BMN cân tại B.
Ai bt làm bài này ko, giúp mình với. Khó quá

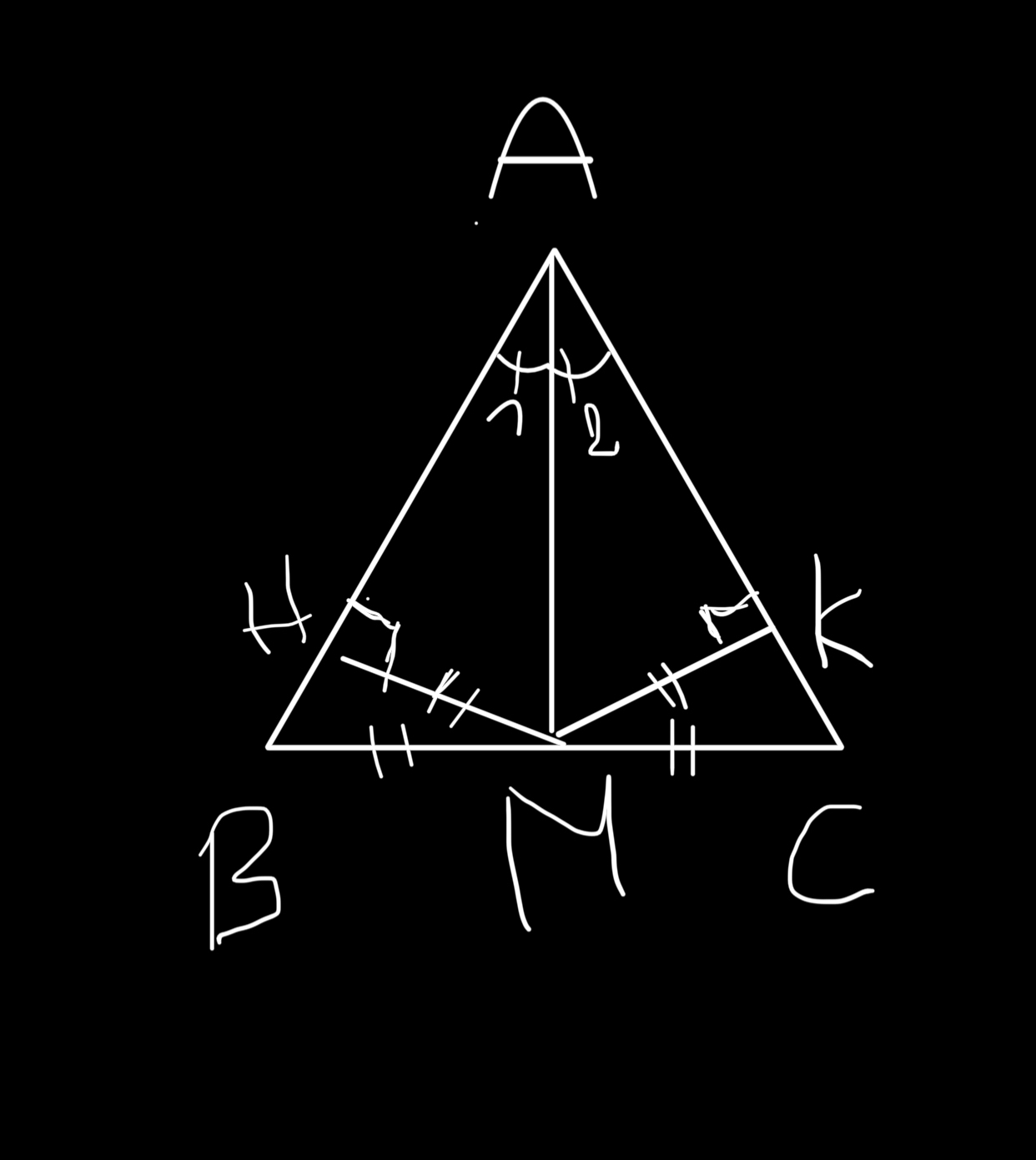
điểm c ở đâu ra v bn hả
ko cs đ C thì lm kiểu j bn hả