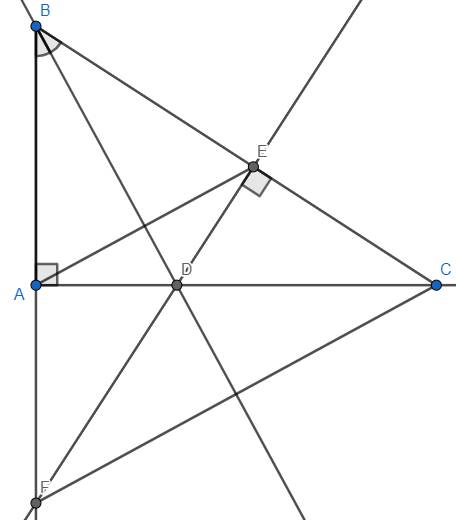
Cho \(\Delta\)MNP có 3 góc nhọn,các đường cao NQ,PR cắt nhau tại S
a)Chứng minh MS\(\perp\)NP
b)Cho góc MNP=65 độ tính góc SMR
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thể tích hình hộp chữ nhật làm bằng bìa là:
22 x 16 x 18 = 6336 (cm3)
Đáp số: 6336cm3
Hình khối chỉ có DT toàn phần và xung quanh thôi.

c) Ta đã biết DA = DE (chứng minh trên) (1)
Trong tam giác EDC vuông tại E có DC đối diện đỉnh E
Suy ra DC là cạnh lớn nhất trong tam giác EDC
Hay DC > DE (2)
Từ (1) và (2) suy ra DC > AD hay AD < DC
ÉT Ô ÉT
Câu 3: Tìm x biết:
|x + 1| + |x + 2| + |x + 2020| = 4x
Giúp mik với!!!
Mik hứa Tick cho… Pls

TH1 : \(x< -2020\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = - ( x + 1 ) - ( x + 2 ) - ( x + 2020 ) = 4x
<=> -3x - 2023 = 4x <=> -7x = 2023 <=> x = -289
TH2 : \(-2020\le x< -2\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = - ( x + 1 ) - ( x + 2 ) + x + 2020 = 4x
<=> -x + 2017 = 4x
<=> -5x = -2017 <=> x = 2017/5 ( = 403,4 )
TH3 : \(-2\le x< -1\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = - ( x + 1 ) + x + 2 + x + 2020 = 4x
<=> x + 2021 = 4x <=> -3x = -2021 <=> x = 2021/3
TH4 : \(x>-1\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = x + 1 + x + 2 + x + 2020 = 4x
<=> 3x + 2023 = 4x
<=> -x = -2023 <=> x = 2023
Vậy...
TH1: x ≥ 0
Khi đó \(\left|x+1\right|+\left|x+2\right|+\left|x+2020\right|=x+1+x+2+x+2020\)
\(=3x+2023=4x\)
Suy ra \(4x-3x=x=2023\) (thỏa mãn điều kiện)
TH2: x < 0
Khi đó 4x < 0 hay vế phải luôn là một số âm. Tuy nhiên vế trái luôn luôn có giá trị lớn hơn 0 nên luôn là 0 hoặc là một số dương, suy ra vô lí.
Tóm lại, x = 2023.

Độ dài cạnh của hình vuông:
\(36,8:4=9,2\left(cm\right)\)
Đáp số: 9,2 cm

Gọi X là tập hợp các kết quả có thể xảy ra.
Ta có \(X=\left\{\left(1;1\right);\left(1;2\right);\left(1;3\right);...;\left(6;6\right)\right\}\). Ta thấy tập hợp trên có 36 phần tử, hoặc 36 kết quả có thể xảy ra.
a) Biến cố trên có thể xảy ra nếu xảy ra 1 trong các kết quả sau:
(4;6); (5;5); (6;4). Có 3 kết quả để biến cố trên xảy ra.
Vậy xác suất của biến cố trên là \(\dfrac{3}{36}=\dfrac{1}{12}\).
b) Biến cố trên có thể xảy ra nếu xảy ra 1 trong các kết quả sau:
(1;2); (2;1); (1;4); (2;3); (3;2); (4;1); (1;6); (2;5); (3;4); (4;3); (5;2); (6;1); (3;6); (4;5); (5;4); (6;3); (5;6); (6;5). Có 18 kết quả để biến cố trên xảy ra.
Vậy xác suất để biến cố trên xảy ra là \(\dfrac{18}{36}=\dfrac{1}{2}\).
a) Theo đề ta có S là trực tâm của tam giác MNP và MNP là tam giác nhọn
Suy ra MS cũng là đường cao đáy NP, hay \(MS\perp NP\)
b) Gọi O là giao điểm của MS và NP. Ta có MNO là tam giác vuông tại O
Suy ra \(\widehat{MNO}+\widehat{NMO}=90^o\) hay \(\widehat{MNP}+\widehat{SMR}=90^o\)
Suy ra \(\widehat{SMR}=90^o-\widehat{MNP}=90^o-65^o=25^o\)