a, dễ tự làm 

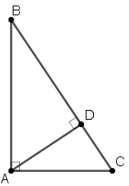
b, xét tam giác CAB và tam giác DAB có : AB chung

AC = AD (gt)

góc CAB = góc DAB = 90

=> tam giác CAB = tam giác DAB (2cgv) 

=> góc CBA = góc DBA (đn)

xét tam giác AFB và tam giác AEB có : AB chung

góc AFB = góc AEB = 90

=>  tam giác AFB = tam giác AEB (ch - gn)

\(3x=2y\Rightarrow\frac{x}{2}=\frac{y}{3}\)

\(5x=2z\Rightarrow\frac{x}{2}=\frac{z}{5}\)

\(\Rightarrow\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\)

Đặt \(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=k\)

\(\Rightarrow x=2k;y=3k;z=5k\)

\(\Rightarrow\left(2k\right)^3+\left(3k\right)^3-2k\cdot3k\cdot5k=40\)

\(\Rightarrow k^3\cdot8+k^3\cdot27-k^3\cdot30=40\)

\(\Rightarrow k^3\left(8+27-30\right)=40\)

\(\Rightarrow k^3=8\)

\(\Rightarrow k=2\)

\(\Rightarrow\hept{\begin{cases}x=2\cdot2=4\\y=2\cdot3=6\\z=2\cdot5=10\end{cases}}\)

Có 

Dấu "=" ko xảy ra 

Nè sai đề phải k PK vuông góc vs chứ ko phải PH là 1

I đâu ra mà c/m hai góc đó là 2  nêu đề /m HPB và KPC thì làm đc

Nếu đề sai thì viết vào dưới bài này mình sẽ giải cho

đúng rồi pk

Hình vẽ : 

Chứng minh :

Giả sử \(\triangle ABC\) có AD là đường trung tuyến ứng với BC và \(DA=\frac{1}{2}BC\).

\(\Rightarrow AD=BD=CD\)

\(+AD=BC\Rightarrow\triangle ADC\text{ cân tại D}\)

\(\Rightarrow\widehat{A_1}=\widehat{C}\)

\(+AD=BD\Rightarrow\triangle ABD\text{ cân tại D}\)

\(\Rightarrow\widehat{A_2}=\widehat{B}\)

\(\Rightarrow\widehat{A_1}+\widehat{A_2}=\widehat{B}+\widehat{C}\)

\(\Rightarrow\widehat{A}=\widehat{B}+\widehat{C}\)

Trong \(\triangle ABC\) có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)

\(\Rightarrow\widehat{A}=\widehat{B}+\widehat{C}=\frac{180^0}{2}=90^0\)

hay \(\triangle ABC\) vuông tại A (đpcm)

Hình như câu d sai đề

Bạn tự vẽ hình nha

a) xét ∆NAD và ∆NBD có

        ND cạnh chung

     AD=AB   (d là trung điểm của AB )

      Góc NDA = góc NDB(=90°)

=>∆NAD=∆NBD(C-G-C)

b) xét ∆MNA và ∆MNB có

       MN cạnh chung

     Góc MNA = góc MNB (vì ∆NAD=∆NBD )

       NA =NB (vì ∆NAD=∆NBD)

=>∆MNA=∆MNB(c-g-c)

c) ta có ∆NAD=∆NBD (cmt)

 =>góc AND =góc BND (2 GÓC TƯƠNG ỨNG )

 =>ND LÀ TIA PHÂN GIÁC CỦA GÓC ANB

a) Xét tam giác AMB và AMC có:

AM chung 

AB=AC (tam giác ABC cân tại A)

\(\widehat{A_1}=\widehat{A_2}\)(AM là phân giác)
=> \(\Delta AMB=\Delta AMC\left(cgc\right)\)(đpcm)

b) Có tam giác ABC cân tại A (gt); AM là trung tuyến tam giác ABC

Vì trong tam giác cân đường trung tuyến trùng với đường cao

=> AM là đường cao tam giác ABC 

=> AM _|_ BC (đpcm)

Bài làm

a) Xét tam giác AMB và tam giác AMC có:

^MAB = ^MAC ( Do AM phân giác )

AB = AC ( Do ∆ABC cân )

^B = ^C ( Do ∆ABC cân )

=> ∆AMB = ∆AMC ( g.c.g )

b) Cách 1: Vì ∆AMB = ∆AMC ( cmt )

=> ^AMB = ^AMC 

Mà ^AMB + ^AMC = 180° ( hai góc kề bù )

=> ^AMB = ^AMC = 180°/2 = 90°

=. AM vuông góc với BC.

Cách 2: Vì tam giác ABC cân tại A

Mà AM là tia phân giác

=> AM đồng thời là đường cao.

=> AM vuông góc với BC .

c) Vì ∆ABC cân tại A

Mà AM vừa là đường phân giác, vừa là đường cao.

=> AM là đường trung tuyến. 

=> BM = MC 

Mà BM + MC = BC = 6

=> BM = MC = 6/2 = 3 ( cm )

Xét tam giác AMB vuông tại M có:

Theo định lí Pytago có:

AB² = AM² + BM²

=> AM² = AB² - BM²

Hay AM² = 5² - 3²

=> AM² = 25 - 9

=> AM² = 16

=> AM = 4 ( cm )

d) Xét tam giác ABC có:

AM vuông góc với BC

AH vuông góc với AC

Mà AM cắt AH tại H

=> H là trực tâm.

=> CH vuông góc với AB . ( Đpcm )

+ TH1: Xét ΔABC vuông tại A có các đường cao AD, BA, CA.

BA, CA là hai đường cao xuất phát từ hai góc nhọn B và C của ΔABC.

AB = AC ⇒ ΔABC cân tại A (đpcm).

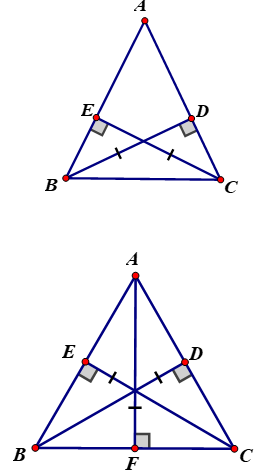
+ TH2: Xét ΔABC không có góc nào vuông, hai đường cao BD = CE (như hình vẽ minh họa)

Xét hai tam giác vuông EBC và DCB có :

BC (cạnh chung)

CE = BD (giả thiết)

⇒ ∆EBC = ∆DCB (cạnh huyền - cạnh góc vuông)

+ Xét ΔABC ba đường cao BD = CE = AF (như hình vẽ minh họa)

CE = BD ⇒ ΔABC cân tại A (như cmt) ⇒ AB = AC.

CE = AF ⇒ ΔABC cân tại B (như cmt) ⇒ AB = BC:

⇒ AB = AC = BC

⇒ ΔABC đều.