1243+18239:7=may
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\dfrac{100}{1\cdot2}+\dfrac{100}{2\cdot3}+\dfrac{100}{3\cdot4}+...+\dfrac{100}{99\cdot100}\)
\(A=100\cdot\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{99\cdot100}\right)\)
\(A=100\cdot\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(A=100\cdot\left(1-\dfrac{1}{100}\right)\)
\(A=100\cdot\dfrac{99}{100}\)
A=99

1, \(\dfrac{-1}{2}+\dfrac{-1}{3}-\dfrac{-5}{4}\)
\(=\dfrac{-6}{12}+\dfrac{-4}{12}+\dfrac{15}{12}=\dfrac{5}{12}\)
2, \(\dfrac{5}{4}-\dfrac{1}{2}+\dfrac{-7}{8}\)
\(=\dfrac{10}{8}-\dfrac{4}{8}+-\dfrac{7}{8}=\dfrac{-1}{8}\)
3, \(\dfrac{1}{5}-\dfrac{1}{2}+\dfrac{9}{10}\)
\(=\dfrac{2}{10}-\dfrac{5}{10}+\dfrac{9}{10}=\dfrac{6}{10}=\dfrac{3}{5}\)
4, \(\dfrac{5}{4}-\dfrac{1}{2}+\dfrac{7}{6}\)
\(=\dfrac{15}{12}-\dfrac{6}{12}+\dfrac{14}{12}=\dfrac{23}{12}\)
5, \(\dfrac{-2}{5}+\dfrac{-7}{10}-\dfrac{9}{6}\)
\(=\dfrac{-12}{30}+\dfrac{-21}{30}-\dfrac{45}{30}=\dfrac{-78}{30}=\dfrac{-13}{5}\)
6, \(\dfrac{1}{2}+\dfrac{-2}{5}-\dfrac{-2}{3}\)
\(=\dfrac{15}{30}+\dfrac{-12}{30}+\dfrac{20}{30}=\dfrac{23}{30}\)
7, \(\dfrac{5}{3}-\dfrac{3}{4}+\dfrac{7}{6}\)
\(=\dfrac{20}{12}-\dfrac{9}{12}+\dfrac{14}{12}=\dfrac{25}{12}\)
8, \(\dfrac{-1}{5}+\dfrac{5}{3}-\dfrac{3}{2}\)
\(=\dfrac{-6}{30}+\dfrac{50}{30}-\dfrac{45}{30}=\dfrac{-1}{30}\)
9, \(\dfrac{1}{4}-\dfrac{7}{8}+\dfrac{-9}{10}\)
\(=\dfrac{10}{40}-\dfrac{35}{40}+\dfrac{-36}{40}=\dfrac{-61}{40}\)
10, \(\dfrac{5}{4}+\dfrac{1}{2}+\dfrac{-7}{12}\)
\(=\dfrac{15}{12}+\dfrac{6}{12}+\dfrac{-7}{12}=\dfrac{14}{12}=\dfrac{7}{6}\)
11, \(\dfrac{-5}{8}-\dfrac{1}{3}+\dfrac{-7}{6}\)
\(=\dfrac{-15}{24}-\dfrac{8}{24}+\dfrac{-28}{24}=\dfrac{-51}{24}=\dfrac{-17}{8}\)
12, \(\dfrac{-3}{4}-\dfrac{7}{10}+\dfrac{-5}{6}\)
\(=\dfrac{-45}{60}-\dfrac{42}{60}+\dfrac{-50}{60}=\dfrac{-137}{60}\)
\(#WendyDang\)
\(#NqHahh\)

a; \(\dfrac{x}{8}\) = \(\dfrac{3}{4}\) + \(\dfrac{-5}{8}\)
\(\dfrac{x}{8}\) = \(\dfrac{1}{8}\)
\(x\) = \(\dfrac{1}{8}\) \(\times\) 8
\(x\) = 1
b; \(\dfrac{x}{12}\) = \(\dfrac{3}{4}\) + \(\dfrac{-2}{3}\)
\(\dfrac{x}{12}\) = \(\dfrac{1}{12}\)
\(x\) = \(\dfrac{1}{12}\) \(\times\) 12
\(x\) = 1
c; 1 + \(\dfrac{11}{3}\) = \(\dfrac{24}{x}\)
\(\dfrac{14}{3}\) = \(\dfrac{24}{x}\)
\(x\) = 24 : \(\dfrac{14}{3}\)
\(x\) = \(\dfrac{36}{7}\)
d; \(\dfrac{x}{6}\) - \(\dfrac{3}{4}\) = \(\dfrac{1}{12}\)
\(\dfrac{x}{6}\) = \(\dfrac{1}{12}\) + \(\dfrac{3}{4}\)
\(\dfrac{x}{6}\) = \(\dfrac{5}{6}\)
\(x\) = \(\dfrac{5}{6}\) \(\times\) 6
\(x\) = 5

\(A=1+2-3-4+5+6-7-8+...-2020\)
\(A=\left(1+2-3-4\right)+\left(5+6-7-8\right)+...+\left(2017+2018-2019-2020\right)\)
\(A=\left(-4\right)+\left(-4\right)+...+\left(-4\right)\)
\(A=\left(-4\right)\cdot\dfrac{2020}{4}\)
\(A=-2020\)
A=1+2-3-4+5+6-7-8+9+..+2018-2019-2020
A= (1+2-3-4) + (5+6-7-8) +...+ (2017+2018 - 2019 - 2020)
A= -4 + (-4) +... + (-4) (505 thừa số -4)
A= -4 x 505 = -2020

đk (\(x\); y \(\in\) Z; y ≠ -1)
\(\dfrac{x}{3}\) - \(\dfrac{1}{y+1}\) = \(\dfrac{1}{6}\)
\(\dfrac{xy+x-3}{3.\left(y+1\right)}\) = \(\dfrac{1}{6}\)
\(\dfrac{xy+x-3}{y+1}\) = \(\dfrac{1}{6}\) \(\times\) 3
\(\dfrac{xy+x-3}{y+1}\) = \(\dfrac{1}{2}\)
2.(\(xy+x-3\)) = y + 1
2\(xy\) + 2\(x\) - 6 = y + 1
2\(xy\) - y + 2\(x\) - 1 = 5 + 1
y.(2\(x\) - 1) + (2\(x\) - 1) = 6
(2\(x\) - 1).(y + 1) = 6
6 = 6; Ư(6) = {-6; -3; -2; -1; 1; 2; 3; 6}
Lập bảng ta có:
| y + 1 | -6 | -3 | -2 | -1 | 1 | 2 | 3 | 6 |
| y | -7 | -4 | -3 | -2 | 0 | 1 | 2 | 5 |
| 2\(x-1\) | -1 | -2 | -3 | -6 | 6 | 3 | 2 | 1 |
| \(x\) | 0 | -1/2 | -1 | -5/2 | 7/2 | 2 | 3/2 | 1 |
Theo bảng trên ta có các cặp (\(x;y\)) nguyên thỏa mãn đề bài là:
(\(x\); y) = (0; -7); (-1; -3); (2; 1); (1; 5)

a; \(\dfrac{x-1}{12}\) = \(\dfrac{5}{3}\)
\(x-1\) = \(\dfrac{5}{3}\) \(\times\) 12
\(x\) - 1 = 20
\(x\) = 20 + 1
\(x\) = 21
b; \(\dfrac{-x}{8}\) = \(\dfrac{-50}{x}\)
-\(x\).\(x\) = -50.8
-\(x^2\) = -400
\(x^2\) = 400
\(\left[{}\begin{matrix}x=-20\\x=20\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-20; 20}
c; \(\dfrac{x}{3}\) = \(\dfrac{14}{x+1}\)
\(x\).(\(x\)+1) = 14.3
\(x^2\) + \(x\) = 42
\(x^2\) + \(x\) - 42 = 0
\(x^2\) - 6\(x\) + 7\(x\) - 42 = 0
\(x\).(\(x\) - 6) + 7.(\(x\) - 6) = 0
(\(x\) - 6).(\(x\) + 7) = 0
\(\left[{}\begin{matrix}x-6=0\\x+7=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=6\\x=-7\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-7; 6}
d; \(x-\dfrac{2}{9}\) = \(\dfrac{1}{6}\)
\(x\) = \(\dfrac{1}{6}\) + \(\dfrac{2}{9}\)
\(x\) = \(\dfrac{7}{18}\)
Vậy \(x\) = \(\dfrac{7}{18}\)

\(\dfrac{-5}{18}+\dfrac{5}{12}=\dfrac{-10}{36}+\dfrac{15}{36}=\dfrac{5}{36}\)

\(\left|2x-1\right|=16\)
\(\Rightarrow\) Ta có: \(\left\{{}\begin{matrix}2x-1=16\\2x-1=-16\end{matrix}\right.\)
\(\left\{{}\begin{matrix}2x=16+1\\2x=-16+1\end{matrix}\right.\)
\(\left\{{}\begin{matrix}2x=17\\2x=-15\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x=17:2\\x=-15:2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{17}{2}\\x=\dfrac{-15}{2}\end{matrix}\right.\)
\(\Rightarrow x\in\left\{{}\begin{matrix}\dfrac{17}{2}\\\dfrac{-15}{2}\end{matrix}\right.\)
|2\(x\) - 1| = 16
\(\left[{}\begin{matrix}2x-1=16\\2x-1=-16\end{matrix}\right.\)
\(\left[{}\begin{matrix}2x=17\\2x=-15\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{17}{2}\\x=-\dfrac{15}{2}\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-\(\dfrac{15}{2}\); \(\dfrac{17}{2}\)}
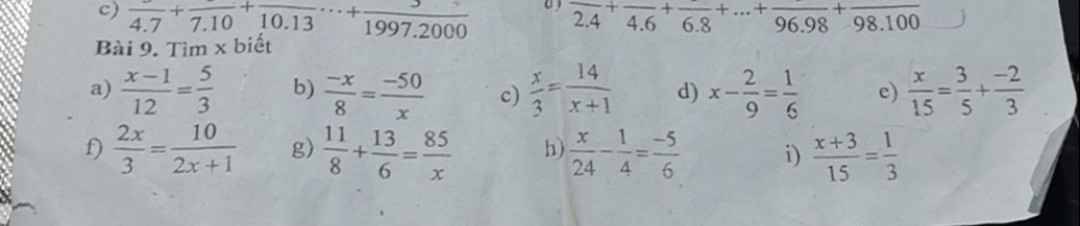
\(\dfrac{26940}{7}\)
1 243 + 18 239: 7
= 1 243 + 2 605.4
= 3 848.4